 |
Главная |
Великая теорема Ферма. Решение
|
из
5.00
|
Алгоритм решения Диофантовых уравнений
Нижнегородская область
Г.Заволжье
2009 г.
В работе рассмотрен метод исследования Диофантовых уравнений и представлены решенные этим методом:
- великая теорема Ферма;
- уравнение Пелля;
- уравнения эллиптических кривых У2=X3+K,
(У2=Х3-Х, У2=Х3-Х+1, У2=Х3+аХ+В);
- иррациональные корни уравнения Х2-У2=1;
- поиск Пифагоровых троек;
- уравнение Каталана;
- уравнение гипотезы Билля
Решение Диофантовых уравнений
Лирическое отступление (ЛО) – 1
Всё началось с теоремы Ферма.
В клубе фермистов оказался случайно, решал совершенно другую задачу, и неожиданно пришла идея ВТФ. Я даже не помнил её классическое написание – хn+уn=сn , формулу ВТФ написал в виде хn = уn + сn, а потом не стал переучиваться, т.к. привык к своему написанию формулы.
ЛО – 2. При доказательстве ссылаюсь на закон распределения простых чисел. Можно было бы обойтись без упоминания оного. Просто сохранил историческую правду, т.к. лично для меня этот закон стал подсказкой.
ЛО – 3. Этот же подход был применён для решения уравнения гипотезы Биля и решения других уравнений. Выводы получились интересными.
Для себя обкатал этот метод на нескольких шуточных уравнениях. При профессиональном подходе, похоже, этот метод может дать как качественные выводы, так и количественные, окончательный же приговор этому методу будет сделан совместными усилиями.
Великая теорема Ферма. Решение
 – не имеет решений в целых числах при показателе степени n>2.
– не имеет решений в целых числах при показателе степени n>2.
Для доказательства данного утверждения было рассмотрено аналогичное функциональное уравнение. Чтобы получить функциональное уравнение надо обратиться к закону распределения простых чисел в ряду натуральных чисел. В таблице изображена матрица распределения составных чисел в ряду натуральных чисел.
 |  | ||||
 | |||||
| 4 |
| 6 |
| 8 |
| 10 |
| 12 |
| 14 |  +2 +2
| 16 |  +2 +2
| 18 | … | ||||||
|
+2 |
|
+3 |
|
+4 |
|
+5 |
|
+6 |
|
+7 |  +8
+8
|  +9
+9
| |||||||||
| 6 |
| 9 |
| 12 |
| 15 |
| 18 |
| 21 |  +3 +3
| 24 |  +3 +3
| 27 | … | ||||||

|
|
|
|
|
|
|
|
|
|
| |||||||||||
| 8 | +4
| 12 |
| 16 |
| 20 |
| 24 |
| 28 | 32 | 36 | … | ||||||||
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||
| 10 |
| 15 |
| 20 |
| 25 |
| 30 |
| 35 | 40 | 45 | … | ||||||||

|
|
|
|
|
|
|
|
|
|
| |||||||||||
| 12 | +6 | 18 |
| 24 |
| 30 |
| 36 |
| 42 | 48 | 54 | … | ||||||||
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||
| 14 |
| 21 |
| 28 |
| 35 |
| 42 |
| 49 | 56 | 63 | … | ||||||||
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||
| 16 |
| 24 |
| 32 |
| 40 |
| 48 |
| 56 | 64 | 72 | … | ||||||||
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||
| 18 |
| 27 |
| 36 |
| 45 |
| 54 |
| 63 | 72 | 81 | … | ||||||||
| … |
| … |
| … |
| … |
| … |
| … | … | … |
Формула любого составного числа, соответствующего этой матрице, имеет вид - (  i + 1) (
i + 1) (  j + 1), где
j + 1), где  i - номер столбца этой матрицы,
i - номер столбца этой матрицы,
 j – соответственно, номер строки этой матрицы. Для верхней строки (
j – соответственно, номер строки этой матрицы. Для верхней строки (  = 1) формула составного числа примет вид – 2(
= 1) формула составного числа примет вид – 2(  i + 1) – это ряд чётных чисел.
i + 1) – это ряд чётных чисел.
Всё это пока заготовка для доказательства великой теоремы Ферма (ВТФ).
Нечётные числа примут вид 2(  i + 1) ± 1. В нашем случае пусть нечётные числа будут - 2(
i + 1) ± 1. В нашем случае пусть нечётные числа будут - 2(  i + 1) - 1.
i + 1) - 1.
Чтобы доказать ВТФ надо рассмотреть три варианта:
- I X - чётное число, У - чётное число, Z - чётное число;
- II X - чётное число, У - нечётное число, Z - нечётное число;
- III X - нечётное число, У - чётное число, Z - нечётное число.
Вариант I. Пусть уравнение ВТФ верно для чётных чисел.
В формулу ВТФ вставим аналитические выражения чётных чисел.
[2(  1 + 1)]n = [2(
1 + 1)]n = [2(  2 + 1)]n + [2(
2 + 1)]n + [2(  3 + 1)]n ,
3 + 1)]n ,
где для определённости возьмём  1 >
1 >  2 >
2 >  3
3
После упрощения.
(  1 + 1)n = (
1 + 1)n = (  2 + 1)n + (
2 + 1)n + (  3 + 1)n
3 + 1)n
По сути, природа этого уравнения та же, что и уравнения ВТФ, т.к. зависимость между Х, У, Z и столбцами матрицы  i – функции соответствующие линейным уравнениям.
i – функции соответствующие линейным уравнениям.
Можно составить систему подобных уравнений.



………………………………………… (а)


Каждое уравнение этой системы также является функциональным уравнением ВТФ.
Для обоснования данного утверждения рассмотрим следующий пример.
Вычислим несколько значений  соответствующих числу 10 по формуле чётных чисел.
соответствующих числу 10 по формуле чётных чисел.
2(  1 + 1)=10
1 + 1)=10  1 =4
1 =4
2(  2 + 2)=10
2 + 2)=10  2 =3
2 =3
2(  3 + 3)=10
3 + 3)=10  3 =2
3 =2
Т.е. переменная  может принимать значения от 1 до ¥.
может принимать значения от 1 до ¥.
Условием для существования системы уравнений (а) служат лишь условия
 и
и  .
.
Данные условия слабее условий существования пифагоровых троек, где, если (а, в, с) – пифагорова тройка, то таковою будет и тройка (nа, nв, nс), при всех n = 1, 2, 3 …
Т.е. система (а) должна быть справедливой для всего ряда натуральных чисел, при условии неизменности величин р и f, и условии  3 +1<½K½<¥.
3 +1<½K½<¥.
Это следует при предположении справедливости уравнения ВТФ –  .
.
У системы уравнений (а) есть 2 варианта:
- I - каждое уравнение системы имеет решение;
- II - каждое из уравнений системы не имеет решений.
Если взять в уравнении системы к = -  3, тогда уравнение примет вид
3, тогда уравнение примет вид

Данное уравнение вида 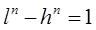 не может иметь решений в целых числах при n>2.
не может иметь решений в целых числах при n>2.
Тогда не верно любое уравнение системы и следовательно не верно и уравнение ВТФ.
Рассматривались чётные значения Х, У, Z.
В системе уравнений (а) переменные  I принимают значения всех чисел натурального ряда, и чётных и не чётных. Тогда ВТФ тоже доказана для всего ряда натуральных чисел. Если же рассматривать варианты II и III доказательства ВТФ, тогда функциональные уравнения примут вид:
I принимают значения всех чисел натурального ряда, и чётных и не чётных. Тогда ВТФ тоже доказана для всего ряда натуральных чисел. Если же рассматривать варианты II и III доказательства ВТФ, тогда функциональные уравнения примут вид:
II [2(  1+1)]n=[2(
1+1)]n=[2(  2+1)-1]n+[2(
2+1)-1]n+[2(  3+1)-1]n
3+1)-1]n
III [2(  1+1)-1]n=[2(
1+1)-1]n=[2(  2+1)]n+[2(
2+1)]n+[2(  3+1)-1]n
3+1)-1]n
Принципиально в доказательстве ВТФ это ничего не меняет.
Для обоснования данного, довольно – таки экзотического на сегодняшний день метода, далее будут рассмотрены некоторые известные задачи.
Уравнение Пелля
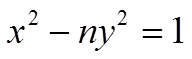 (1)
(1)
Рассмотрим 3 варианта:
- I Х - чётное число, У - нечётное число, n - нечётное число;
- II Х - нечётное число, У - нечётное число, n - чётное число;
- III Х - нечётное число, У - чётное число, n – любое, и чётное, и нечётное число.
И всегда ½Х½ > ½У½
Вариант I.
Составим функциональное уравнение.
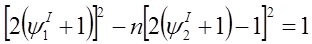 , где, конечно же,
, где, конечно же,  1 >
1 >  2
2
Возьмём к = -  2, тогда
2, тогда

После преобразований
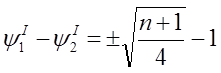 (2)
(2)
где  ;
;  .
.
Окончательно, после подстановки будет
 , где n = 3, 15 . . . . .
, где n = 3, 15 . . . . .
Проверим при n = 3
а) 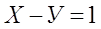 ,
, 
б)  ,
, 
Подставим (а) в уравнение (1)



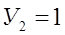

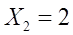
Для случая Х = 2, У = 1, n = 3 будет

Подставим (б) в уравнение (1)




Для 

Проверка даёт

Для 

Проверка даёт

Составим последующее функциональное уравнение.

После упрощения

где  ,
, 
После подстановки

Следующее функциональное уравнение примет вид
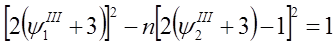
После упрощения

где  ,
, 
После подстановки

Получилась система бесконечных решений:



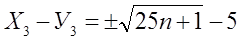 (3)
(3)
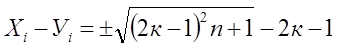
Вариант II.
Функциональное уравнение примет вид.


|
из
5.00
|
Обсуждение в статье: Великая теорема Ферма. Решение |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы


