 |
Главная |
Непр. элементарн.ф-ций.
|
из
5.00
|
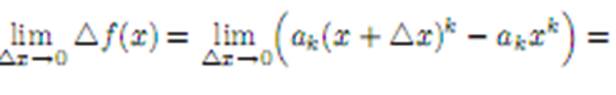 Постоянная функция.Функция f(x) = C, где C = const, ∀x ∈ X непрерывна в любой точке x0, поскольку
Постоянная функция.Функция f(x) = C, где C = const, ∀x ∈ X непрерывна в любой точке x0, поскольку 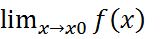 =
= 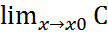 =С=f(x0). Многочлены и рациональные функции.ФункцияPn(x) = a0xn + a1xn−1+ . . . + an−1x + an,где ai, i = 0, n – действительные числа, называется многочленом от x степени n.Докажем сначала непрерывность функции f(x) = akxk в любой точке x ∈ R. Согласно биному Ньютона
=С=f(x0). Многочлены и рациональные функции.ФункцияPn(x) = a0xn + a1xn−1+ . . . + an−1x + an,где ai, i = 0, n – действительные числа, называется многочленом от x степени n.Докажем сначала непрерывность функции f(x) = akxk в любой точке x ∈ R. Согласно биному Ньютона

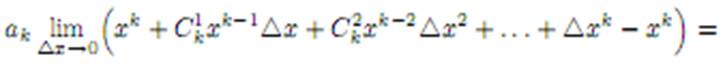
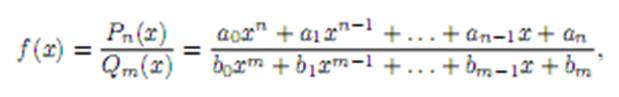 Отсюда заключаем, что функция f(x) = akxk непрерывна в любой точке x∈R. Тогда многочлен Pn(x) является непрерывной функцией в любой точке x∈R как сумма непрерывных функций вида akxk, k = 0, n. Рациональной называется функция вида
Отсюда заключаем, что функция f(x) = akxk непрерывна в любой точке x∈R. Тогда многочлен Pn(x) является непрерывной функцией в любой точке x∈R как сумма непрерывных функций вида akxk, k = 0, n. Рациональной называется функция вида
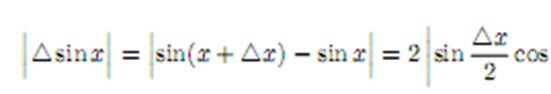 где Pn(x), Qm(x) – многочлены степеней n и m cоответственно. Рациональная функция во всех точках, в которых Qm(x) не обращается в нуль, непрерывна как отношение двухнепрерывных функций.Тригонометрические функции:Докажем непрерывность функции f(x) = sin x в любой точке x ∈ R. Имеем
где Pn(x), Qm(x) – многочлены степеней n и m cоответственно. Рациональная функция во всех точках, в которых Qm(x) не обращается в нуль, непрерывна как отношение двухнепрерывных функций.Тригонометрические функции:Докажем непрерывность функции f(x) = sin x в любой точке x ∈ R. Имеем
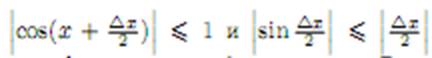
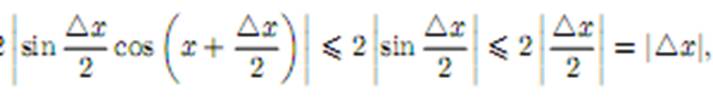
так как Отсюда следует, что если | 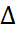 x| < δ = ε, то и |
x| < δ = ε, то и | 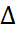 sin x| < ε, т.е. sin xнепрерывная функция в любой точке x ∈ R.Аналогично доказывается непрерывность функции cos x в любой точке x ∈ R.Функция tg x =
sin x| < ε, т.е. sin xнепрерывная функция в любой точке x ∈ R.Аналогично доказывается непрерывность функции cos x в любой точке x ∈ R.Функция tg x =  непрерывна в точках, где x
непрерывна в точках, где x 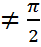 + πn, n ∈ Z. Функция ctg x =
+ πn, n ∈ Z. Функция ctg x = 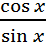 непрерывна, если x
непрерывна, если x 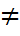 πn,n ∈ Z.
πn,n ∈ Z.
Степенная функция f(x) = xa. Непрерывность этой функции при x> 0 вытекает из непрерывности сложной функции и представления xa = ealnx. Если же функция xa имеет смысл и для x < 0 (например, x4,3√x), то при a > 0 она будет непрерывной для ∀x ∈ R, апри a < 0 – для всех x ∈ R кроме x 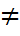 0.
0.
30 Дифференцируемость функций. Дифференциал и произв.
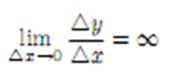
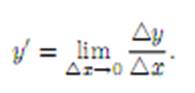 Определение 1. Пусть функция y = f(x) определена в некоторой окрестности точки x0 ∈ R и пусть x–произвольнаяточка этой окрестности. Если отношение
Определение 1. Пусть функция y = f(x) определена в некоторой окрестности точки x0 ∈ R и пусть x–произвольнаяточка этой окрестности. Если отношение  имеет gредел при x → x0, то этот предел называется производной функции f(x) в точке x0, и обозначается f ’(x0):
имеет gредел при x → x0, то этот предел называется производной функции f(x) в точке x0, и обозначается f ’(x0): 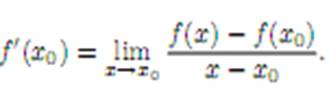 Если ввести обозначения x−x0 =
Если ввести обозначения x−x0 = 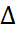 x, f(x0+
x, f(x0+ 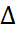 x)−f(x0) =
x)−f(x0) = 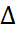 y, то получаем еще одну запись определения производной: Если для
y, то получаем еще одну запись определения производной: Если для
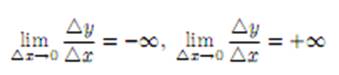 некоторого значения x0 существуют пределы или то говорят, что при x = x0
некоторого значения x0 существуют пределы или то говорят, что при x = x0
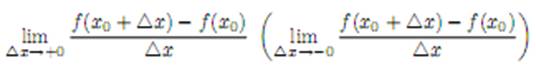 существует бесконечная производная или соответственно бесконечная производная определенного знака, равная −
существует бесконечная производная или соответственно бесконечная производная определенного знака, равная − 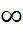 или +
или + 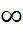 .В дальнейшем под выражением «функция имеет производную» будем понимать всегда наличие конечной производной, если не оговорено противное. Определение 2. Если функция f(x) определена в некоторой правосторонней (левосторонней) окрестности точки x0 исуществует конечный или бесконечный (определенного знака) предел
.В дальнейшем под выражением «функция имеет производную» будем понимать всегда наличие конечной производной, если не оговорено противное. Определение 2. Если функция f(x) определена в некоторой правосторонней (левосторонней) окрестности точки x0 исуществует конечный или бесконечный (определенного знака) предел
то он называется соответственно конечной или бесконечной правой (левой) производной функции f(x) в точке x0 иобозначается f ’+(x0) (f ’−(x0)) Правая и левая производные называются односторонними производными. Из теоремы об односторонних пределах следует, что функция f(x), определенная в некоторой окрестности точки x0, имеет производную f ’(x0) тогда и только тогда, когда f ’+(x0) и f ‘−(x0) существуют и f’+(x0) = f’−(x0). В этом случае f’(x0) = f’+(x0) = f’−(x0).Если функция f(x) определена на некотором промежутке и в каждой его точке существует производная (причем под производной в конце этого промежутка, который принадлежит промежутку, понимается соответствующая односторонняя производная), то она также является функцией, определенной на данном промежутке, ее обозначают f’(x). Теорема 1. Для того чтобы функция f(x) была дифференцируемой в некоторой точке x0, необходимо и достаточно,чтобы она имела в этой точке производную, при этом dy = f’(x0) dx.Доказательство. Пусть функция f(x) дифференцируема в точке x0, т.е 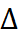 y = A·
y = A· 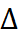 x+o(
x+o( 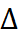 x),
x), 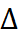 x → 0.Тогда
x → 0.Тогда  = A +
= A + 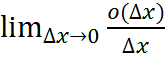 = A. Поэтому производная f’(x0) существует и равна A. Отсюда dy= f’(x0) dx. Теорема 2. Если функция f(x) дифференцируема в некоторой точке, то она и непрерывна в этой точке. Следствие 1. Если функция в некоторой точке имеет производную, то она и непрерывна в этой точке. Обратим внимание на то, если функция в точке имеет бесконечную производную, то она может быть разрывной в этой точке. Заметим, что утверждение, обратное теореме 2, неверно, т.е. из непрерывности функции f(x) в данной точке не следует ее дифференцируемость.
= A. Поэтому производная f’(x0) существует и равна A. Отсюда dy= f’(x0) dx. Теорема 2. Если функция f(x) дифференцируема в некоторой точке, то она и непрерывна в этой точке. Следствие 1. Если функция в некоторой точке имеет производную, то она и непрерывна в этой точке. Обратим внимание на то, если функция в точке имеет бесконечную производную, то она может быть разрывной в этой точке. Заметим, что утверждение, обратное теореме 2, неверно, т.е. из непрерывности функции f(x) в данной точке не следует ее дифференцируемость.
|
из
5.00
|
Обсуждение в статье: Непр. элементарн.ф-ций. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

