 |
Главная |
Непрерывность ф-ции, имеющей производную.
|
из
5.00
|
Теорема 2. Если функция f(x) дифференцируема в некоторой точке, то она и непрерывна в этой точке. Доказательство. Пусть функция f(x) дифференцируема в точке x0, т.е  y = A ·
y = A ·  x + o(
x + o(  x),
x),  x → 0.
x → 0.  = A
= A  +
+  = 0, что и означает непрерывность функции f(x) в точке x0.
= 0, что и означает непрерывность функции f(x) в точке x0.
Следствие 1. Если функция в некоторой точке имеет производную, то она и непрерывна в этой точке. Обратим внимание на то, если функция в точке имеет бесконечную производную, то она может быть разрывной в этой точке. Заметим, что утверждение, обратное теореме 2, неверно, т.е. из непрерывности функции f(x) в данной точке не следует ее дифференцируемость.
32.Геометр.смысл. произв. Физ. Смысл. Произв. Рассмотрим задачу о проведении касательной к произвольной плоской кривой. Пусть L – дуга плоской кривой, M0 –точка этой кривой, M0M – секущая. Если точка M движется по кривой к точке M0,то секущая поворачивается вокруг точки M0 и стремится к некоторому предельному положению M0T. Определение 4. Касательной к кривой L в точке M0 называется прямая M0T, которая представляет собой предельное положение секущей M0M при стремлении по кривой точки M к точке M0.Если предельного положения секущей не существует, то говорят, что в точке M0 провести касательную нельзя. Это бывает в случае, когда точка M0 является точкой излома или заострения кривой. Пусть кривая L является графиком функции f(x) и точка M0(x0, f(x0)) ∈ L. Предположим, что касательная к кривой в точке M0 существует. Угловой коэффициент секущей M0M k = tg  =
=  . Если
. Если 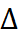 x → 0, то точка M движется по кривой к точке M0 и секущая M0M стремится к своему предельному положению M0T. Таким образом, k = tgα =
x → 0, то точка M движется по кривой к точке M0 и секущая M0M стремится к своему предельному положению M0T. Таким образом, k = tgα =  =
=  =f ’(x0). (1) т.е. если кривая L является графиком функции f(x), то из равенства (1) следует геометрический смысл производной: производная от функции f(x) при x = x0 равна угловому коэффициенту касательной к графику функции в точке с абсциссой x . Тогда уравнение касательной y − f(x0) = f’(x0)(x − x0)или y − y0 = f ’(x0)(x − x0) (2).Заметим, что в правой части уравнения (2) стоит дифференциал, поэтому геометрический смысл дифференциала состоит в следующем: дифференциал - это приращение ординаты касательной.физика: Рассмотрим функцию y = f(x), определенную и непрерывную в некоторой окрестности точки x0. Если аргумент x0 функции получает приращение
=f ’(x0). (1) т.е. если кривая L является графиком функции f(x), то из равенства (1) следует геометрический смысл производной: производная от функции f(x) при x = x0 равна угловому коэффициенту касательной к графику функции в точке с абсциссой x . Тогда уравнение касательной y − f(x0) = f’(x0)(x − x0)или y − y0 = f ’(x0)(x − x0) (2).Заметим, что в правой части уравнения (2) стоит дифференциал, поэтому геометрический смысл дифференциала состоит в следующем: дифференциал - это приращение ординаты касательной.физика: Рассмотрим функцию y = f(x), определенную и непрерывную в некоторой окрестности точки x0. Если аргумент x0 функции получает приращение 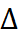 x (положительное или отрицательное), такое, что x0+
x (положительное или отрицательное), такое, что x0+ 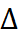 x принадлежит той же окрестности точки x0, то соответствующее приращение функции
x принадлежит той же окрестности точки x0, то соответствующее приращение функции 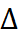 f(x0) = f(x0 +
f(x0) = f(x0 + 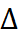 x) − f(x0), средняя скорость изменения функции vср =
x) − f(x0), средняя скорость изменения функции vср =  , а мгновенная скорость ее изменения v =
, а мгновенная скорость ее изменения v =  =f ’(x0) В этом состоит механический смысл производной, т.е. производная -математическая модель мгновенной скорости процесса, описываемого функцией f(x). В зависимости от содержательной сущности функции можно получить широкий круг математических моделей скорости протекания процессов. Рассмотрим некоторые из них. 1. Пусть материальная точка M движется неравномерно и y = s(t) – функция, устанавливающая зависимость пути от времени t. Тогда мгновенная скорость движения в момент времени t0 есть производная от пути s по времени t: v =
=f ’(x0) В этом состоит механический смысл производной, т.е. производная -математическая модель мгновенной скорости процесса, описываемого функцией f(x). В зависимости от содержательной сущности функции можно получить широкий круг математических моделей скорости протекания процессов. Рассмотрим некоторые из них. 1. Пусть материальная точка M движется неравномерно и y = s(t) – функция, устанавливающая зависимость пути от времени t. Тогда мгновенная скорость движения в момент времени t0 есть производная от пути s по времени t: v =  |t=t0 =
|t=t0 =  =
= 
33. Правила вычисления производных. Теорема 3. Если функции f : X → R, g : X → R дифференцируемы в точке x ∈ X, то а) их сумма дифференцируема в x, причем (f + g)’(x) = (f’+ g’)(x); б) их произведение дифференцируемо в x, причем (f · g)’(x) = f’(x)g(x) + f(x)g’(x); в) их отношение дифференцируемо в x, если g(x)  0, причем(
0, причем(  ) ‘(x) =
) ‘(x) = 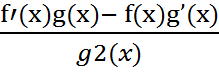
Следствие 1. Производная от линейной комбинации дифференцируемых функций равна линейной комбинации производных этих функций. Следствие 2. Если функции f1(x), f2(x), . . . , fn(x) дифференцируемы в точке x, то. (f1 · f2 · . . . · fn)’(x) = f’1(x) · f2(x) · . . . · fn(x) + f1(x) · f’2(x) · . . . · fn(x) + . . . + f1(x) · f2(x) · . . . · f’n(x).
Следствие 3.Из взаимосвязи производной и дифференциала следует, что теорема 3 может быть записана также через дифференциалы, т.е. а) d(f + g)(x) = df(x) + dg(x), в) d(f · g)(x) = g(x) · df(x) + f(x) · dg(x); с) d(  ) (x) =
) (x) = 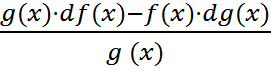 , если g(x)
, если g(x)  = 0.
= 0.
|
из
5.00
|
Обсуждение в статье: Непрерывность ф-ции, имеющей производную. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

