 |
Главная |
Дифференцирование композиции функций.
|
из
5.00
|
Теорема 4. Если функция f :X → Y⊂Rдифференцируемавточкеx, афункцияg :Y→Rдифференцируемав
точке y = f(x) ∈Y , токомпозицияg◦f :X→Rэтихфункций дифференцируема в точке x, причем
(g ◦ f)’(x) = g’(f) · f’(x).
35 Дифференцирование обратной функции.
Теорема 5 (О производной обратной функции). Пусть функции f: X→Y, f-1: Y→X взаимно обратны и непрерывны в точках x0∈X и f(x0) = y0∈Y соответственно. Если функция f(x) дифференцируема в точке x0 и f≠0, то функция f-1 также дифференцируема в точке y0 , причем (f-1)’(y0)=1/f’(x0).
Доказательство. Из непрерывности f(x) в x0 и f-1в y0 можно заключить, что при x→x0 , x∈X имеем y = f(x) → y0, y=f(x) ∈ Y и y=f(x)≠ y0 , если x≠x0 . Используя теперь теорему о пределе композиции функций и арифметические свойства предела, находим 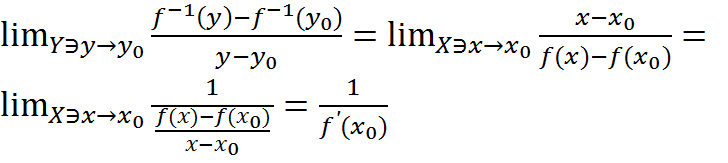 .
.
Таким образом, показано, что в точке y0 функция f−1 : Y→X имеет производную и (f-1)’(y0)=1/f’(x0).
Замечание 1. Если бы заранее было известно, что функция f−1 дифференцируема в точке y0, то из тождества (f−1○f)(x) ≡ x по теореме о дифференцировании композиции функции сразу бы нашли, что (f−1)’ (y0 )·f’(x0) = 1.
Замечание 2. Теореме можно дать геометрическую интерпретацию. Как известно, 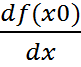 =tgα, где α – значение угла, образуемого касательной графика функции f(x) в точке (x0, y0 ) с положительным направлением оси Ox, тогда
=tgα, где α – значение угла, образуемого касательной графика функции f(x) в точке (x0, y0 ) с положительным направлением оси Ox, тогда
 , где β – значение угла, образованного той же касательной с осью Oy. Действительно, поскольку β =
, где β – значение угла, образованного той же касательной с осью Oy. Действительно, поскольку β =  −α, то
−α, то 
36 Производные элементарных функций.
а). Производная и дифференциал логарифмической функции. Пусть y = log a x, где a > 0,a  1. Тогда
1. Тогда  y = log a (x +
y = log a (x +  x) – log a x = log a(1 +
x) – log a x = log a(1 +  ). Следовательно, по определению y0=
). Следовательно, по определению y0=  =
=  =
=  loga
loga 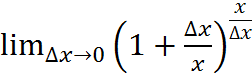 =
=  logae=
logae=  . Здесь воспользовались вторым замечательным пределом и непрерывностью логарифмической функции. Итак, y = logax⇒y0=
. Здесь воспользовались вторым замечательным пределом и непрерывностью логарифмической функции. Итак, y = logax⇒y0=  logae=
logae=  ⇒dy =
⇒dy =  . б). Производная и дифференциал степенной функции Пусть y =(u(x))α, α∈R. Рассмотрим вначале случай, когда u(x) > 0. Если u(x) > 0, то lny = αlnu(x). Продифференцируем полученное равенство почленно по правилу дифференцирования сложной функции, считая y функцией от x: (lny)’ = (αlnu(x))’ ⇒
. б). Производная и дифференциал степенной функции Пусть y =(u(x))α, α∈R. Рассмотрим вначале случай, когда u(x) > 0. Если u(x) > 0, то lny = αlnu(x). Продифференцируем полученное равенство почленно по правилу дифференцирования сложной функции, считая y функцией от x: (lny)’ = (αlnu(x))’ ⇒ 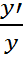 =
=  ⇒ dy =
⇒ dy =  . Пусть теперь u(x) < 0. Представим функцию y = (u(x))α в виде (−1)α (v(x))α , где v(x) > 0. Тогда y’= (−1)αα(v(x))α−1v’(x) = α(u(x))α−1u’(x). Итак y =(u(x))α
. Пусть теперь u(x) < 0. Представим функцию y = (u(x))α в виде (−1)α (v(x))α , где v(x) > 0. Тогда y’= (−1)αα(v(x))α−1v’(x) = α(u(x))α−1u’(x). Итак y =(u(x))α
⇒ y’= α(u(x))α−1u’(x) ⇒ dy = α(u(x))α−1du(x).
37. Производные и дифференциалы высших порядков 1. Производные высших порядков.
Пусть f : X → Y функция, дифференцируемая в каждойточке x∈X. Ее производная в точке x есть некоторая функция g(x) = f’(x). Если функция g(x) дифференцируема, то имеет смысл определить ее производную g’(x) =(f’(x))’, которая называется второй производной функции f(x) и обозначается f’’(x). Таким образом, f’’(x) =(f’(x))’. Аналогично f’’(x) может оказаться дифференцируемой функцией в точке x, тогда f’’’(x)=(f’’(x))’ есть третья производная функции f(x). Точно так же, если в точке x определена производная порядка n−1 функции f(x), то производная порядка n или n-ая производная функции f(x) определяется формулой f(n)(x)=(f(n-1)(x))’ , n=1,2,…
Отметим, что в формуле принято f(0)(x) = f(x), т.е. производная нулевого порядка есть сама функция.
Для n-ой производной функции f(x) применяются и другие обозначения: f(n)xx…x(x), f(n)xn(x),  .
.
Функция f(x) называется n раз дифференцируемой в точке x∈X, если в этой точке у нее существуют все производные до n-го порядка включительно.
Если f(x) дифференцируема n раз в каждой точке x∈X и f(n)(x) является непрерывной функцией на X, то f(x) называется n раз непрерывно дифференцируемой функцией или функцией класса C(n)[X]. Множество непрерывных функций, определенных на X, обозначается C[X]. Функция, имеющая производную любого порядка, называется бесконечно дифференцируемой.
2.Дифференциалы высших порядков.
Пусть функция f : X → Y дифференцируема и df = f’(x)dx - ее дифференциал. Дифференциалом второго порядка называется дифференциал от дифференциала первого порядка, который обозначается d2f, то есть d2f = d(df). Дифференциал n-го порядка есть dnf = d(dn-1f).
Если x – независимая переменная, а dx – постоянная (не зависит от x) и функция f имеет n производных, то, учитывая, что (dx)’=(dx)’’=…=(dx)(n)=0 последовательно находим: df=f’(x)dx, d2f=d(f’(x)dx)=(f’(x)dx)’dx=f’’(x)(dx)2=f’’(x)dx2, … , dnf=d(f(n-1)(x)dxn-1)=f(n)(x)dxn.
Предположим теперь, что x есть некоторая функция параметра t, то есть x = ϕ(t), t∈T. Тогда f является сложной функцией f(ϕ (t)) и ее первый дифференциал, как известно, обладает свойством инвариантности формы. Покажем, что дифференциалы более высокого порядка в этом случае инвариантностью не обладают.
В самом деле, если x - независимая переменная, то d2f=f’’xxdx2.
Если же f = f(x), x = ϕ(t), то d2f=d(df)=d(f’xdx)=df’x.dx+f’x.d(dx)=f’’xxdx2+f’xd2x,
что не совпадает с полученной выше формулой для d2f в случае независимой переменной.
Теорема Ферма.
Определение 1. Точка x0∈ X называется точкой локального максимума (минимума) функции f(x), а значение в ней локальным максимумом (минимумом), если существует окрестность V (x0 ) точки x0 , такая, что ∀x ∈ V (x0 ) имеем f(x)≤f(x0) (f(x)≥f(x0)).
Определение 2. Точка x0∈X называется точкой строгого локального максимума (минимума) функции f(x), если существует проколотая окрестность  (x0) точки x0, такая, что ∀x∈
(x0) точки x0, такая, что ∀x∈  (x0) имеем f(x) <f(x0) (f(x)>f(x0)).
(x0) имеем f(x) <f(x0) (f(x)>f(x0)).
Определение 3. Точки локального максимума и минимума называются точками локального экстремума, а значения функции в них - локальными экстремумами функции.
Заметим, что если x0 точка строгого локального экстремума функции f(x), то приращение ∆f(x0 ) = f(x0 + ∆x) − f(x0), ∀x ∈  (x0) сохраняет знак.
(x0) сохраняет знак.
Теорема 6 (Ферма). Пусть функция f(x) определена на интервале (a;b) и в некоторой точке x0∈ (a; b) имеет локальный экстремум. Тогда, если в точке x0 существует конечная производная f’(x0), то f’(x0) = 0.
Доказательство. Пусть для определенности в точке x0 функция имеет локальный минимум, т.е. f(x)≥f(x0),∀x ∈ V (x0). Тогда в силу дифференцируемости функции f(x) в точке x0 при x > x0 получим 
а при x < x0 будем иметь 
Эти неравенства имеют место одновременно лишь при f’+(x0)=f’-(x0)=f’(x0)=0.
Замечание 1. Геометрический смысл теоремы Ферма состоит в следующем: если точка x0 ∈ (a; b) является точкой максимума или минимума функции и существует f’(x0), то касательная, проведенная к графику функции в точке (x0,f(x0))параллельна оси Ox.
Замечание 2. Оба условия – интервал (a;b) и дифференцируемость функции в точке локального экстремума – обяза- тельны для справедливости теоремы Ферма. Действительно, пусть f(x) = |x|, x∈ (−1;1). В точке x0= 0 функция f(x) имеет локальный минимум, но в ней она не дифференцируема. В данном случае условие существования производной в точке локального минимума нарушено и поэтому теорема Ферма не имеет места.
Пусть теперь f(x) = x3, x∈ [−1;1]. В точке x0 = 1 имеется краевой максимум, но f’(1)=3≠0. Теорема Ферма не применима в данном случае, поскольку x = 1  (−1;1).
(−1;1).
39 Теорема Ролля.
Теорема 7. Пусть функция f(x) непрерывна на отрезке [a;b], дифференцируема в каждой точке интервала (a; b) и f(a) = f(b). Тогда существует хотя бы одна точка ξ, a<ξ<b, такая, что f’(ξ) = 0.
Доказательство. Если f(x) – постоянная на [a; b], то f’(x) = 0, ∀x ∈ (a; b).
Пусть теперь f(x) не является постоянной функцией. Непрерывная на отрезке [a;b] функция по теореме Вейерштрасса достигает в некоторых точках отрезка [a; b] наибольшего и наименьшего значений. Поскольку f(x) не является постоянной, то или  или
или  обязательно достигаются функцией во внутренней точке ξ отрезка [a; b].
обязательно достигаются функцией во внутренней точке ξ отрезка [a; b].
По теореме Ферма f’(ξ) = 0.
Замечание 3. Геометрический смысл теоремы Ролля следующий: при выполнении условий теоремы внутри отрезка [a;b] обязательно найдется хотя бы одна точка ξ, такая, что касательная к графику f(x) в точке (ξ,f(ξ)) параллельна оси Ox.
Следствие 1 (Обобщенная теорема Ролля). Пусть функция f(x) n раз непрерывно дифференцируема на отрезке [a; b] и обращается в нуль в n + 1-й точке x0 , x1 , x2 , ... ,xn этого отрезка. Тогда существует такое число ξ∈ (a;b), что f(n)(ξ) = 0.
Доказательство. Для простотырассуждений ограничимся случаем n = 2, т.е. функция f(x) обращаетсяв нуль в точках x0 , x1 , x2 . Для определенности будем считать, что x0<x1<x2 . Так как f(x0) = f(x1) = f(x2) = 0, то по теореме Ролля существует ξ1 ∈ (x0; x1), что f’(ξ1) = 0, и существует, ξ2∈(x1;x2), что f’(ξ2)=0. Итак, на концах отрезка [ξ1;ξ2] выполнено условие f’(ξ1 )=f’(ξ2) = 0. По теореме Ролля на отрезке [ξ1 ;ξ2] существует точка ξ в которой f’’(ξ) = 0.
Теорема Лагранжа
Теорема 8. Если функция f(x) непрерывна на отрезке [a; b] и дифференцируема на интервале (a; b), то существует по крайней мере одна точка ξ ∈ (a; b), такая, что f(b) − f(a) = f’(ξ)(b − a). Доказательство. Составим вспомогательную функцию  (x) = (b − a)f(x) –(f(b) −f(a))x. Покажем, что функция
(x) = (b − a)f(x) –(f(b) −f(a))x. Покажем, что функция  (x) удовлетворяет условиям теоремы Ролля. Действительно: 1)
(x) удовлетворяет условиям теоремы Ролля. Действительно: 1)  (x) непрерывна на [a; b], так как является суммой непрерывных на [a; b] функций; 2)
(x) непрерывна на [a; b], так как является суммой непрерывных на [a; b] функций; 2)  (x) дифференцируема на (a; b), так как является суммой дифференцируемых на (a; b) функций; 3)
(x) дифференцируема на (a; b), так как является суммой дифференцируемых на (a; b) функций; 3)  (a) =
(a) =  (b) = bf(a) − af(b). Итак,
(b) = bf(a) − af(b). Итак,  (x) удовлетворяет условиям теоремы Ролля, причем
(x) удовлетворяет условиям теоремы Ролля, причем  ‘(x) = (b − a)f ‘(x) – (f(b) − f(a) ). По теореме Ролля существует точка ξ ∈ (a; b), такая, что
‘(x) = (b − a)f ‘(x) – (f(b) − f(a) ). По теореме Ролля существует точка ξ ∈ (a; b), такая, что  ‘(ξ) = 0, т.е. (b − a)f’(ξ) –(f(b) − f(a))= 0 ⇔ f(b) − f(a) = f’(ξ)(b − a).
‘(ξ) = 0, т.е. (b − a)f’(ξ) –(f(b) − f(a))= 0 ⇔ f(b) − f(a) = f’(ξ)(b − a).
41 Теорема Коши.Обобщением теоремы Лагранжа является теорема Коши.
 Теорема 9. Пусть функции f(x) и g(x) удовлетворяют следующим условиям: 1) непрерывны на отрезке [a; b]; 2) дифференцируемы в интервале (a; b), причем g‘(x)
Теорема 9. Пусть функции f(x) и g(x) удовлетворяют следующим условиям: 1) непрерывны на отрезке [a; b]; 2) дифференцируемы в интервале (a; b), причем g‘(x)  0, ∀x ∈ (a; b). Тогда существует по крайней мере одна точка ξ ∈ (a; b) такая, что
0, ∀x ∈ (a; b). Тогда существует по крайней мере одна точка ξ ∈ (a; b) такая, что
Доказательство. Составим вспомогательную функцию 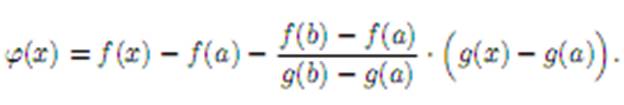
Заметим, что g(b)  g(a). Действительно, если бы g(b) = g(a), то для функции g(x) на отрезке [a; b] были бы выполнены все условия теоремы Ролля, и по этой теореме внутри отрезка [a; b] нашлась бы по крайней мере одна точка ξ, для которой g’(ξ) = 0, что противоречит условию теоремы. Следовательно g(b)
g(a). Действительно, если бы g(b) = g(a), то для функции g(x) на отрезке [a; b] были бы выполнены все условия теоремы Ролля, и по этой теореме внутри отрезка [a; b] нашлась бы по крайней мере одна точка ξ, для которой g’(ξ) = 0, что противоречит условию теоремы. Следовательно g(b)  g(a).
g(a).
Покажем, что вспомогательная функция  (x) удовлетворяет условиям теоремы Ролля. действительно: 1)
(x) удовлетворяет условиям теоремы Ролля. действительно: 1)  (x) непрерывна на [a; b] как сумма непрерывных на [a; b] функций; 2)
(x) непрерывна на [a; b] как сумма непрерывных на [a; b] функций; 2)  (x) дифференцируема на интервале (a; b) как сумма дифференцируемых на (a; b) функций; 3)
(x) дифференцируема на интервале (a; b) как сумма дифференцируемых на (a; b) функций; 3)  (a) = 0,
(a) = 0,  (b) = 0 поэтому и
(b) = 0 поэтому и  (a) =
(a) =  (b). Найдем
(b). Найдем

По теореме Ролля существует точка ξ ∈ (a; b) такая, что  (ξ) = 0, поэтому
(ξ) = 0, поэтому 

42-43 Раскрытие неопределенностей. Остановимся на одном частном, но полезном приеме отыскания предела отношения функций, известном как правило Лопиталя.
Теорема 10 (Неопределенность вида 0/0 ).Пусть:
 1) функции f(x) и g(x) определены в промежутке (a; b];
1) функции f(x) и g(x) определены в промежутке (a; b];
3) в промежутке (a; b] существуют конечные производные f’(x) и g’(x), причем g’(x)  0; 4) существует (конечный или бесконечный) предел
0; 4) существует (конечный или бесконечный) предел  Доказательство. Дополним определения функций f(x) и g(x), положив их при x = a равными нулю: f(a) = g(a) = 0. Тогда эти функции окажутся непрерывными во всем замкнутом промежутке [a; b]; их значения в точке a совпадают с пределами при x → a, а в прочих точках непрерывность вытекает из существования конечных производных. Применяя теорему Коши, получим
Доказательство. Дополним определения функций f(x) и g(x), положив их при x = a равными нулю: f(a) = g(a) = 0. Тогда эти функции окажутся непрерывными во всем замкнутом промежутке [a; b]; их значения в точке a совпадают с пределами при x → a, а в прочих точках непрерывность вытекает из существования конечных производных. Применяя теорему Коши, получим
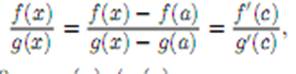
где a < c < x. То обстоятельство, что g(x)  0, т.е. g(x)
0, т.е. g(x)  g(a) есть следствие предложения g’(x) = 0. Когда x → a, очевидно, и c → a, так что, в силу условия 4)
g(a) есть следствие предложения g’(x) = 0. Когда x → a, очевидно, и c → a, так что, в силу условия 4) 
Теорема 11 (Неопределенность вида ∞/∞). Пусть: 1) функции f(x) и g(x) определены в промежутке (a; b]; 
3) существуют в промежутке (a; b] конечные производные f’(x) и g’(x), причем g’(x)  0;
0;
4) существует (конечный или бесконечный) предел 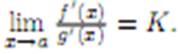
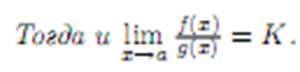
|
из
5.00
|
Обсуждение в статье: Дифференцирование композиции функций. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

