 |
Главная |
Понятие линейной зависимости (независимости) векторов. Свойства ЛЗ, ЛНЗ.
|
из
5.00
|
Определение.
Выражение вида 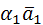 +
+  2
2  +…+
+…+  называется линейной комбинацией векторов
называется линейной комбинацией векторов  …
…  .
.
Линейная комбинация – тривиальная, если все её коэффициенты = 0.
- нетривиальная, когда хотя бы один коэффициент отличен от 0.
Если вектор  может быть представлен в виде
может быть представлен в виде  =
= 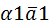 +…+
+…+  , то говорят, что
, то говорят, что  линейно выражается через
линейно выражается через  …
…  .
.

|

|
1.

|
|

|

|
 выражен через
выражен через 
 .
.

|

|
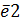
|

|
 =3
=3  + 2
+ 2 
Система векторов  …
…  называется линейно зависимой (ЛЗ), если существует нетривиальная линейная комбинация этих векторов, равная нулю.
называется линейно зависимой (ЛЗ), если существует нетривиальная линейная комбинация этих векторов, равная нулю.
 ,
,  ,
,  (прим.2.)
(прим.2.)
Замечание. Иными словами, если хотя бы один вектор из системы выражается через остальные, то система будет ЛЗ.
Система векторов  …
…  называется линейно независимой (ЛНЗ), если только тривиальная линейная комбинация этих векторов равна нулю.
называется линейно независимой (ЛНЗ), если только тривиальная линейная комбинация этих векторов равна нулю.
Рассмотрим  ,
,  (прим.2.)
(прим.2.)
 *
*  +
+  *
*  =
=  , только если
, только если  =
=  =0
=0
Замечание. Иными словами, система векторов – ЛНЗ, если ни один из векторов не выражается через остальные.
Свойства линейной зависимости.
1) Если система векторов содержит  , то она – ЛЗ.
, то она – ЛЗ.
 ,
,  , … ,
, … , 
2) Всякая подсистема линейно независимой системы линейных векторов сама является ЛНЗ.
 …
…  - ЛНЗ
- ЛНЗ
Предположим  , … ,
, … ,  – ЛЗ Þ
– ЛЗ Þ  *
*  + … +
+ … + 
 =
= 
 i
i  0
0
 *
*  + … +
+ … + 
 +
+  *
*  + … +
+ … + 
 =
=  Þ
Þ  i
i  0
0
Исходная система ЛЗ, значит предположение неверно.
3) Если система векторов содержит два пропорциональных вектора, то она линейно зависима.
 ,
, 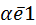 ,
,  …
… 
4) Если система векторов  …
…  - ЛНЗ и
- ЛНЗ и  –линейно выражается через эти векторы, то такое выражение единственно.
–линейно выражается через эти векторы, то такое выражение единственно.
Предположим, что существует ещё одно выражение для  .
.
 =
=  *
*  + … +
+ … + 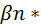

 = (
= ( 
 + … + (
+ … + (  )
) 
Т.к.  …
…  – ЛНЗ
– ЛНЗ
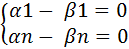 Þ
Þ 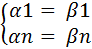
Выражение для  и
и  – одинаковые.
– одинаковые.
6. Геометрический смысл линейной зависимости (ЛЗ) (коллинеарность)
Геометрический смысл линейной зависимости
Определение.
 – коллинеарные, если они параллельны одной прямой (
– коллинеарные, если они параллельны одной прямой ( 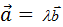 )
)
Утверждение 1.
 – коллинеарные тогда и только тогда, когда они ЛЗ
– коллинеарные тогда и только тогда, когда они ЛЗ
(необходимость) => дано: .  – кол. =>
– кол. =>  , 1
, 1 
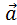 -
-  =0 => .
=0 => .  - ЛЗ
- ЛЗ
(Т.к. нетривиальная комбинация)
(достаточность)<= дано  - ЛЗ =>
- ЛЗ => 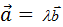 =>
=>  коллинеарные.
коллинеарные.
| M |
| N |
| O |
O, M, N не лежат на одной прямой.
 – неколлинеарные, значит мы не сможем выразить один через другой => ЛНЗ
– неколлинеарные, значит мы не сможем выразить один через другой => ЛНЗ
Утверждение 3.
Любые 3 вектора на плоскости ЛЗ.
Случай 1. Если среди этих векторов есть 2 коллинеарных, то система ЛЗ.
 ,
,  ,
,  .
.
Случай 2. Векторы  – попарно неколлинеарные.
– попарно неколлинеарные.

7. Геометрический смысл линейной зависимости (ЛЗ) (компланарность)

Компланарными называют векторы одной плоскости
3 компланарных вектора – ЛЗ. 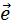 = α2
= α2  + α1
+ α1 
Определение.
Векторы  называются комланарными, если они параллельны одной плоскости.
называются комланарными, если они параллельны одной плоскости.
Утверждение 4.
Три вектора компланары тогда и только тогда, когда они ЛЗ.
 – компланарны
– компланарны 
 – ЛЗ.
– ЛЗ.
 дано:
дано:  компланарны. Значит их можно параллельным переносом перенести в одну плоскость.
компланарны. Значит их можно параллельным переносом перенести в одну плоскость.
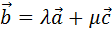 ,
, 
 дано:
дано:  - ЛЗ. Значит один из них можно выразить через остальные. Тогда геометрическая конструкция, связывающая векторы – параллелограмм, а параллелограмм принадлежит плоскости.
- ЛЗ. Значит один из них можно выразить через остальные. Тогда геометрическая конструкция, связывающая векторы – параллелограмм, а параллелограмм принадлежит плоскости.
Значит все векторы принадлежат одной плоскости, т.е. они компланарны.
Утверждение 5.
В пространстве существует три ЛНЗ вектора.
Рассмотрим точки O, M, N, K, не принадлежащие одной плоскости
| K |
| M |
| N |
| О |
 не являются компланарными, значит эта совокупность векторов не является ЛЗ, значит эти векторы ЛНЗ.
не являются компланарными, значит эта совокупность векторов не является ЛЗ, значит эти векторы ЛНЗ.
Утверждение 6.
Любые 4 вектора в пространстве – ЛЗ.
(Доказать самостоятельно!)
|
из
5.00
|
Обсуждение в статье: Понятие линейной зависимости (независимости) векторов. Свойства ЛЗ, ЛНЗ. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

