ТЕПЛОСИЛОВЫЕ ПАРОВЫЕ ЦИКЛЫ

В современной стационарной теплоэнергетике в ос­новном используются паровые теплосиловые установки. Теплосиловые установки, в которых в качестве рабочего тела применяется пар, имеют некоторые особенности и преимущества, существенно отличающие их от теплосиловых установок с газообразным рабочим телом.

Наиболее распространенным рабочим телом теплосиловых паровых циклов является вода — самое доступное и дешевое рабочее тело. Спе­цифические требования к рабочим телам паросиловых установок сфор­мулированы в § 11.6 на основе анализа способов повышения эффектив­ности циклов этих установок. Пока отметим лишь желательность того, чтобы при атмосферном давлении и комнатной температуре рабочее те­ло находилось в жидком состоянии.

* Напомним, что это уравнение применимо для любых значений p₂/p₁, если газ те­чет в сопле Лаваля.

** Для случая адиабатного истечения в вакуум (р₂=0) из уравнения (7.61) сле­дует, что T₂=0 К, т. е. газы на выходе из сопла имеют температуру абсолютного нуля. Это означает, что вся энтальпия газа.полностью превращается в кинетическую энергию потока газа.

 

ЦИКЛ КАРНО

Использование рабочего тела, изменяющего в тече­ние цикла свое агрегатное состояние, позволяет осуществить на практи­ке цикл Карно.

Напомним, что цикл Карно состоит из двух адиабат и двух изотерм. Практически осуществление адиабатных процессов не представляет особых трудностей. Отклонения реальных адиабатных процессов рас­ширения и сжатия от изоэнтропы, обусловленные необратимостью про­цессов течения, конечно, приводят к уменьшению термического КПД цикла, однако это уменьшение не слишком велико.

Практическое осуществление изотермических процессов подвода и отвода теплоты в газовых теплосиловых установках сопряжено с непре­одолимыми трудностями. Как было показано в § 7.9 и в гл. 10, для того чтобы по возможности приблизить реальные процессы к изотермичес­ким, применяют многоступенчатое сжатие воздуха с промежуточным охлаждением (в компрессорах) и ступенчатый подвод теплоты (в газо­турбинных установках).

Совершенно иначе обстоит дело в паросиловых циклах.

В случае потока вещества технически наиболее просто осуществи­мым процессом подвода или отвода теплоты является изобарный про­цесс. Ранее были рассмотрены условия протекания изобарного процесса подвода или отвода теплоты при постоянной температуре. Это — про­цесс фазового перехода чистого вещества из жидкого в газообразное состояние. В самом деле, внутри двухфазной области состояний чистого вещества изобары совпадают с изотермами; следовательно, изобарный процесс подвода теплоты к влажному пару (т.е. парообразование), равно как и изобарный процесс отвода теплоты от влажного пара (т. е. конденсация), легко осуществимые на практике, представляют собой в то же время изотермические процессы. Отсюда следует, что если ис­пользовать влажный пар в качестве рабочего тела и осуществить цикл, составленный из двух адиабат и двух изобар (которые в то же время являются изотермами), то это и будет цикл Карно.

Схема теплосиловой установки, в которой осуществляется цикл Кар­но на влажном паре, представлен на рис. 11.1. В паровой котел 1 посту­пает влажный водяной пар малой степени сухости х. За счет сгорания в топке котла топлива (уголь, мазут, природный газ и др.) к влажно­му пару подводится теплота, и степень сухости пара повышается до значений х, близких к единице. Процесс подвода теплоты в котле про­исходит при постоянном давлении pi и при постоянной температуре Т₁.

Из котла пар поступает в паровую турбину 2. При расширении в турбине поток пара приобретает значительную кинетическую энергию. На лопатках рабочего колеса турбины эта энергия превращается в ки­нетическую энергию вращения рабочего колеса и затем в электроэнер­гию с помощью электрогенератора 3, вращаемого турбиной.

На выходе из турбины влажный пар имеет давление p₂ и соответ­ствующую этому давлению температуру Т₂. Далее пар поступает в кон­денсатор 4 — теплообменник, в котором с помощью охлаждающей воды от пара отводится теплота, пар конденсируется и, следовательно, сте­пень его сухости уменьшается.

Процесс отвода теплоты от пара в конденсаторе осуществляется при постоянном давлении.

После конденсатора влажный пар поступает в компрессор 5, в кото­ром он адиабатно сжимается до давления p₁. Затем влажный пар вновь поступает в котел, и цикл замыкается.

Таким образом, на участке цикла от выхода из компрессора до вхо­да в турбину давление рабочего тела равно p₁, а на участке цикла от выхода из турбины и до входа в компрессор давление рабочего тела равно p₂; конечно, вследствие неизбежных гидравлических потерь при течении пара в трубопроводах давление вдоль потока пара несколько

 

 

 

снижается, но этими потерями напора в первом приближении можно пренебречь.

Описанный цикл изображен в ρ,υ- и Т, s-диаграммах на рис. 11.2.

Подвод теплоты q₁ к пару в котле осуществляется по изобаре-изо­терме 4-1, процесс расширения в паровой турбине — по адиабате 1-2, отвод теплоты q₂ в конденсаторе — по изобаре-изотерме 2-3, сжатие па­ра в компрессоре — по адиабате 3-4. При расширении по адиабате от состояния вблизи правой пограничной кривой степень сухости пара уменьшается; при адиабатном сжатии в состоянии вблизи левой погра­ничной кривой влажность пара возрастает. Отвод теплоты в конденса­торе должен осуществляться до тех пор, пока влажный пар не достиг­нет состояния, которое определяется следующим условием: при сжатии по адиабате от состояния 3 с давлением р₂ до давления p₁ конечное со­стояние рабочего тела не должно оказаться за пределами области на­сыщения.

Термический КПД обратимого цикла Карно, осуществляемого во влажном паре, как и цикла Карно с любым другим рабочим телом, определяется уравнением (3.32):

Реальный цикл, осуществляемый во влажном паре и составленный из двух изобар-изотерм и двух адиабат, условно изображен в Т, s-диаграмме на рис. 11.3 с учетом необратимых потерь на трение при расши­рении пара в турбине и при его сжатии в компрессоре. Здесь S₂—S₁ — увеличение энтропии пара в процессе адиабатного расширения, обуслов­ленное трением, а S₄—S₃ — увеличение энтропии пара при его сжатии в компрессоре.

Из сказанного выше следует, что осуществление цикла Карно во влажном паре вполне возможно. Поскольку критическая температура воды сравнительно невысока (374,15°С), невелик и интервал темпера­тур между нижней (порядка 25 °С) и верхней (не выше 340—350 °С) температурами цикла, ибо при большем приближении к критической точке, резко сужается длина изобарно-изотермического участка 4-1 и, следовательно, относительно большую роль начинают играть снижаю­щие термический КПД цикла неизоэнтропные участки 1-2 и 3-4; степень заполнения цикла уменьшается (рис. 11.3). Однако даже в этом срав­нительно узком интервале предельных температур величина η_т для об­ратимого цикла Карно, осуществляемого во влажном паре, оказывается весьма значительной:

C учетом условий работы теплосило­вого оборудования практическое осуще­ствление этого цикла нецелесообразно, так как при работе на влажном паре, который представляет собой поток сухого насыщен­ного пара со взвешенными в нем капелька­ми воды, условия работы проточных частей турбин и компрессоров оказываются тяжелыми, течение — газодинамически несовершенным и внутренний относи­тельный КПД этих машин η_0i снижается.

Вследствие этого внутренний абсолютный КПД цикла η_i = η_т η_0i оказывается сравнительно малым.

Важно и то, что компрессор для сжатия влажного пара с малыми давлениями и большими удельными объемами представляет собой весь­ма громоздкое, неудобное в эксплуатации устройство, на привод кото­рого затрачивается чрезмерно большая энергия.

По этим причинам цикл Карно, осуществляемый во влажном паре, не нашел практического применения.

 

 

ЦИКЛ РЕНКИНА

Перечисленные выше недостатки, присущие пароси­ловой установке, в которой осуществляется цикл Карно на влажном паре, могут быть частично устранены, если отвод теплоты от влажного пара в конденсаторе производить до тех пор, пока весь пар полностью не сконденсируется.

В этом случае сжатию от давления p₂ до давления p₁ подлежит не влажный пар малой плотности, а вода. По сравнению с удельным объ­емом влажного пара в точке 3 (см. Т, s-диаграмму на рис. 11.2) удель­ный объем воды весьма мал, а ее сжимаемость пренебрежимо мала по сравнению со сжимаемостью влажного пара. Для перемещения воды, из конденсатора в котел с одновременным повышением ее давления при­меняются не компрессоры, а насосы, компактные и простые по устрой­ству, потребляющие весьма мало энергии для своего привода.

Такой цикл предложен в 50-х годах прошлого века почти одновре­менно шотландским инженером и физиком У. Ренкиным и Р. Клау-зиусом; обычно этот цикл называют циклом Ренкина. Схема теплосило­вой установки с циклом Ренкина аналогична схеме установки, изобра­женной на рис. 11.1, с той лишь разницей, что в схеме, работающей по циклу Ренкина, 5 — не компрессор влажного пара, а водяной насос.

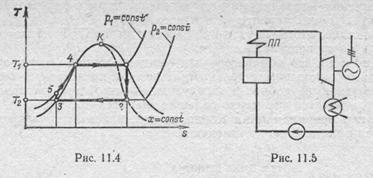
Цикл Ренкина в Т, s-диаграмме изображен на рис. 11.4. Влаж.ный пар в конденсаторе полностью конденсируется по изобаре p2=const (точка 3 на рис. 11.4). Затем вода сжимается насосом от давления р₂ до давления р₁, этот адиабатный процесс изображен в Т, s-диаграмме вертикальным отрезком 3-5.

Длина отрезка 3-5 в Т, s-диаграмме весьма мала; как уже отмеча­лось в гл. 6, в области жидкости изобары в Г, s-диаграмме проходят очень близко друг от друга. Благодаря этому при изоэнтропном сжатии воды, находящейся при температуре 25 °С и давлении насыщения 3,1 кПа (0,032 кгс/см2), до давления 29400 кПа (300 кгс/см2) темпера­тура воды возрастает менее чем на 1 °С, и можно с хорошей степенью приближения считать, что в области жидкости изобары воды практи­чески совпадают с левой пограничной кривой; поэтому зачастую при изображении цикла Ренкина в Т, s-диаграмме изобары в области жид­кости изображают сливающимися с левой пограничной кривой.

Малая длина отрезка адиабаты 3-5 свидетельствует о малой работе, затрачиваемой насосом на сжатие воды. Малая работа сжатия по сравнению с работой, производимой водяным паром в процессе расширения 1-2, является важным преимуществом цикла Ренкина.

Напомним, что, как показано в § 5,9 применительно к сжатию газа в компрессоре, работа, затрачиваемая на собственно сжатие газа от давления р₂ до давления р₁, опре­деляется соотношением (7.188), которое для 1 кг рабочего тела запишется следующим образом:

 

 

[так как υ(p₁)< υ (p₂), то l_2-1<0]. а работа, затрачиваемая на осуществление всего цикла компрессора (так называемая техническая работа сжатия) определяется соотно­шением (7.196а):

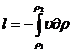
Напомним также, что для адиабатного сжатия в соответствии с уравнением (8.15)

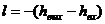
где h_вых и h_вx — энтальпия сжимаемого газа после сжатия на выходе из компрессора (давление р₁) и до сжатия (давление р₂).

Уравнения (7.188) и (7.196а) не зависят от вида сжимаемого вещества; разумеется, они в полной мере справедливы и для сжатия жидкости с помощью насоса.

В первом приближении, вполне достаточном для технических расчетов, воду мож­но считать практически несжимаемой (υ_B=const, т. е. d υ_B =0) и, следовательно, lсж=0.

Техническую работу насоса получаем, вынося в уравнении (7.196а) величину υ_B за знак интеграла:

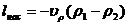
(11.1)

(знак минус показывает, что работа должна быть подведена к насосу извне).

Техническая работа насоса, сжимающего воду, также весьма мала; например, ес­ли вода сжимается от давления р₂=3,1 кПа (0,032 кгс/см2) до давления p₁=49030 кПа (500 кгс/см2), то, как показывает расчет по уравнению (11.1):

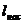= 49,0 кДж/кг (11,7 ккал/кг)*.

Этот же результат можно получить, используя уравнение (8.15). Для этого с по­мощью h, s-диаграммы или таблиц термодинамических свойств водяного пара нужно найти разность энтальпий воды на данной изоэнтропе при давлениях р₁ и р₂.

 

Из насоса вода под давлением p1 поступает в котел, где к ней в изобарном процессе p₁=const подводится теплота. Вначале вода в котле нагревается до кипения (участок 5-4 изобары p₁=const на рис. 11.4), а затем, по достижении температуры кипения, происходит процесс парообразования (участок 4-1 изобары p₁=const на рис. 11.4). Сухой насыщенный пар, получаемый в котле, поступает в турбину; про­цесс расширения в турбине изображается адиабатой 1-2. Отработанный влажный пар поступает в конденсатор, и цикл замыкается.

В отношении термического КПД цикл Ренкина представляется ме­нее выгодным, чем обратимый цикл Карно, изображенный на рис. 11.2, поскольку степень заполнения цикла (равно как и средняя температу­ра подвода теплоты) для цикла Ренкина оказывается меньше, чем для цикла Карно. Однако с учетом реальных условий осуществления цикла и значительно меньшего влияния- необратимости процесса сжатия воды по сравнению со сжатием влажного пара на общий КПД цикла эконо­мичность цикла Ренкина выше экономичности соответствующего цикла Карно во влажном паре. Вместе с тем замена громоздкого компрессора

* Отметим, что для сжатия идеального газа в том же интервале давлений нужно

затратить во много раз большую работу [например, для идеального газа с k=1,4 и R = 490 Дж/(кг-К) работа сжатия составит 5380 кДж/кг (1285 ккал/кг)].

 

для сжатия влажного пара компактным водяным насосом позволяет существенно снизить затраты на сооружение теплосиловой установки и упростить ее эксплуатацию.

Благодаря отмеченным обстоятельствам внутренние абсолютные КПД сравниваемых циклов будут примерно одинаковыми.

Для того чтобы увеличить термический КПД цикла Ренкина, приме­няют так называемый перегрев пара в специальном элементе кот­ла— пароперегревателе (ПП на рис. 11.5), где пар нагревается до температуры, превышающей температуру насыщения при данном давлении p₁. Цикл Ренкина с перегретым паром в Т, s-диаграмме пока­зан на рис. 11.6. В этом случае средняя температура подвода теплоты увеличивается по сравнению с температурой подвода теплоты в цикле без перегрева и, следовательно, термический КПД цикла возрастает.

Из рис. 11.6 видно, что для цикла с перегревом процесс расширения пара в турбине 1-2, осуществляемый до того же, что и раньше, давле­ния р₂, заканчивается внутри двухфазной области в районе более высо­ких степеней сухости, чем для цикла, изображенного на рис. 11.4. Бла­годаря этому условия работы проточной части турбины оказываются более легкими и, следовательно, повышаются внутренний относительный КПД турбины η_0i и внутренний КПД цикла η_i; величина η_i для цикла с перегревом возрастает за счет роста η_T, так и η_0i.

Цикл Ренкина с перегревом пара является основным циклом тепло­силовых установок, применяемых в современной теплоэнергетике.

Количество теплоты q₁ подводимой к рабочему телу в цикле, изоб­ражается в Т, s-диаграмме на рис. 11.6 площадью а-3-5-4-6-1-b-а. Теп­лота q₂, отводимая в цикле, эквивалентна площади а-З-2-b-a, а работа цикла — площади 3-5-4-6-1-2-3.

Поскольку процессы подвода и отвода теплоты в цикле Ренкина осуществляются по изобарам, а в изобарном процессе количество под­веденной (отведенной) теплоты равно разности энтальпий рабочего те­ла в начале и конце процесса, применительно к циклу Ренкина имеем

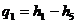
(11.2)

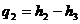
(11.3)

(индексы у величин h соответствуют обозначениям состояний рабочего тела на рис. 11.6).

Здесь h₁ — энтальпия перегретого водяного пара на выходе из кот­ла* (при давлении p₁ и температуре T₁); h₅ — энтальпия воды на входе в котел, т. е. на выходе из насоса (при давлении p₁ и температуре Т₅); h₂— энтальпия влажного пара на выходе из турбины, т.е. на входе в конденсатор (при давлении р₂ и степени сухости х), a h₃ — энтальпия

 

*Предполагается для простоты, что на пути от котла до турбины давление и тем­пература не изменяются. В действительности из-за гидравлического сопротивления па­ропровода и неизбежных теплопотерь давление и температура пара несколько снижа­ются.

 

воды на выходе из конденсатора (она равна энтальпии воды на линии насыщения h' при температуре насыщения Т₂, однозначно определяе­мой давлением p₂).

С учетом этих соотношений получаем из общего уравнения для тер­мического КПД цикла применительно к обратимому циклу Ренкина:

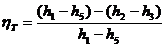
Это уравнение может быть записано в следующем виде:

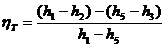
Разность h₁ — h₂ представляет собой располагаемый перепад энталь­пий, превращаемый в кинетическую энергию потока и затем в работу в турбине, разность же h₅ — h₃ — это в соответствии с (8.15) техничес­кая работа насоса. Таким образом, работу, производимую в цикле, мож­но рассматривать как разность работы, полученной в турбине, и работы, затрачиваемой на привод насоса.

Условимся в дальнейшем обозначать:

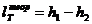
(11.5)

(11.6)

тогда

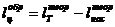
(10.17)

индексы «теор» и «обр» показывают, что эти величины относятся к тео­ретическому обратимому циклу без учета потерь, обусловленных необ­ратимостью реальных процессов; индекс «т» — величины относятся к турбине.

Не следует смешивать величину 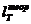с работой расширения, а 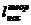— с рабо­той сжатия в цикле. На рис. 11.7 цикл Ренкина изображен в р, υ-диаграмме (обозна­чения те же, что и на рис. 11.6). В этой диаграмме 5-4-6-1 — изобара p₁= const, по кото­рой осуществляется подвод теплоты в цикле; 1-2 — адиабата расширения пара в тур­бине; 2-3 — изобара p₂=const отвода теплоты в конденсаторе и 3-5 — адиабата сжатия воды в насосе (вследствие малой сжимаемости воды эта адиабата практически совпа­дает с изохорой). Как видно из этой диаграммы, работа расширения равна площади c-5-1-2-d-c, работа сжатия — площади с-З-2-d-c и работа цикла — площади 1-2-3-5-1.

Что же касается величин 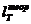=h₁–h₂ и 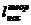=h₅ – h₃, то они изображаются в

р, υ-диаграмме следующим образом. В соответствии с уравнением (8.15) h₁ – h₂ изобра­жается площадью l-2-m-n-l. Разность h₅ — h₃ согласно (7.196а) изображается площадь 5-3-m-n-5. Отсюда следует, что работа цикла, равная разност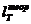и и 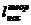, изображается площадью 1-2-3-5-1,

 

С учетом уравнения (11.1) для технической работы насоса

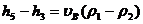
(11.8)

соотношение (11.4а) запишется в виде

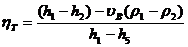
(11.9)

Уравнения (11.4а) и (11.9) позволяют с помощью h, s-диаграммы или таблиц термодинамических свойств воды и водяного пара опреде­лить величину термического КПД обратимого цикла Ренкина по извест­ным значениям так называемых начальных параметров пара (т. е. пара­метров пара на входе в турбину) при p₁ и T₁ и давления пара в кон­денсаторе.

Так, если в турбину поступает пар с давлением p₁=16670 кПа . (170 кгс/см2) и температурой T₁ =550 °С, а давление пара в конденсаторе поддерживается равным р₂=4 кПа (0,04 кг/см2), то расчет значения η_T цикла Ренкина ведется следующим

 

 

образом. Из таблиц термодинамических свойств воды и водяного пара находим*, что энтальпия пара при давлении 16670 кПа (170 кгс/см²) и температуре 550 °С составляет h₁=3438 кДж/кг (821,2ккал/кг), энтропия пара при этом равна S₁=6,4619 кДж/(кгК) [1,5434 ккал/(кгК)]. С помощью h, s-диаграммы (или же расчетным путем) находим значение энтальпии влажного пара h2 при давлении р₂=4 кПа (0,04 кгс/см²) и том же, что я в точке 1, значении энтропии (в обратимом процессе адиабата расширения совпа­дает с изоэнтропой). Эта величина равна h₂=1945 кДж/кг(464,5 ккал/кг).

Энтальпия воды на линии насыщения при давлении р₂=4 кПа (0,04 кгс/см²) равна h₃=120 кДж/кг (28,7 ккал/кг). Энтропия воды в этом состоянии равна 0,4178 кДж/ (кгК) [0,0998 ккал/(кгК)]. Находим с помощью таблиц свойств воды и водяного пара значение энтальпии воды в точке 5, на выходе из насоса, при давлении 16670 кПа (170 кгс/см²) и том же, что и в точке 3, значении энтропии: h₅ =137 кДж/кг (32,7 ккал/кг) (при этом температура воды T₅=29°С).

Таким образом, h₁—h₂=1493 кДж/кг (356,7 ккал/кг); h₅—h₃=17 кДж/кг (4,0 ккал/кг); h₁—h₅=3301 кДж/кг (788,5 ккал/кг). Подставляя эти значения в уравне­ние (11,4а), получаем, что термический КПД рассматриваемого обратимого цикла Ренкина составляет η_T=0,46. Укажем для сравнения, что термический КПД обратимо, го цикла Карно, осуществляемого в том же интервале температур (550 °С—28,6 °С), составляет η^о.ц.к=0,63, т. е. значительно выше, чем подсчитанный нами КПД обрати­мого цикла Ренкина.

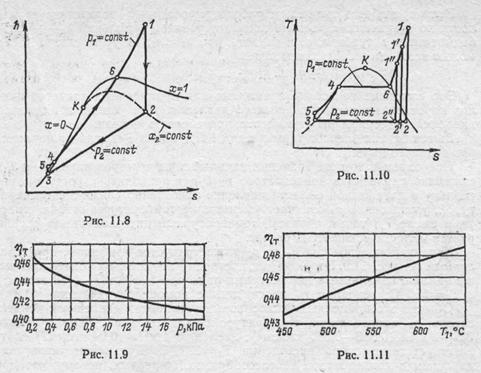
На рис. 11.8 цикл Ренкина изображен в h, s-диаграмме (обозначе­ния состояний те же, что и на Т, s- и р, υ-диаграммах на рис. 11.6 и 11.7). Очевидно, что в соответствии с уравнением (11.4а) в этой диа­грамме, расстояние по ординате между точками / и 2 соответствует ра­боте, производимой турбиной, расстояние между точками 5 и 3 — рабо­те, затрачиваемой в насосе, расстояние между точками / и 5 — теплу q\, подводимому в цикле, а между точками 2 и 3 — теплу qz, отводимому в цикле.

* Рассматриваемый пример относится к циклу с реальной паротурбинной установ­кой, имеющей начальные параметры p₁ = 170 кгс/см² и T₂=550˚С при давлении в кон­денсаторе p₂=0,04 кгс/см². В этой связи используемые в расчете значения h и s бра­лись из таблиц термодинамических свойств воды и водяного пара, составленных по круглым значениям давлений, выраженных в кгс/см² [в этом случае в современных таблицах свойств воды и водяного пара значения h и s приводятся соответственно в ккал/кг и ккал/(кгК)], а затем переводились в: единицы СИ. Сказанное относится и к примеру, рассматриваемому в § 11.3

 

Если пренебречь значением работы насоса h₅ — h₃ вследствие ее ма­лости по сравнению с располагаемым перепадом энтальпий h₁—h₂, сра­батываемым в турбине, т.е. считать, что h₃≈h₅, то уравнение (11.4а) можно записать в следующем виде:

(11.10)

 

Это соотношение вполне приемлемо для прикидочных расчетов цик­лов паросиловых установок низкого давления. Для установок высокого давления значением работы насоса пренебрегать нельзя.

Выясним, как зависит термический КПД цикла Ренкина от парамет­ров водяного пара.

При одном и том же значении начальных параметров пара (p₁ и T₁) снижение давления в конденсаторе р₂ будет приводить к росту η_T: по­скольку в двухфазной области давление однозначно связано с темпера­турой, уменьшение p₂ означает уменьшение температуры отвода тепло­ты в цикле Т₂, таким образом, температурный интервал цикла расши­ряется и термический КПД растет.

Характер зависимости η_T от р2 иллюстрируется графиком, представ­ленным на рис. 11.9. Этот, график построен для уже рассмотренного вы­ше цикла с начальными параметрами пара p₁ = 16670 кПа (170 кгс/см²) и T₁=550°С; значения η_T подсчитаны с помощью уравнения (11.4а).

Обычно в современных теплосиловых установках давление в конден­саторе р₂ определяется температурой охлаждающей воды и равно 3,5—4 кПа (0,035—0,040 кгс/см²); давлению 4 кПа (0,04 кгс/см2) соот­ветствует температура насыщения T₂=28,6°С. Дальнейшее снижение давления в конденсаторе нецелесообразно, во-первых, потому, что при более глубоком разрежении возрастает удельный объем пара, поступа­ющего из турбины в конденсатор, вследствие чего размеры конденсато­ра и последних ступеней турбины увеличиваются. Во-вторых, при более глубоком разрежении температура влажного пара в конденсаторе по­лучается более низкой (при давлении 3 кПа температура насыщения воды равна 23,8 °С, а при давлении 2 кПа — соответственно 17,2 °С), вследствие чего разность температур конденсирующегося пара и омы­вающей конденсатор охлаждающей воды * становится слишком малой, что лриводит к увеличению размеров конденсатора.

Термический КПД цикла Ренкина зависит, однако, в первую очередь от начальных параметров пара (р₁, T₁). С ростом температуры перегре­ва пара T₁ при одном и том же давлении термический КПД цикла уве­личивается, так как возрастает средняя температура подвода теплоты в цикле (рис. 11.10). В качестве примера на рис. 11.11 приведен график зависимости η_T от T₁ для цикла Ренкина, в котором начальное давление пара р₁ = 16670 кПа (170 кгс/см²), а давление пара в конденсаторе р2=4 кПа (0,04 кгс/см²).

Если верхняя температура в цикле T₁ постоянна, то повышение дав­ления пара p₁ также приводит к росту термического КПД цикла: чем выше р1 тем больше степень заполнения цикла и выше средняя темпе­ратура подвода теплоты (рис. 11.12).

Однако по мере роста р₁ при той же температуре перегрева влаж­ность пара по выходе из турбины возрастает, что влечет за собой умень­шение η_0i турбины. Поэтому при увеличении начального давления же­лательно также увеличить температуру пара перед турбиной. На рис. 11.13 приведен график зависимости η_T от р1 для цикла Ренкина при T₁ = 550˚С и р₂= 4 кПа (0,04 кгс/см²).

Из сказанного выше очевидно, что чем выше давление пара pi и тем­пература T₁, тем выше термический КПД цикла Ренкина. На рис. 11.14 приведена зависимость η_T обратимого цикла Ренкина от p₁ для разных значений Т₁.

* Охлаждающая вода подается в конденсатор из рек, прудов или градирен; по­нятно, что температура этой воды зависит от климатических условий и колеблется в течение .года; в принципе она может изменяться от 0 до 25—30 °С.

 

 

 

Таким образом, для увеличения термического КПД цикла Ренкина в принципе следует стремиться к повышению начальных параметров пара.

В настоящее время на электростанциях СССР используется в основном пар с ос­новными параметрами p₁=23500 кПа (240 кгс/см²) T₁=565°C. Имеются опытные установки с параметрами пара p₁=29400 кПа (300 кгс/см²) и с начальной температу­рой не выше

T₁=600–650 ˚С.

Дальнейшее повышение начальных параметров пара ограничивается свойствами существующих конструкционных материалов: при высоких давлениях и температурах прочностные характеристики перлитных сталей ухудшаются и их приходится заменять значительно более дорогостоящими аустенитными сталями. Хотя при этом за счет повышения р₁ и Т₁ термический КПД цикла несколько возрастает, но увеличиваются и капитальные затраты на сооружение установки, иными словами, достигается эконо­мия топлива, но увеличивается расход дорогостоящих сортов металла. С этой точки зрения дальнейшее повышение начальных параметров пара, особенно в районах с де­шевым топливом, оказывается нецелесообразным. Этот вопрос решается на основе всестороннего технико-экономического анализа