 |
Главная |
Равновесие тел под действием произвольной плоской системы сил
|
из
5.00
|
ОГЛАВЛЕНИЕ
Предисловие ……………………………………………………………………………..4
Часть первая. СТАТИКА
Плоская система сил.
Равновесие твердых тел под действием произвольной плоской системы
сил……………………………………………………………………………………….. 5
1.2. Равновесие твердых тел под действием произвольной пространственной системы сил…………………………………………………………………………….14
1.3. Равновесие при наличии трения………………………………………………..23
1.4. Приведение произвольной системы сил к простейшему виду……………..31
1.5. Центр тяжести……………………………………………………………………..38
Часть вторая. КИНЕМАТИКА
2.1. Кинематика точки………………………………………………………………...45
2.2. Простейшие движения твердого тела…………………………………………..53
2.3. Сложное движение точки…………………………………………………...……61
2.4. Плоское движение твердого тела……………………………………………….68
2.5. Сложение вращений………………………………………………………………80
2.6. Сферическое движение твердого тела………………………………………….93
Часть третья. ДИНАМИКА
3.1. Динамика материальной точки………………………………………………..
3.2. Прямолинейные колебания точки…………………………………………….
Движение центра масс и изменение количества движения механичес-
кой системы…………………………………………………………………………..
3.4. Изменение кинетического момента механической системы ……………..
3.5. Изменение кинетической энергии механической системы……………….
3.6. Смешанные задачи……………………………………………………………..
3.7. Тензор инерции…………………………………………………………………
3.8. Принцип д Аламбера. Определение динамических реакций…………….
3.9. Общие теоремы динамики при ударе……………………………………….
Часть четвертая. АНАЛИТИЧЕСКАЯ МЕХАНИКА
4.1 Принцип виртуальных перемещений………………………………………
4.2. Общее уравнение динамики. Уравнения Лагранжа второго рода……
4.3. Малые колебания систем с одной степенью свободы……………………..
4.4. Малые колебания систем с двумя степенями свободы………………
ПРЕДИСЛОВИЕ
Основным задачником в преподавании теоретической механики является на протяжении многих лет (и будет являться таковым в обозримом будущем) сборник задач И.В.Мещерского [1]. Тем не менее потребность в издании новых задачников существует. Уже в третьем издании вышел сборник задач под общей редакцией Колесникова К.С. [2], подготовленный преподавателями Московского государственного технического университета им. Н.Э.Баумана. Вышла серия руководств по решению задач и сборников заданий для курсовых работ [3-11]. Отличительной особенностью данного задачника является включение в него кратких необходимых сведений из теоретической части курса, примеров решения задач по всем разделам и необходимое количество типовых задач для организации аудиторной работы и выполнения домашних заданий. В каждом разделе представлены тематические задачи с техническим содержанием, облегчающим переход к изучению последующих общепрофессиональных и специальных дисциплин.
Предлагаемое учебное пособие ориентировано на организацию аудиторной и самостоятельной учебной работы по всем машиностроительным специальностям с числом часов, отводимым на изучение курса, в размере порядка 200 часов в течение двух семестров.
В основу учебного пособия положен опыт организации учебного процесса по теоретической механике для машиностроительных специальностей в Уральском государственном техническом университете имени Первого Президента России Б.Н. Ельцина.
Часть 1. Статика
Равновесие тел под действием произвольной плоской системы сил
Для равновесия тела под действием произвольной плоской системы сил необходимо и достаточно, чтобы сумма проекций всех сил на каждую из координатных осей и сумма моментов сил относительно произвольной точки равнялись нулю:
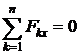 ,
, 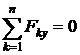 ,
,  .
.
Условие равновесия тела под действием плоской системы сил может быть записано в следующих эквивалентных формах:
 ,
,  ,
, 
(отрезок  не перпендикулярен оси
не перпендикулярен оси  , при этом исключается случай приведения системы сил к равнодействующей, проходящей через точки
, при этом исключается случай приведения системы сил к равнодействующей, проходящей через точки  и
и  );
);
 ,
,  ,
, 
(точки A, B, C не лежат на одной прямой, при этом исключается случай приведения системы сил к равнодействующей, проходящей через точки A, B и C).
Если в равновесии находится не одно тело, а система тел, то для определения всех неизвестных величин необходимо расчленять систему, вводя в рассмотрение реакции внутренних связей.
 Пример 1.1.1.Определить реакции опор в точках А и В балки (рис. 1.1.1), находящейся под действием сосредоточенной силы Р = 6 кН и пары сил с моментом М = 3 кН·м, если АВ = 3 м; ВС = 2 м. Весом балки пренебречь.
Пример 1.1.1.Определить реакции опор в точках А и В балки (рис. 1.1.1), находящейся под действием сосредоточенной силы Р = 6 кН и пары сил с моментом М = 3 кН·м, если АВ = 3 м; ВС = 2 м. Весом балки пренебречь.
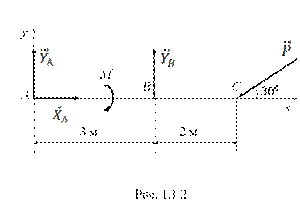 Решение:
Решение:
1. Рассмотрим равновесие балки, мысленно освобождая ее от связей (неподвижной шарнирной опоры в точке А и подвижной шарнирной опоры в точке В).
2. Изобразим заданные силы и реакции связей  (рис. 1.1.2).
(рис. 1.1.2).
3. Используя условия равновесия балки в форме
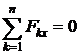 ,
, 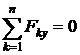 ,
,  ,
,
имеем
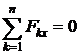 ,
,  ,
,
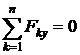 ,
, 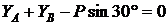 ,
,
 ,
,  .
.
Откуда
 ,
, 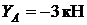 ,
, 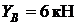 .
.
Знак «минус» означает, что истинное направление соответствующей реакции противоположно выбранному при решении задачи.
 Пример 1.1.2.Определить реакции внешних (в точках A и E) и внутренней (в точке C) связей составной рамы (рис. 1.1.3), находящейся под действием сосредоточенных сил Р1 = 12 кН, Р2 = 10 кН и пары сил с моментом М = 16 кН∙м. Весом рамы пренебречь.
Пример 1.1.2.Определить реакции внешних (в точках A и E) и внутренней (в точке C) связей составной рамы (рис. 1.1.3), находящейся под действием сосредоточенных сил Р1 = 12 кН, Р2 = 10 кН и пары сил с моментом М = 16 кН∙м. Весом рамы пренебречь.
Решение:
1. Рассмотрим равновесие левой части рамы, мысленно освобождая ее от связей (подвижной шарнирной опоры в точке А и неподвижной шарнирной опоры в точке С).
2.  Изобразим заданные силы и реакции внешней и внутренней связей, приложенные к левой части рамы (рис. 1.1.4).
Изобразим заданные силы и реакции внешней и внутренней связей, приложенные к левой части рамы (рис. 1.1.4).
3. Используя условия равновесия левой части рамы в форме
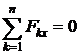 ,
, 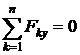 ,
,  ,
,
имеем
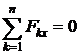 ,
,  ,
,
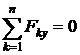 ,
,  ,
,
 ,
,  .
.
Откуда
 ,
,  ,
,  .
.
4. Рассмотрим равновесие рамы, мысленно освобождая ее от внешних связей (подвижной шарнирной опоры в точке А и жесткой заделки в точке E).
5. Изобразим заданные силы и реакции внешних связей, приложенные к раме (рис. 1.1.5).
6.  Используя условия равновесия рамы в форме
Используя условия равновесия рамы в форме
 ,
, 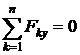 ,
, 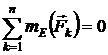 ,
,
имеем
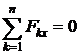 ,
,  ,
,
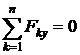 ,
,  ,
,
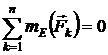 ,
,  .
.
Откуда
 ,
,  ,
,  .
.
Другой, возможный, способ решения заключается в использовании условий равновесия правой части рамы.
Задача 1.1.1. Определить реакции связей в точках А и В балки (рис. 1.1.6), находящейся под действием силы Р = 4 кН и пары сил с моментом М = 6 кН∙м.

 Ответ: XA = –3,46 кH; YA = –6 кH; RB = 8 кH.
Ответ: XA = –3,46 кH; YA = –6 кH; RB = 8 кH.
Задача 1.1.2. Определить реакции опор в точках А и В балки (рис. 1.1.7), находящейся под действием равномерно распределенной нагрузки интенсивности q = 3 кН/м и пары сил с моментом М = 6 кН∙м.
Ответ: XA = 1 кH; YA = 5,20 кH; RB = 4 кH.
Задача 1.1.3. Определить реакции заделки в точке А вертикальной стойки (рис. 1.1.8), находящейся под действием силы Р = 4 кН и пары сил с моментом М = 5 кН∙м.
 Ответ: XA = 2 кH; YA = 3,46 кH; MA = –1 кH.
Ответ: XA = 2 кH; YA = 3,46 кH; MA = –1 кH.
 Задача 1.1.4. Определить реакции заделки в точке А рамы (рис. 1.1.9), находящейся под действием силы Р = 10 кН, пары сил с моментом М = 10 кН∙м и равномерно распределенной нагрузки интенсивности q = 3 кН/м.
Задача 1.1.4. Определить реакции заделки в точке А рамы (рис. 1.1.9), находящейся под действием силы Р = 10 кН, пары сил с моментом М = 10 кН∙м и равномерно распределенной нагрузки интенсивности q = 3 кН/м.
Ответ: XA = –8,66 кH; YA = 1 кH; МА = 23,66 кН×м.
Задача 1.1.5.Определить реакции опор в точках А и D рамы (рис. 1.1.10), находящейся под действием силы Р = 10 кН, пары сил с моментом М = 4 кН∙м и равномерно распределенной нагрузки интенсивности q = 2 кН/м, если  .
.

 Ответ: XA = 7,07 кH; YA = 24,14 кH; RD = 9,07 кH.
Ответ: XA = 7,07 кH; YA = 24,14 кH; RD = 9,07 кH.
Задача 1.1.6.Однородная балка (рис. 1.1.11) длины 6м и веса 160 Н упирается концом в пол и стену, а в промежуточной точке C на ребро. Определить реакции опор в точках А и C, если АD = 2 м.
Ответ: XA = 51,96 H; YA = 130 H; RС = 60 H.
Задача 1.1.7.Однородная балка 1 (рис. 1.1.12) веса 120 Н прикреплена к стене шарниром в точке А и удерживается в указанном положении тросом 2, перекинутым через блок 3. На конце троса подвешен груз 4 веса G. Определить реакции шарнира и вес груза, пренебрегая трением на блоке.
 Ответ: XA = 25,96 H; YA = –15 H; G = 30 H.
Ответ: XA = 25,96 H; YA = –15 H; G = 30 H.
 Задача 1.1.8.Вертикальный стержень 1, прикрепленный шарниром к основанию в точке А (рис. 1.1.13), нагружен силой Р = 10 кН и удерживается в равновесии растяжкой 2. Определить реакции связей, если
Задача 1.1.8.Вертикальный стержень 1, прикрепленный шарниром к основанию в точке А (рис. 1.1.13), нагружен силой Р = 10 кН и удерживается в равновесии растяжкой 2. Определить реакции связей, если  .
.
Ответ: XA = –25 кH; YA = – 25,98 кH; S = –30 кH.
Задача 1.1.9.На вертикальной проволочной полуокружности 1 находится втулка 2 (рис. 1.1.14), соединенная с грузом 5 посредством нити 3, перекинутой через блок 4. Определить угол α, при котором втулка находится в равновесии, и реакцию полуокружности, если вес груза 100 Н, а вес втулки 173 Н. Трением и размерами втулки пренебречь.

 Ответ: N = 100 H; α = 60°.
Ответ: N = 100 H; α = 60°.
Задача 1.1.10.Определить реакции внешних и внутренних связей двухпролетной балки (рис. 1.1.15), находящейся под действием сил Р1 = 22 кН, Р2 = 8 кН и пары сил с моментом М = 20 кН∙м.
Ответ: XА = 19,05 кH; YА = 5 кH; МА = –2 кН∙м; XС = 0 кH; YС = ±6 кH;
YЕ = 14 кH.
Задача 1.1.11.Определить реакции внешних и внутренних связей составной рамы (рис. 1.1.16), находящейся под действием сил Р1 = 8 кН, Р2 = 10 кН и пары сил с моментом М = 30 кН∙м.
Ответ: XF = 6,93 кH; YF = 6 кH; МF = –0,28 кН∙м; XС = ±6,93 кH; YС = ±4 кH;
YВ = 8 кH.

 Задача 1.1.12.Конструкция состоит из стойки 1, балки 2, соединенных шарниром в точке С, и стержня 3 (рис. 1.1.17). На балку 2 действует равномерно распределенная нагрузка интенсивности q = 1 кH/м, а к стойке 1 приложена сила Р = 5 кН. Весом конструкции пренебречь. Определить реакции связей в точках С и D, а также усилие в стержне, если ВС = 3 м, CD = 4 м, DK = КC.
Задача 1.1.12.Конструкция состоит из стойки 1, балки 2, соединенных шарниром в точке С, и стержня 3 (рис. 1.1.17). На балку 2 действует равномерно распределенная нагрузка интенсивности q = 1 кH/м, а к стойке 1 приложена сила Р = 5 кН. Весом конструкции пренебречь. Определить реакции связей в точках С и D, а также усилие в стержне, если ВС = 3 м, CD = 4 м, DK = КC.
Ответ: XD = 4,25 кH; YD = –1,30 кH; МD = –7 кН∙м; XС = ±0,75 кH; YС = ±1,30 кН; S = 12 кH.
 Задача 1.1.13.Однородная балка 1 веса 58 кН, прикрепленная шарниром к стене (рис. 1.1.18), удерживается в равновесии веревкой 2. На балку 1 в точке D опирается однородная балка 3 веса 30 кН. Определить реакции шарниров в точках А и С, натяжение веревки и силу давления балки 3 на балку 1, если
Задача 1.1.13.Однородная балка 1 веса 58 кН, прикрепленная шарниром к стене (рис. 1.1.18), удерживается в равновесии веревкой 2. На балку 1 в точке D опирается однородная балка 3 веса 30 кН. Определить реакции шарниров в точках А и С, натяжение веревки и силу давления балки 3 на балку 1, если  и
и  .
.
Ответ: XА = 0 H; YА = 10 кH; XС = 20,78 кH; YС = 38 кН; Т = 20,78 кН; RD = 20 кН.
 Задача 1.1.14.Однородная балка 1 (рис. 1.1.19) длины 2 м и веса 600 H шарниром прикреплена к вертикальной стене, а в точке В опирается на ребро. Между стеной и балкой зажат цилиндр 2 радиуса 25 см и веса 1 кH. Пренебрегая трением цилиндра о балку и стену, определить реакции шарнира, стены и ребра, а также силу давления цилиндра на балку, если
Задача 1.1.14.Однородная балка 1 (рис. 1.1.19) длины 2 м и веса 600 H шарниром прикреплена к вертикальной стене, а в точке В опирается на ребро. Между стеной и балкой зажат цилиндр 2 радиуса 25 см и веса 1 кH. Пренебрегая трением цилиндра о балку и стену, определить реакции шарнира, стены и ребра, а также силу давления цилиндра на балку, если  .
.
Ответ: XА = –0,24 кH; YА = 1,01 кH; NС = 1,15 кH; ND = 0,58 кН; RВ = 0, 68 кН.
 Задача 1.1.15.В кривошипно–кулисном механизме (рис. 1.1.20), расположенном в вертикальной плоскости, кривошип 1 веса 160 H соединен шарниром в точке B с камнем 2 веса 20 Н, который перемещается по кулисе 3 веса 200 H. К кривошипу 1 приложена пара сил с моментом М = 150 Н∙м.Определить момент L пары, которую нужно приложить к кулисе 3, чтобы механизм находился в покое в положении, указанном на рисунке. Определить в этом положении реакции опор в точках А и С и силу давления камня 2 на кулису 3, если АВ = 0,3 м; СD = 2 м; АС = 0,4 м.
Задача 1.1.15.В кривошипно–кулисном механизме (рис. 1.1.20), расположенном в вертикальной плоскости, кривошип 1 веса 160 H соединен шарниром в точке B с камнем 2 веса 20 Н, который перемещается по кулисе 3 веса 200 H. К кривошипу 1 приложена пара сил с моментом М = 150 Н∙м.Определить момент L пары, которую нужно приложить к кулисе 3, чтобы механизм находился в покое в положении, указанном на рисунке. Определить в этом положении реакции опор в точках А и С и силу давления камня 2 на кулису 3, если АВ = 0,3 м; СD = 2 м; АС = 0,4 м.
Ответ: L = 0,47 кН∙м; XА = 0,40 кH; YА = –0,42 кH; XС = 0,40 кH; YС = 0,50 кH;
RВ = 0,50 кH.
 Задача 1.1.16.Рама 1 (рис. 1.1.21) в точке A заделана в пол, а в точке С соединена шарниром с балкой 2, который удерживается в горизонтальном положении нитью 3, переброшенной через блок 4 и несущей на конце груз 5 веса P. На участке ВD рама и балка нагружены распределенной нагрузкой интенсивности q = 10 кН/м. Определить вес груза, при котором обеспечивается равновесие системы в заданном положении, а также найти реакции заделки и шарнира, если АВ = ВС = 2 СD = 4 м.
Задача 1.1.16.Рама 1 (рис. 1.1.21) в точке A заделана в пол, а в точке С соединена шарниром с балкой 2, который удерживается в горизонтальном положении нитью 3, переброшенной через блок 4 и несущей на конце груз 5 веса P. На участке ВD рама и балка нагружены распределенной нагрузкой интенсивности q = 10 кН/м. Определить вес груза, при котором обеспечивается равновесие системы в заданном положении, а также найти реакции заделки и шарнира, если АВ = ВС = 2 СD = 4 м.
Ответ: Р = 14,1 кН; XА = –10 Н; YА = 50 Н; МА = 80 кН∙м; 
 ;
; 
 .
.

 Задача 1.1.17.Кривошипно–кулисный механизм (рис. 1.1.22), состоящий из кривошипа 3, стержня 2 и кулисы 1, находится в равновесии под действием силы P = 100 Н и уравновешивающей пары с моментом М. Пренебрегая весом звеньев, определить реакции связей в точках А и В, а также момент уравновешивающей пары, если ОА = 10 см, АС = 5 см.
Задача 1.1.17.Кривошипно–кулисный механизм (рис. 1.1.22), состоящий из кривошипа 3, стержня 2 и кулисы 1, находится в равновесии под действием силы P = 100 Н и уравновешивающей пары с моментом М. Пренебрегая весом звеньев, определить реакции связей в точках А и В, а также момент уравновешивающей пары, если ОА = 10 см, АС = 5 см.
Ответ: XА =  10,8 Н; YА =
10,8 Н; YА =  81,25 Н; RВ = 21,65 H; М = 108 Н∙м.
81,25 Н; RВ = 21,65 H; М = 108 Н∙м.
Задача 1.1.18.В четырехзвенном механизме (рис. 1.1.23), находящемся в равновесии, к звену 1 приложена пара сил с моментом М = 300 Н∙м, на звено 2 действует вертикальная сила Р = 100 Н. Пренебрегая весом звеньев, определить величину уравновешивающего момента L, приложенного к звену 3, и реакции шарниров в точках А, В, С и D, если АВ = 0,3 м; ВС = СD = 0,6 м,  .
.
Ответ: XА = 1,18 кH; YА = 0, 05 кH; XВ = XС = ±1,18 кH; YВ = YС = ±0,05 кH;
XD = –1,18 кH; YD = 0,05 кH; L = 0,71 кН∙м.
|
из
5.00
|
Обсуждение в статье: Равновесие тел под действием произвольной плоской системы сил |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

