 |
Главная |
Приведение произвольной системы сил к простейшему виду
|
из
5.00
|
Основная теорема статики.Произвольную систему сил, действующую на твердое тело, можно заменить эквивалентной системой, состоящей из силы и пары сил. Сила равна главному вектору системы сил и приложена в произвольно выбранной точке тела (центре приведения), момент пары равен главному моменту системы сил относительно этой точки.
Главный вектор системы сил  :
:

определяется своими проекциями на оси координат:
 ,
,  ,
,  ,
,
 .
.
Главный момент системы сил относительно центра O:

определяется своими проекциями на оси координат:
 ,
,  ,
,  ,
,
 .
.
Возможны следующие случаи приведения системы сил к центру:
1. 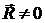 ,
,  .
.
Система сил приводится к равнодействующей. Линия действия равнодействующей проходит через центр приведения.
2.  ,
, 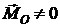 .
.
Система сил приводится к паре сил.
3. 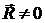 ,
, 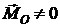 ,
,  − система сил имеет равнодействующую, которая не проходит через центр приведения. Ее линия действия определяется уравнениями
− система сил имеет равнодействующую, которая не проходит через центр приведения. Ее линия действия определяется уравнениями

4. 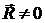 ,
, 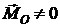 ,
,  − система сил приводится к динамическому винту (силе и паре, лежащей в плоскости, перпендикулярной силе).
− система сил приводится к динамическому винту (силе и паре, лежащей в плоскости, перпендикулярной силе).
Момент пары сил динамического винта
 .
.
Ось динамического винта определяется уравнениями
 .
.
 5.
5.  ,
,  − уравновешенная система сил.
− уравновешенная система сил.
Пример 1.4.1. Привести систему сил (рис. 1.4.1) к простейшему виду, если F1 = 5 Н, F2 = 15 Н, F3 = 10 Н, F4 = 3 Н, a = 2 м.
Решение:
1. За центр приведения выберем начало координат – точку O (рис. 1.4.2) и укажем углы a и b, определяющие положение силы  .
.
2. Найдем проекции главного вектора на оси координат:
 ,
,
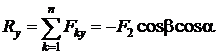 ,
,
 .
.
Откуда
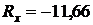 Н,
Н,  Н,
Н,  Н,
Н,
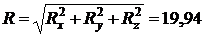 Н.
Н.
3. Вычислим проекции главного момента относительно точки О на оси координат:
 ,
,
 ,
,
 ,
,
Откуда
 Н·м,
Н·м, 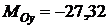 Н·м,
Н·м,  Н·м,
Н·м,
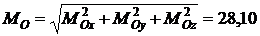 Н·м.
Н·м.
4. Найдем величину скалярного произведения главного вектора и главного момента
 .
.
Так как 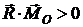 , то система сил приводится к правому динамическому винту. Вектор момента пары динамического винта и главный вектор совпадают по направлению.
, то система сил приводится к правому динамическому винту. Вектор момента пары динамического винта и главный вектор совпадают по направлению.
5. Уравнения оси динамического винта имеет вид:

или с учетом найденных значений:

или
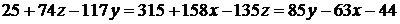 .
.
Для построения оси динамического винта найдем точки A и B ее пересечения с координатными плоскостями Oxy и Oyz, соответственно
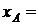 –1,703 м
–1,703 м 
 –0,203 м
–0,203 м  1,063 м
1,063 м

 1,995 м
1,995 м
 6. Определим момент пары сил динамического винта
6. Определим момент пары сил динамического винта
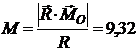 Н·м.
Н·м.
7. По координатам точек A и B изобразим ось динамического винта (рис. 1.4.3). В произвольной точке этой оси укажем силу, равную главному вектору  и вектор момента пары
и вектор момента пары  .
.
Задача 1.4.1. Имеет ли равнодействующую система сил, для которой главный вектор  и главный момент относительно центра О
и главный момент относительно центра О  .
.
Ответ: да.
Задача 1.4.2. Имеет ли равнодействующую система сил, для которой главный вектор 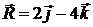 и главный момент относительно центра О
и главный момент относительно центра О 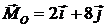 .
.
Ответ: нет.
 Задача 1.4.3. Определить расстояние от центра приведения О долинии действия равнодействующей системы сил (рис. 1.4.4), если ее главный вектор R = 15 Н и главный момент МО = 30 Н·м.
Задача 1.4.3. Определить расстояние от центра приведения О долинии действия равнодействующей системы сил (рис. 1.4.4), если ее главный вектор R = 15 Н и главный момент МО = 30 Н·м.
Ответ: 2 м.
Задача 1.4.4. Определить угол между главным вектором и главным моментом изображенной на рисунке 1.4.5 системы сил, принимая за центр приведения точку O, если F1 = F2 = 2 Н, момент пары сил M1 = 3 Н·м, OА = 1,5 м.
Ответ: α = 0º.
 Задача 1.4.5. Определить угол между главным вектором и главным моментом изображенной на рисунке 1.4.6 системы сил, принимая за центр приведения точку О, если F1 = F2 = F3 = 10 Н, a = 3 м.
Задача 1.4.5. Определить угол между главным вектором и главным моментом изображенной на рисунке 1.4.6 системы сил, принимая за центр приведения точку О, если F1 = F2 = F3 = 10 Н, a = 3 м.
Ответ: α = 135º.
Задача 1.4.6. Найти главный вектор и главный момент системы сил, изображенной на рисунке 1.4.7, если F1 = F2 = F3 = 7 Н, а ОА = ОВ = ОС = 2 м. За центр приведения принять точку О.
Ответ: R = 0, МО = 17,146 Н·м.

| 
|
| Рис. 1.4.6 | Рис. 1.4.7 |
Задача 1.4.7. Привести систему сил, приложенных к вершинам параллелепипеда (рис. 1.4.8), к простейшему виду, если F1 = 16 Н, F2 = 12 Н, F3 = 20 Н, a = с = 2,4 м, b=1,8 м.
Ответ: система сил приводится к паре сил с моментом М = 48 Н·м.
Задача 1.4.8. Привести систему сил, приложенных к вершинам куба (рис. 1.4.9), к простейшему виду, если F1 = 15 Н, F2 = 40 Н, F3 = 25 Н,
F4 = F5 = 20 Н, a = 1,5 м.
Ответ: система сил приводится к паре сил с моментом М = 63,65 Н·м.
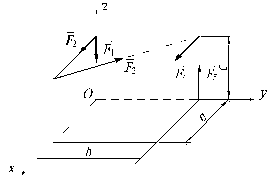
Задача 1.4.9. Привести систему сил, приложенных к правильной четырехугольной пирамиде, как показано на рис. 1.4.10, к простейшему виду, если F1 = F2 = F3 = F4 = 1 Н, F5 = 2,83 Н, АВ = AS = 2 м.
Ответ: система сил уравновешена.

| 
|
| Рис. 1.4.8 | Рис. 1.4.9 |

| 
|
| Рис. 1.4.10 | Рис. 1.4.11 |
Задача 1.4.10. Привести систему сил, приложенных к вершинам прямоугольного параллелепипеда (рис. 1.4.11), к простейшему виду, если F1 = F5 = 10 Н, F3 = 40 Н, F4 = 15 Н, F2 = 9 Н, a = 2,4 м, b = 3,2 м, c = 1 м.
Ответ: система сил приводится к равнодействующей R = 32 Н, линия действия которой параллельна оси Oy и проходит через точку А (0,9; 0; 0).
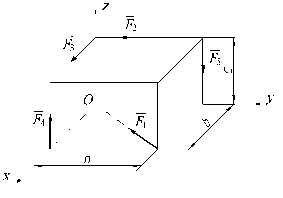
Задача 1.4.11. Привести систему сил, приложенных к вершинам прямоугольного параллелепипеда (рис. 1.4.12), к простейшему виду, если F1 = F3 = 3 Н, F2 = F6 = 6 Н, F4 = F5 = 9 Н, a = 3 м, b = 2 м, c = 1 м.
Ответ: система сил уравновешена.
Задача 1.4.12. Привести систему сил, приложенных к вершинам прямоугольного параллелепипеда (рис. 1.4.13), к простейшему виду, если F1 = F4 = F5 = 50 Н, F2 = 120 Н, F3 = 30 Н, a = 4 м, b = 3 м, c = 5 м.
Ответ: система приводится к равнодействующей R = 80 Н, линия действия которой параллельна оси Oy и проходит через точку А (0,0,10).
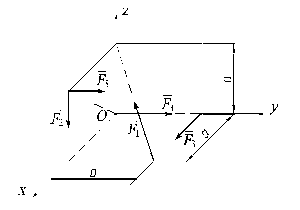
Задача 1.4.13. Привести систему сил, приложенных к вершинам куба (рис. 1.4.14), к простейшему виду, если a = 1 м, F1 = 866 Н, F2 = F3 = F4 = F5 = 500 Н. При решении принять  .
.
Ответ: система приводится к равнодействующей R = 7,07 Н.

| 
|
| Рис. 1.4.12 | Рис. 1.4.13 |
| 
|
| Рис. 1.4.14 | Рис. 1.4.15 |
Задача 1.4.14. Привести систему сил, приложенных к правильной треугольной пирамиде (рис. 1.4.15), к простейшему виду, если F1 = F2 = F3 = F4 = F5 = F6 = 1 Н, АВ = AS = 2 м.
 Ответ: система сил приводится к динамическому винту с R = 1,41 Н и М = 1,73 Н·м, ось силового винта проходит через вершину S перпендикулярно основанию пирамиды.
Ответ: система сил приводится к динамическому винту с R = 1,41 Н и М = 1,73 Н·м, ось силового винта проходит через вершину S перпендикулярно основанию пирамиды.
Задача 1.4.15. Вес радиомачты с основанием G = 140 кН. К мачте приложены сила натяжения антенны F = 20 кН и равнодействующая сил давления ветра P = 50 кН; обе силы горизонтальны и расположены во взаимно перпендикулярных плоскостях (рис. 1.4.16). Определить результирующую реакцию грунта, в котором уложено основание мачты.
Ответ: распределенная система сил реакции грунта приводится к левому динамическому винту с силой равной 150 кН и парой с моментом 60 кН∙м. уравнение центральной винтовой оси имеет вид
 .
.
Центр тяжести
Центром тяжести твердого тела называется центр параллельных сил тяжести  частиц данного тела.
частиц данного тела.
 ,
,
или



 Для определения положения центра тяжести однородных тел используют метод симметрии, метод разбиения на тела простой формы с известным положением центров тяжести, а также метод отрицательных масс (линий, площадей, объемов).
Для определения положения центра тяжести однородных тел используют метод симметрии, метод разбиения на тела простой формы с известным положением центров тяжести, а также метод отрицательных масс (линий, площадей, объемов).
Пример 1.5.1.Определить координаты центра тяжести плоской фермы (рис. 1.5.1), составленной из однородных стержней с одинаковым погонным весом.
Решение:
1. Применим метод разбиения, то есть представим ферму как совокупность семи стержней.
2. Найдем координаты центра тяжести фермы по формулам:
 ;
;  ,
,
где 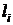 ,
,  ,
, 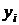 – длина и координаты центра тяжести стержня с номером
– длина и координаты центра тяжести стержня с номером  .
.
Длины и координаты центров тяжести стержней:



Тогда 
 ,
, 
Пример 1.5.2. Торцевая стена ангара (рис. 1.5.2) имеет форму полукруга 1 радиуса  с прямоугольным дверным проемом 2 высотой
с прямоугольным дверным проемом 2 высотой  и шириной
и шириной  Определить координаты центра тяжести стены.
Определить координаты центра тяжести стены.
Решение:
1. Применим методы симметрии и отрицательных площадей, рассматривая полукруг 1 и прямоугольный вырез 2.
2. Найдем координаты центра тяжести стены.
Поскольку ось Оy является осью симметрии, то координата 
Координату 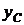 центра тяжести пластины определим по формуле
центра тяжести пластины определим по формуле

где  ,
,  ,
,  ,
,  – площади и координаты центров тяжести фигур 1 и 2.
– площади и координаты центров тяжести фигур 1 и 2.
Площади и координаты центров тяжести фигур:


Тогда

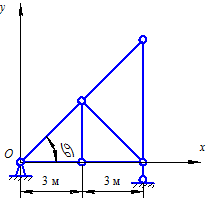
Задачи 1.5.1 – 1.5.4.Определить координаты центров тяжести плоских ферм (рис. 1.5.3 – 1.5.6), составленных из однородных стержней с одинаковым погонным весом.
Ответы к задачам 1.5.1 – 1.5.4:
| Номер задачи | 1.5.1 | 1.5.2 | 1.5.3 | 1.5.4 |
 , м , м
| 1,52 | 3,88 | 3,0 | 1,59 |
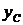 , м , м
| 0,69 | 1,96 | 1,73 | 0,17 |

| 
|
| Рис. 1.5.3 | Рис. 1.5.4 |

| 
|
| Рис. 1.5.5 | Рис. 1.5.6 |

| 
|
| Рис. 1.5.7 | Рис. 1.5.8 |
Задачи 1.5.5 – 1.5.7. Определить координаты центров тяжести однородных составных линий (рис. 1.5.7 – 1.5.9).
Ответы к задачам 1.5.5 – 1.5.7:
| Номер задачи | 1.5.5 | 1.5.6 | 1.5.7 |
 , см , см
| –4,76 | ||
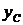 , см , см
| 14,16 | 3,31 |

| 
|
| Рис. 1.5.9 | Рис. 1.5.10 |

| 
|
| Рис. 1.5.11 | Рис. 1.5.12 |
Задача 1.5.8. Изогнутая под прямым углом однородная проволока подвешена на нити (рис. 1.5.10). Найти соотношение между длинами участков AD и AE, при котором участок AE находится в горизонтальном положении. АВ = 0,3 l1.
Ответ: 
Задача 1.5.9. Определить координаты центра тяжести однородной проволоки (рис. 1.5.11), если a = 3 м, b = 2 м, c = 1,5 м.
Ответ: xC = 1,69 м, yC = 1,38 м, zC = 1,33 м.
Задача 1.5.10. Однородный замкнутый контур, ограничивающий полукруг, подвешен на нити (рис. 1.5.12). Определить угол α между горизонталью и диаметром полуокружности.
Ответ: α = 68,74º.
Задачи 1.5.11 – 1.5.14.Определить координаты центров тяжести однородных плоских фигур (рис. 1.5.13 – 1.5.16).
Ответы к задачам 1.5.11 – 1.5.14:
| Номер задачи | 1.5.11 | 1.5.12 | 1.5.13 | 1.5.14 |

| 37,07 см | 32,38 см | 2,31 м | |
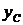
| 11,88 см | 24,83 см | 1,56 м |

| 
|
| Рис. 1.5.13 | Рис. 1.5.14 |

| 
|
| Рис. 1.5.15 | Рис. 1.5.16 |

| 
|
| Рис. 1.5.17 | Рис. 1.5.18 |
Задача 1.5.15. Подставка для цапфы подшипника представляет собой деталь, состоящую из опоры в виде параллелепипеда и шпонки в форме куба (рис. 1.5.17). Определить координаты центра тяжести подставки. Размеры указаны в миллиметрах.
Ответ:
Задача 1.5.16. Цапфа подшипника скольжения представляет собой деталь, состоящую из параллелепипеда и цилиндрической опоры (рис. 1.5.18). Определить координаты центра тяжести цапфы. Размеры указаны в миллиметрах.
Ответ: 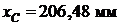 ,
,  ,
, 
Задача 1.5.17. Однородное тело, сечение которого изображено на рисунке 1.5.19, состоит из полушара, цилиндрической части и кругового конуса. Определить координаты центра тяжести тела. Размеры указаны в миллиметрах.
Ответ:  ,
, 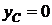 ,
, 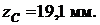
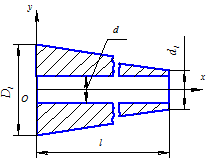
Задача 1.5.18. Ствол танковой пушки имеет форму усеченного конуса длины  (рис. 1.5.20). Наружный диаметр ствола в месте крепления к казенной части пушки
(рис. 1.5.20). Наружный диаметр ствола в месте крепления к казенной части пушки  наружный диаметр в сечении, соответствующем дульному срезу канала ствола,
наружный диаметр в сечении, соответствующем дульному срезу канала ствола,  Калибр пушки d =100 мм. Определить координату
Калибр пушки d =100 мм. Определить координату  центра тяжести ствола.
центра тяжести ствола.
Ответ: 
Задача 1.5.19. Определить координаты центра тяжести однородного тела, состоящего из двух прямоугольных параллелепипедов (рис. 1.5.21). В нижнем параллелепипеде сделан вырез в форме четверти цилиндра с радиусом основания R = 10 см. Размеры на рисунке указаны в см.
Ответ: xC = 17,1 см, yC = 20,99 см, zC = 7,84 см.
Задача 1.5.20. Определить координаты центра тяжести однородного тела (рис. 1.5.22), состоящего из треугольной призмы и параллелепипеда с вырезом. Размеры на рисунке указаны в см.

| 
|
| Рис. 1.5.19 | Рис. 1.5.20 |

| 
|
| Рис. 1.5.21 | Рис. 1.5.22 |
Ответ: xC = 20,14 см, yC = 35,14 см, zC = 5 см.
Часть 2. Кинематика
Кинематика точки
Существуют три аналитических способа задания движения точки: векторный, координатный и естественный.
При векторном способе радиус-вектор 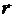 движущейся точки задается как функция времени
движущейся точки задается как функция времени  . Векторы скорости и ускорения точки равны соответственно первой и второй производной по времени от радиус-вектора:
. Векторы скорости и ускорения точки равны соответственно первой и второй производной по времени от радиус-вектора:
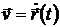 ,
,  .
.
Связь между радиус-вектором 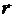 и декартовыми координатами точки выражается равенством:
и декартовыми координатами точки выражается равенством:  , где
, где  ,
,  ,
,  – орты осей координат.
– орты осей координат.
При координатном способе закон движения точки в декартовой системе координат дается заданием трех функций: 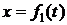 ,
,  ,
, 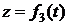 . Проекции скорости и ускорения на оси координат, а также модули скорости и ускорения точки определяются по формулам:
. Проекции скорости и ускорения на оси координат, а также модули скорости и ускорения точки определяются по формулам:
 ,
,  ,
, 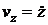 ,
,  ,
,
 .
.
При естественном способе задается траектория точки и закон движения точки по траектории  , где криволинейная координата
, где криволинейная координата  отсчитывается вдоль дуги от некоторой фиксированной точки на траектории. Алгебраическое значение скорости определяется по формуле
отсчитывается вдоль дуги от некоторой фиксированной точки на траектории. Алгебраическое значение скорости определяется по формуле  , а ускорение точки равно геометрической сумме касательного
, а ускорение точки равно геометрической сумме касательного  и нормального
и нормального  ускорений, т.е.
ускорений, т.е.  ,
,  ,
,  ,
,  ,
,  – радиус кривизны траектории в данной точке.
– радиус кривизны траектории в данной точке.
Пример 2.1.1. Снаряд движется в вертикальной плоскости согласно уравнениям  ,
,  (х ,у – в м, t – в с). Найти:
(х ,у – в м, t – в с). Найти:
– уравнение траектории;
– скорость и ускорение в начальный момент;
– высоту и дальность обстрела;
– радиус кривизны в начальной и в наивысшей точках траектории.
Решение:
1. Получим уравнения траектории снаряда, исключая параметр t из уравнений движения
 .
.
 Траектория снаряда – это участок параболы (рис. 2.1.1), имеющий ограничивающие точки: начальную с координатами х = 0, у = 0 и конечную, для которой х = L (дальность полета), у = 0.
Траектория снаряда – это участок параболы (рис. 2.1.1), имеющий ограничивающие точки: начальную с координатами х = 0, у = 0 и конечную, для которой х = L (дальность полета), у = 0.
2. Определим дальность полета снаряда, подставив у = 0 в уравнение траектории. Откуда найдем L = 24000 м.
3. Скорость и ускорение снаряда найдем по проекциям на оси координат:



В начальный момент времени v0 = 500 м/с, а = 10 м/с2.
4. Для определения высоты полета снаряда найдем время t1 полета до этой точки. В высшей точке проекция скорости на ось y равна нулю (рис. 2.1.1),  , откуда t1 = 40 с. Подставив t1 в выражение для координаты у, получим значение высоты Н = 8000 м.
, откуда t1 = 40 с. Подставив t1 в выражение для координаты у, получим значение высоты Н = 8000 м.
5. Радиус кривизны  траектории
траектории
 , где
, где  .
.
Откуда
 м;
м;  м.
м.
 Пример 2.1.2.В кривошипно-ползунном механизме (рис. 2.1.2) кривошип 1 вращается с постоянной угловой скоростью
Пример 2.1.2.В кривошипно-ползунном механизме (рис. 2.1.2) кривошип 1 вращается с постоянной угловой скоростью  рад/с. Найти уравнения движения, траекторию и скорость средней точки М шатуна 2, если ОА = АВ = 80 см.
рад/с. Найти уравнения движения, траекторию и скорость средней точки М шатуна 2, если ОА = АВ = 80 см.
Решение:
1. Запишем уравнения движения точки M в координатной форме (рис. 2.1.3)

2. Уравнение траектории получим, исключив время t из уравнения движения:

Траектория точки М – эллипс с центром в начале координат и полуосями 120 см и 40 см.
3. Скорость точки определим по проекциям на оси координат


Откуда

Задача 2.1.1.По заданным уравнениям движения точки найти уравнение ее траектории в координатной форме.
| Уравнение движения | Ответ |

| 
|

| 
|

| 
|

| 
|
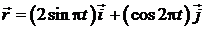
| 
|

| 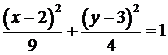
|
Задача 2.1.2. Найти уравнение траектории в координатной форме и закон движения точки по траектории, если даны уравнения ее движения в декартовых координатах. За начало отсчета дуговой координаты s принять начальное положение точки.
| Уравнение движения | Ответ |

|  , ,  ; ;
|
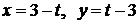
|  ; ; 
|

|  ; ; 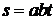
|

|  ; ; 
|
Задача 2.1.3. Движение точки задано уравнениями  ,
, 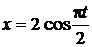 (
(  – в см,
– в см,  – в с). Найти уравнение траектории точки в координатной форме, скорость и ускорение, касательное и нормальное ускорения точки, а также радиус кривизны траектории в момент времени
– в с). Найти уравнение траектории точки в координатной форме, скорость и ускорение, касательное и нормальное ускорения точки, а также радиус кривизны траектории в момент времени  с. Изобразить траекторию точки и найденные векторы скорости и ускорений на чертеже.
с. Изобразить траекторию точки и найденные векторы скорости и ускорений на чертеже.
Ответ:  ; v1 = 3,56 см/с; a1 = 1,31 см/с2; aτ = 0,61 см/с2, an = 1,16 см/с2, ρ = 10,93 см.
; v1 = 3,56 см/с; a1 = 1,31 см/с2; aτ = 0,61 см/с2, an = 1,16 см/с2, ρ = 10,93 см.
Задача 2.1.4. Движение точки задано уравнениями  ,
,  (
(  – в см,
– в см,  – в с). Найти уравнение траектории точки, скорость и ускорение, касательное и нормальное ускорения точки в момент времени
– в с). Найти уравнение траектории точки, скорость и ускорение, касательное и нормальное ускорения точки в момент времени  . Найти радиус кривизны траектории. Изобразить траекторию точки и найденные векторы скорости и ускорений на чертеже.
. Найти радиус кривизны траектории. Изобразить траекторию точки и найденные векторы скорости и ускорений на чертеже.
Ответ:  ; v0 = 0; a0 = 7,2 см/с2; aτ = 7,2 см/с2, an = 0, ρ = ∞.
; v0 = 0; a0 = 7,2 см/с2; aτ = 7,2 см/с2, an = 0, ρ = ∞.
Задача 2.1.5. Движение точки задано уравнениями  ,
, 
(k и  – положительные постоянные величины). Найти уравнение траектории точки, скорость и ускорение, касательное и нормальное ускорения точки. Найти радиус кривизны траектории. Изобразить траекторию точки и векторы скорости и ускорений в момент времени
– положительные постоянные величины). Найти уравнение траектории точки, скорость и ускорение, касательное и нормальное ускорения точки. Найти радиус кривизны траектории. Изобразить траекторию точки и векторы скорости и ускорений в момент времени  на чертеже.
на чертеже.
Ответ:  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Задача 2.1.6. Движение точки задано уравнениями  ,
, 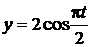 (
(  – в см,
– в см,  – в с). Найти уравнение траектории точки, скорость и ускорение, касательное и нормальное ускорения точки, а также радиус кривизны траектории в момент времени t1 = 1,5 с. Изобразить траекторию точки и найденные векторы скорости и ускорений на чертеже.
– в с). Найти уравнение траектории точки, скорость и ускорение, касательное и нормальное ускорения точки, а также радиус кривизны траектории в момент времени t1 = 1,5 с. Изобразить траекторию точки и найденные векторы скорости и ускорений на чертеже.
Ответ:  ; v1 = 3,85 см/с; a1 = 3,49 см/с2; aτ = 2,01 см/с2, an = 2,85 см/с2, ρ = 5,2 см.
; v1 = 3,85 см/с; a1 = 3,49 см/с2; aτ = 2,01 см/с2, an = 2,85 см/с2, ρ = 5,2 см.

|
| Рис. 2.1.4 |
Задача 2.1.7. Стержень (рис. 2.1.4) движется в плоскости  так, что его концы все время остаются на осях координат. Угол j, образуемый стержнем с осью
так, что его концы все время остаются на осях координат. Угол j, образуемый стержнем с осью  , меняется по закону
, меняется по закону  рад. Найти уравнения движения и траекторию точки
рад. Найти уравнения движения и траекторию точки  стержня, ее скорость, ускорение, касательное и нормальное ускорения, а также радиус кривизны траектории в момент времени, когда
стержня, ее скорость, ускорение, касательное и нормальное ускорения, а также радиус кривизны траектории в момент времени, когда  , если AB = 10 см, AD = 6 см.
, если AB = 10 см, AD = 6 см.
Ответ:  ;
;  ;
;  ; v1 = 9,42 см/с; a1 = 9,87 см/с2; aτ = 0, an = 9,87 см/с2, ρ = 9 см.
; v1 = 9,42 см/с; a1 = 9,87 см/с2; aτ = 0, an = 9,87 см/с2, ρ = 9 см.

|
| Рис. 2.1.5 |
Задача 2.1.8. Трубка 1 (рис. 2.1.5) вращается в плоскости Oxy с постоянной угловой скоростью ω. Шарик 2 скользит по трубке согласно закону  . Найти уравнения движения шарика в декартовых координатах, законы изменения его скорости и ускорения, а также радиус кривизны траектории шарика в той точке, которую шарик пройдет со скоростью u.
. Найти уравнения движения шарика в декартовых координатах, законы изменения его скорости и ускорения, а также радиус кривизны траектории шарика в той точке, которую шарик пройдет со скоростью u.
Ответ:  ,
,  ,
,  ,
,  ,
,  .
.
Задача 2.1.9.Точка движется по окружности радиуса 8 м по закону 
(  – длина дуги в м,
– длина дуги в м,  – время в с). Определить законы изменения скорости и ускорения точки.
– время в с). Определить законы изменения скорости и ускорения точки.
Ответ:  м/с,
м/с, 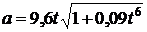 м/с2.
м/с2.
Задача 2.1.10.Точка, двигаясь равнозамедленно по окружности, за 0,5 с прошла путь 2 м, равный половине длины окружности. Определить скорость, ускорение, касательное и нормальное ускорения точки при t = 0,5 с, если ее начальная скорость равна 5 м/с.
Ответ: v = 3 м/с; a = 14,69 м/с2; aτ = 4 м/с2, an = 14,14 м/с2.
Задача 2.1.11.Точка движется по окружности радиуса 1,5 м. Когда угол между векторами скорости и ускорения точки составляет 60°, а модуль ускорения равен 7,5 м/с2. Определить скорость точки, касательное и нормальное ускорения в этот момент движения.
Ответ: v = 3,12 м/с; aτ = 3,75 м/с2, an = 6,5 м/с2.
Задача 2.1.12.Точка движется по некоторой траектории по закону 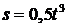
(  – длина дуги в м,
– длина дуги в м,  – время в с). Определить радиус кривизны траектории в положении, которое займет точка, спустя две секунды после начала движения, если в этот момент векторы скорости и ускорения точки составляют угол 30°.
– время в с). Определить радиус кривизны траектории в положении, которое займет точка, спустя две секунды после начала движения, если в этот момент векторы скорости и ускорения точки составляют угол 30°.
Ответ: 10,39 м.
Задача 2.1.13.Точка движется по дуге окружности радиуса R так, что центральный угол  , опирающийся на эту дугу, изменяется по закону
, опирающийся на эту дугу, изменяется по закону  . Найти для точки: 1) закон движения в естественной форме; 2) касательное и нормальное ускорения точки в те моменты времени, когда
. Найти для точки: 1) закон движения в естественной форме; 2) касательное и нормальное ускорения точки в те моменты времени, когда  и когда угол
и когда угол  наибольший.
наибольший.
Ответ: 1)  ; 2)
; 2)  ,
,  ,
,  ;
;  ,
, 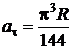 ,
,


