 |
Главная |
Представления конечных групп
|
из
5.00
|
Содержание
Основные обозначения
Введение
1. Представления конечных групп
Представления групп
Представления унитарными матрицами и полная приводимость представлений конечных групп
Лемма Шура
Соотношения ортогональности для характеров
Индуцированные представления
Произведение представлений
Заключение
Список использованных источников
Основные обозначения
 – группа – группа
|
 – порядок группы – порядок группы 
|
 – единичный элемент группы – единичный элемент группы 
|
 – единичная подгруппа, единичная группа – единичная подгруппа, единичная группа
|
 – множество всех простых делителей натурального числа – множество всех простых делителей натурального числа 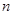
|
 – множество всех простых делителей порядка группы – множество всех простых делителей порядка группы 
|
 – центр группы – центр группы 
|
 – подгруппа Фиттинга группы – подгруппа Фиттинга группы 
|
 – подгруппа Фраттини группы – подгруппа Фраттини группы 
|
 – коммутант группы – коммутант группы 
|
 – централизатор подгруппы – централизатор подгруппы  в группе в группе 
|
 – нормализатор подгруппы – нормализатор подгруппы  в группе в группе 
|
 – группа всех автоморфизмов группы – группа всех автоморфизмов группы 
|
 – группа всех внутренних автоморфизмов группы – группа всех внутренних автоморфизмов группы 
|
 - -  является подгруппой группы является подгруппой группы 
|
 – –  является собственной подгруппой группы является собственной подгруппой группы 
|
 – –  является максимальной подгруппой группы является максимальной подгруппой группы 
|
 – –  является нормальной подгруппой является нормальной подгруппой 
|
 – –  является субнормальной подгруппой группы является субнормальной подгруппой группы 
|
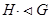 – –  является минимальной нормальной подгруппой группы является минимальной нормальной подгруппой группы 
|
 – индекс подгруппы – индекс подгруппы  в группе в группе 
|
 – прямое произведение подгрупп – прямое произведение подгрупп 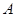 и и 
|
 – полупрямое произведение нормальной подгруппы – полупрямое произведение нормальной подгруппы 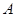 и подгруппы и подгруппы 
|
Введение
В данной работе приведены доказательства следующих теорем:
Теорема. Непустое подмножество  группы
группы  будет подгруппой тогда и только тогда, когда
будет подгруппой тогда и только тогда, когда  и
и  для всех
для всех  .
.
Группой называется непустое множество  с бинарной алгебраической операцией (умножением), которая удовлетворяет следующим требованием:
с бинарной алгебраической операцией (умножением), которая удовлетворяет следующим требованием:
1) операция определена на  , т.е.
, т.е.  для всех
для всех  ;
;
2) операция ассоциативна, т.е.  для любых
для любых  ;
;
3) в  существует единичный элемент, т.е. такой элемент
существует единичный элемент, т.е. такой элемент  , что
, что  для всех
для всех  , что
, что  для всех
для всех  ;
;
4) каждый элемент обладает обратным, т.е. для любого  существует такой элемент
существует такой элемент  , что
, что  .
.
Более кратко: полугруппа с единицей, в которой каждый элемент обладает обратным, называется группой.
Группу с коммутативной операцией называют коммутативной или абелевой. Если  – конечное множество, являющиеся группой, то
– конечное множество, являющиеся группой, то  называют конечной группой, а число
называют конечной группой, а число  элементов в
элементов в  – порядком группы
– порядком группы  .
.
Подмножество  группы
группы  называется подгруппой, если
называется подгруппой, если  – группа относительно той же операции, которая определена на
– группа относительно той же операции, которая определена на  . Запись
. Запись  означает, что
означает, что  – подгруппа группы
– подгруппа группы  , а
, а  – что
– что  – собственная подгруппа группы
– собственная подгруппа группы  , т.е.
, т.е.  и
и 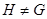 .
.
Централизатор. Пусть  – непустое подмножество группы
– непустое подмножество группы  . Совокупность всех элементов группы
. Совокупность всех элементов группы  , перестановочных с каждым элементом множества
, перестановочных с каждым элементом множества  , называется централизатором множества
, называется централизатором множества  в группе
в группе  и обозначается через
и обозначается через  .
.
Лемма
1. Если  – подмножество группы
– подмножество группы  , то централизатор
, то централизатор  является подгруппой.
является подгруппой.
2. Если  и
и  – подмножество группы
– подмножество группы  и
и  , то
, то 
3. Если  – подмножество группы
– подмножество группы  и
и  , то
, то 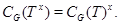
Центр группы. Центром группы  называется совокупность всех элементов из
называется совокупность всех элементов из  , перестановочных с каждым элементом группы. Центр обозначается через
, перестановочных с каждым элементом группы. Центр обозначается через  . Ясно, что
. Ясно, что  , т.е. центр группы
, т.е. центр группы  совпадает с централизатором подмножества
совпадает с централизатором подмножества  в группе
в группе  . Кроме того,
. Кроме того, 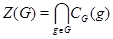 .
.
Зафиксируем в группе  элемент
элемент 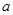 . Пересечение всех подгрупп группы
. Пересечение всех подгрупп группы  , содержащих элемент
, содержащих элемент 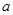 , назовем циклической подгруппой, порожденной элементом
, назовем циклической подгруппой, порожденной элементом  , и обозначим через
, и обозначим через 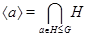 .
.
Теорема. Циклическая подгрупппа 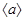 , порожденная элементом
, порожденная элементом 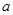 , состоит из всевозможных целых степеней элемента
, состоит из всевозможных целых степеней элемента 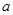 , т.е.
, т.е. 
Следствие. Циклическая подгруппа абелева.
Порядок элемента. Пусть 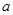 – элемент группы
– элемент группы  . Если все степени элемента
. Если все степени элемента  различны, т.е.
различны, т.е.  для всех целых
для всех целых  , то говорят, что элемента
, то говорят, что элемента 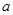 имеет бесконечный порядок.
имеет бесконечный порядок.
Нормализатор. Если  – непустое подмножество группы
– непустое подмножество группы  и
и  то
то  и
и  Элемент
Элемент  называется перестановочным с подмножеством
называется перестановочным с подмножеством  , если
, если 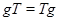 . Равенство
. Равенство 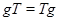 означает, что для любого элемента
означает, что для любого элемента  существует такой элемент
существует такой элемент  , что
, что 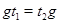 . Если элемент
. Если элемент  перестановочен с подмножеством
перестановочен с подмножеством  , то
, то 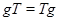 и
и  . Совокупность всех элементов группы
. Совокупность всех элементов группы  , перестановочных с подмножеством
, перестановочных с подмножеством  , называется нормализатором подмножества
, называется нормализатором подмножества  в группе
в группе 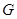 и обозначается через
и обозначается через  . Итак,
. Итак,

Лемма. Пусть 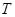 – непустое подмножество группы
– непустое подмножество группы  ,
,  – произвольный элемент группы
– произвольный элемент группы 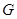 . Тогда:
. Тогда:
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5) если  – подгруппа группы
– подгруппа группы 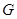 , то
, то 
Подгруппа  называется нормальной подгруппой группы
называется нормальной подгруппой группы  , если
, если  для всех
для всех  . Запись
. Запись  читается: »
читается: »  – нормальная подгруппа группы
– нормальная подгруппа группы  «. Равенство
«. Равенство  означает, что для любого элемента
означает, что для любого элемента  существует элемент
существует элемент  такой, что
такой, что 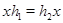 .
.
Теорема. Для подгруппы  группы
группы 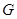 следующие утверждения эквивалентны:
следующие утверждения эквивалентны:
1)  – нормальная подгруппа;
– нормальная подгруппа;
2) подгруппа  вместе с каждым своим элементом содержит все ему сопряженные элементы, т.е.
вместе с каждым своим элементом содержит все ему сопряженные элементы, т.е.  для всех
для всех  ;
;
3) подгруппа  совпадает с каждой своей сопряженной подгруппой, т.е.
совпадает с каждой своей сопряженной подгруппой, т.е. 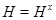 для всех
для всех  .
.
Лемма. Пусть  – подгруппа группы
– подгруппа группы 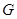 . Тогда:
. Тогда:
1)  ;
;
2) если  и
и 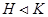 , то
, то  ;
;
3)  – наибольшая подгруппа группы
– наибольшая подгруппа группы 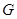 , в которой
, в которой  нормальна;
нормальна;
4) если 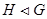 , то
, то  . Обратно, если
. Обратно, если  , то
, то 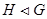 ;
;
5)  для любого непустого подмножества
для любого непустого подмножества 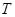 группы
группы  .
.
Простая группа. В каждой группе 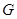 тривиальные подгруппы (единичная подгруппа
тривиальные подгруппы (единичная подгруппа  и сама группа
и сама группа 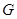 ) являются нормальными подгруппами. Если в неединичной группе
) являются нормальными подгруппами. Если в неединичной группе 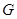 нет других нормальных подгрупп, то группа
нет других нормальных подгрупп, то группа  называется простой. Единичную группу
называется простой. Единичную группу  считают непростой.
считают непростой.
Представления конечных групп
Представления групп
Пусть  – группа всех невырожденных матриц порядка
– группа всех невырожденных матриц порядка 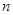 над полем
над полем  комплексных чисел. Если
комплексных чисел. Если 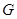 – произвольная группа, то ее (матричным) представлением называется любой ее гомоморфизм в
– произвольная группа, то ее (матричным) представлением называется любой ее гомоморфизм в 
 G
G  ,
,
такой, что
 ,
,
 (единичная матрица),
(единичная матрица),
 . Число n называется степенью этого представления. Если гомоморфизм A иньективен, то представление называется точным.
. Число n называется степенью этого представления. Если гомоморфизм A иньективен, то представление называется точным.
Пример 1.1 Отображение, переводящее каждый элемент группы  в
в  , является представлением степени
, является представлением степени  . Оно называется тождественным представлением группы
. Оно называется тождественным представлением группы 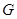 и обозначается через
и обозначается через  .
.
Пример 1.2 Если  – некоторое представление группы
– некоторое представление группы  , то для каждой невырожденной матрицы
, то для каждой невырожденной матрицы  отображение
отображение  также является представлением этой группы.
также является представлением этой группы.
Пусть  и
и  – два представления группы
– два представления группы  . Если существует невырожденная матрица
. Если существует невырожденная матрица  , такая, что что
, такая, что что
 ,
,
то представления  и
и 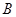 называются эквивалентными. Тот факт, что представления
называются эквивалентными. Тот факт, что представления  и
и 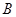 эквивалентны, мы будем обозначать так:
эквивалентны, мы будем обозначать так:  . Отношение
. Отношение  определяет классы эквивалентных представлений группы
определяет классы эквивалентных представлений группы 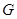 .
.
Пример 1.3. Пусть  – симметрическая группа степени
– симметрическая группа степени  . Для элемента
. Для элемента
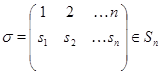
через 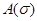 обозначим матрицу,
обозначим матрицу,  строка которой имеет вид
строка которой имеет вид  , где 1 стоит на
, где 1 стоит на 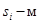 месте. Другими словами,
месте. Другими словами,

где

Такое отображение  является точным представлением группы
является точным представлением группы  .
.
1.4. Пусть  –конечная группа, состоящая из элементов
–конечная группа, состоящая из элементов  и пусть
и пусть  – симметрическая группа на
– симметрическая группа на  . Отображение, которое ставит в соответствие элементу
. Отображение, которое ставит в соответствие элементу 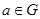 подстановку
подстановку
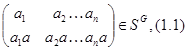
является инъективным гомоморфизмом группы  в
в  . С такой подстановкой
. С такой подстановкой  мы свяжем матрицу
мы свяжем матрицу

где, как и в примере  ,
,

Тогда отображение  является точным представлением группы
является точным представлением группы 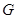 . Оно называется правым регулярным представлением этой группы. Определим
. Оно называется правым регулярным представлением этой группы. Определим 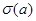 следующим образом:
следующим образом:

Тогда
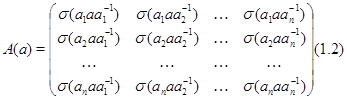
и, если  , то каждый диагональный элемент равен нулю.
, то каждый диагональный элемент равен нулю.
регулярное представление группы  определяется аналогично с использованием гомоморфизма
определяется аналогично с использованием гомоморфизма

Другими словами,

Пусть 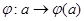 – некоторый гомоморфизм из
– некоторый гомоморфизм из  в
в  , т.е. подстановочное представление группы
, т.е. подстановочное представление группы  . Представив подстановку
. Представив подстановку  в виде матрицы
в виде матрицы  , как это сделано в примере 1.3, мы получим представление
, как это сделано в примере 1.3, мы получим представление 
Пусть  – представление степени
– представление степени  . Говорят, что
. Говорят, что 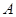 приводимо, если существует такая невырожденная матрица
приводимо, если существует такая невырожденная матрица 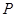 , что
, что

где  и
и  – квадратные матрицы порядка
– квадратные матрицы порядка  и
и  соответственно, причем
соответственно, причем  Отметим, что представления
Отметим, что представления


эквивалентны, поскольку  для матрицы
для матрицы

Скажем, что представление 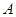 неприводимо, если оно не является приводимым. Отметим, что в (1.3) отображения
неприводимо, если оно не является приводимым. Отметим, что в (1.3) отображения  и
и  являются представлении степеней
являются представлении степеней  и
и  соответственно.
соответственно.
Для заданных представлений  и
и  группы
группы  степеней
степеней  и
и  соответственно отображение
соответственно отображение

является представление степени 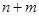 этой группы. Такое, представление называется прямой суммой представлений
этой группы. Такое, представление называется прямой суммой представлений 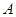 и
и  и обозначается через
и обозначается через  .
.
Представление 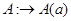 группы
группы 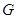 называется вполне приводимым, если оно эквивалентно прямой сумме некоторых неприводимых представлений, т.е. если найдется невырожденная матрица
называется вполне приводимым, если оно эквивалентно прямой сумме некоторых неприводимых представлений, т.е. если найдется невырожденная матрица 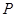 , такая, что
, такая, что

где каждое 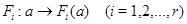 является неприводимым представлением группы
является неприводимым представлением группы 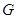 .
.
|
из
5.00
|
Обсуждение в статье: Представления конечных групп |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

