 |
Главная |
Соотношения ортогональности для характеров
|
из
5.00
|
Ниже везде предполагается, что рассматриваемые группы конечны.
Характеры. Для квадратной матрицы  порядка
порядка 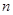 обозначим через
обозначим через  ее след, т.е.
ее след, т.е.

Путем прямых вычислений доказывается следующая
Лемма 4.1.

 для произвольной квадратной матрицы
для произвольной квадратной матрицы 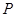 .
.
Для представления  группы
группы  положим
положим  Тогда
Тогда  – функция, принимающая значения в множестве
– функция, принимающая значения в множестве 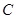 и называемая характером представления
и называемая характером представления 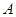 . Очевидно, что
. Очевидно, что  равно степени представления
равно степени представления 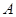 . Характеры неприводимых представлений называются неприводимыми характерами. Из леммы 4.1 (2) вытекает следующая
. Характеры неприводимых представлений называются неприводимыми характерами. Из леммы 4.1 (2) вытекает следующая
Лемма 4.2. Эквивалентные представления имеют один и тот же характер.
Поскольку  , имеет место равенство
, имеет место равенство  . Таким образом,
. Таким образом,  принимает одно и то же значение на всем классе сопряженных элементов группы
принимает одно и то же значение на всем классе сопряженных элементов группы  . Такие функции называются функциями классов.
. Такие функции называются функциями классов.
Первое соотношение ортогональности для характеров. Пусть  – группа порядка
– группа порядка  , а
, а  и
и  – ее неприводимые представления степеней
– ее неприводимые представления степеней 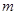 и
и 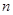 соответственно. Для произвольной
соответственно. Для произвольной 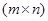 – матрицы
– матрицы  пусть
пусть

Тогда, положив  , получаем
, получаем

Поскольку  , как и
, как и  , пробегает группу
, пробегает группу  , то
, то

Предположим, что 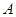 и
и  неэквивалентны. Тогда в силу леммы Шура
неэквивалентны. Тогда в силу леммы Шура  . Отсюда для
. Отсюда для  -го элемента матрицы
-го элемента матрицы 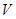 получаем
получаем

В частности, если взять  для некоторой пары
для некоторой пары 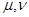 и
и  в остальных случаях, то
в остальных случаях, то

Пусть теперь  . Тогда в силу теоремы 3.2
. Тогда в силу теоремы 3.2 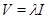 для некоторого
для некоторого 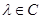 . При этом
. При этом  -ый элемент матрицы
-ый элемент матрицы 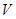 равен
равен

где  и
и  для
для  . Вычислив след матрицы
. Вычислив след матрицы

мы получаем  (здесь
(здесь 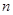 – степень представления
– степень представления 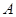 ), откуда
), откуда

Пусть  для некоторой пары
для некоторой пары 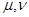 и
и  , если
, если 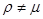 или
или  . Тогда
. Тогда
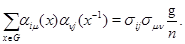
Тем самым мы получаем следующее утверждение.
Теорема 4.3. Пусть 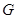 – группа порядка g.
– группа порядка g.
(1) Пусть  – неприводимое представление группы
– неприводимое представление группы 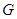 степени
степени 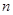 . Тогда
. Тогда
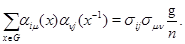
(2) Пусть  – неприводимое представление, не эквивалентное представлению
– неприводимое представление, не эквивалентное представлению  . Тогда
. Тогда

Пусть  – характеры представлений
– характеры представлений  и
и  . Положив в предыдущей теореме
. Положив в предыдущей теореме  и просуммировав по
и просуммировав по  , мы получаем теорему.
, мы получаем теорему.
Теорема 4.4. (Первое соотношение ортогональности для характеров.) Пусть  – группа порядка g.
– группа порядка g.
(1) Если  – неприводимый характер группы
– неприводимый характер группы 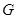 , то
, то

(2) Если  – характеры неэквивалентных неприводимых представлений группы
– характеры неэквивалентных неприводимых представлений группы 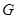 , то
, то

Отметим, что  для всех
для всех  , поскольку теорема 2.3 утверждает, что
, поскольку теорема 2.3 утверждает, что 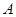 эквивалентно некоторому унитарному представлению
эквивалентно некоторому унитарному представлению  и потому
и потому

Пусть 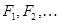 – представители классов эквивалентности неприводимых представлений группы
– представители классов эквивалентности неприводимых представлений группы 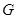 и
и  – характеры представлений
– характеры представлений 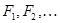 . Обозначим через
. Обозначим через  классы сопряженных элементов группы
классы сопряженных элементов группы 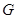 , причем
, причем 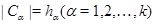 , и пусть
, и пусть  – представители этих классов. Поскольку характеры – это функции классов, теорема 4.4 может быть переписана в следующем виде.
– представители этих классов. Поскольку характеры – это функции классов, теорема 4.4 может быть переписана в следующем виде.
Теорема 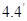 .
. 
Для функций  , определенных на группе
, определенных на группе 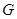 порядка
порядка  и принимающих значения в поле
и принимающих значения в поле  , определим скалярное произведение
, определим скалярное произведение  по следующему правилу:
по следующему правилу:

В случаях, когда ясно, о какой группе идет речь, мы иногда вместо  будем писать
будем писать  . Очевидно, что скалярное произведение является симметричной билинейной формой:
. Очевидно, что скалярное произведение является симметричной билинейной формой:

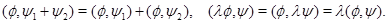
В этих обозначениях первое соотношение ортогональности для характеров можно сформулировать так:
Теорема  . Пусть
. Пусть  – характеры попарно неэквалентных неприводимых представлений группы
– характеры попарно неэквалентных неприводимых представлений группы 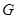 . Тогда
. Тогда 
Кратности неприводимых представлений. Пусть 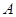 – некоторое представление группы
– некоторое представление группы 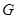 . Поскольку оно вполне приводимо в силу теоремы 2.3, оно эквивалентно представлению
. Поскольку оно вполне приводимо в силу теоремы 2.3, оно эквивалентно представлению
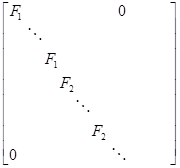
где  – неэквивалентные неприводимые представления. Число
– неэквивалентные неприводимые представления. Число  называется кратностью представления
называется кратностью представления 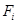 в
в  , и мы записываем
, и мы записываем

Пусть 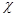 – характер представления
– характер представления 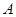 и
и  – характер представления
– характер представления  . Тогда
. Тогда

Если  , то
, то 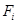 и
и  называют неприводимыми компонентами представления
называют неприводимыми компонентами представления 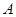 и характера
и характера 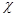 соответственно.
соответственно.
Теорема 4.5. Пусть 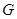 – группа и
– группа и 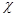 – характер некоторого ее представления. Пусть
– характер некоторого ее представления. Пусть  – кратность неприводимого характера
– кратность неприводимого характера  в
в 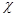 . Тогда
. Тогда

Доказательство. Пусть разложение 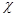 в сумму неприводимых характеров имеет вид
в сумму неприводимых характеров имеет вид 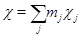 , где
, где  – кратность
– кратность  . Тогда
. Тогда
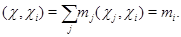
Теорема 4.6. Пусть 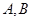 – представления группы
– представления группы 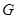 , а
, а  – их характеры. Тогда
– их характеры. Тогда 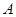 и
и  эквивалентны в том и только том случае, когда
эквивалентны в том и только том случае, когда 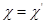 .
.
Доказательство. В силу предыдущей теоремы кратности компоненты  в
в 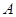 и
и 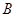 определяются характерами последних. Поскольку каждое представление группы
определяются характерами последних. Поскольку каждое представление группы 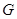 вполне приводимо, представления
вполне приводимо, представления 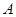 и
и  эквивалентны тогда и только тогда, когда каждое неприводимое представление
эквивалентны тогда и только тогда, когда каждое неприводимое представление 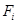 имеет в
имеет в 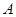 и
и  одну ту же кратность. Таким образом,
одну ту же кратность. Таким образом,  тогда и только тогда, когда
тогда и только тогда, когда  .
.
Пусть  – характер правого регулярного представления группы
– характер правого регулярного представления группы 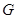 порядка
порядка  . Отметим, что
. Отметим, что

Для характера  произвольного неприводимого представления
произвольного неприводимого представления  выполняется соотношение
выполняется соотношение

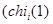 равно степени представления
равно степени представления 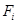 ). Следовательно, справедлива следующая
). Следовательно, справедлива следующая
Теорема 4.7. Пусть  – характер правого регулярного представления группы
– характер правого регулярного представления группы 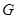 . Тогда каждое неприводимое представления
. Тогда каждое неприводимое представления 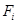 этой группы входит в
этой группы входит в  с кратностью
с кратностью  , где
, где  – степень представления
– степень представления 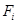 . Таким образом,
. Таким образом,

где суммирование ведется по всем неприводимым характерам 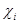 группы
группы  .
.
Заметим, что правое и левое регулярные представления эквивалентны, поскольку характер  левого регулярного представления также удовлетворяет равенству (4.8). Поэтому
левого регулярного представления также удовлетворяет равенству (4.8). Поэтому  .
.
Теорема 4.7 утверждает, что каждый неприводимый характер входит в  в качестве компоненты, и поэтому
в качестве компоненты, и поэтому 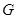 имеет лишь конечное число неприводимых характеров. Ниже мы покажем, что число неприводимых характеров группы
имеет лишь конечное число неприводимых характеров. Ниже мы покажем, что число неприводимых характеров группы 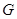 совпадает с числом ее классов сопряженных элементов.
совпадает с числом ее классов сопряженных элементов.
Теорема 4.8. Пусть  – полный набор различных неприводимых характеров группы
– полный набор различных неприводимых характеров группы 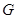 . Пусть
. Пусть  – степень
– степень  , а
, а 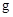 – порядок группы
– порядок группы 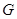 . Тогда
. Тогда

и

для  .
.
Для доказательства достаточно вычислить  на элементе
на элементе  , используя (4.8).
, используя (4.8).
Второе соотношение ортогональности для характеров. Пусть 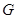 – группа, а
– группа, а 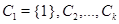 – ее классы сопряженных элементов. Образуем формальную сумму элементов из класса
– ее классы сопряженных элементов. Образуем формальную сумму элементов из класса  :
:

Определим произведение  и
и  по правилу
по правилу
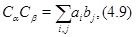
где  , а суммирование ведется по
, а суммирование ведется по  . Для элемента
. Для элемента  обозначим через
обозначим через  число пар
число пар  , таких, что
, таких, что  . Тогда для
. Тогда для  имеется в точности
имеется в точности  пар
пар  , таких, что
, таких, что  , поскольку
, поскольку  тогда и только тогда, когда
тогда и только тогда, когда  для
для  . Поэтому каждый элемент из
. Поэтому каждый элемент из  появляется в правой части равенства (4.9) одно и то же число раз, т.е.
появляется в правой части равенства (4.9) одно и то же число раз, т.е.

Совокупность всех элементов  для
для  также образует класс сопряженных элементов. Обозначим этот класс через
также образует класс сопряженных элементов. Обозначим этот класс через  .
.
Тогда

Пусть  – неприводимое представление группы
– неприводимое представление группы 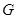 и
и  – степень
– степень  . Определим
. Определим  по правилу
по правилу

Тогда

поскольку  пробегает
пробегает  , как и
, как и  . Значит,
. Значит,  коммутируют с
коммутируют с  и в силу теоремы 3.2
и в силу теоремы 3.2

Взяв след от обеих частей равенства (4.12), мы получим

где 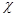 – характер представления
– характер представления  и
и  . В силу (4.10)
. В силу (4.10)

Подставив в это равенство (4.13), мы придем к равенству
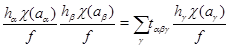
или

Пусть  – все различные неприводимые характеры группы
– все различные неприводимые характеры группы 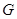 и
и 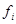 – степень
– степень  . Равенство (4.14) имеет место для каждого
. Равенство (4.14) имеет место для каждого  . Просуммировав (4.14) по
. Просуммировав (4.14) по  , получим
, получим



Отсюда

Величина  равна порядку централизатора
равна порядку централизатора 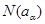 элемента
элемента  в группе
в группе 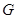 . Поскольку в силу (4.5)
. Поскольку в силу (4.5)  , мы получаем следующее утверждение.
, мы получаем следующее утверждение.
Теорема 4.9. (Второе соотношение ортогональности для характеров.) Пусть  – множество всех различных неприводимых характеров группы
– множество всех различных неприводимых характеров группы 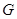 , и пусть
, и пусть  – полный набор представителей классов сопряженных элементов группы
– полный набор представителей классов сопряженных элементов группы 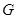 . Тогда
. Тогда

где 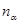 – порядок
– порядок  и суммирование ведется по всем неприводимым характерам
и суммирование ведется по всем неприводимым характерам  группы
группы 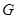 .
.
Теорема 4.10. Число различных неприводимых характеров группы  равно числу ее классов сопряженных элементов.
равно числу ее классов сопряженных элементов.
Доказательство. Мы воспользуемся следующим простым фактом, касающимся матриц. Пусть 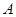 есть
есть  – матрица, а
– матрица, а  есть
есть 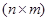 – матрица. Если определитель квадратной матрицы
– матрица. Если определитель квадратной матрицы  , имеющий порядок
, имеющий порядок  , отличен от нуля, то
, отличен от нуля, то  .
.
Пусть  – все различные неприводимые характеры группы
– все различные неприводимые характеры группы 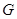 , а
, а  – полный набор представителей классов сопряженных элементов этой группы. Тогда по теореме
– полный набор представителей классов сопряженных элементов этой группы. Тогда по теореме 

Поэтому  . В силу теоремы 4.9
. В силу теоремы 4.9

Отсюда следует, что  и потому
и потому  .
.
|
из
5.00
|
Обсуждение в статье: Соотношения ортогональности для характеров |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

