 |
Главная |
Произведение представлений
|
из
5.00
|
Пусть  – квадратные матрицы порядков
– квадратные матрицы порядков 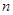 и
и 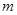 соответственно, и пусть
соответственно, и пусть 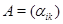 . Определим кронекерово, или тензорное, произведение
. Определим кронекерово, или тензорное, произведение 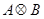 матриц
матриц 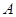 и
и 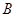 следующим образом:
следующим образом:
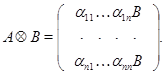
Значит, 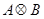 представляет собой квадратную матрицу порядка
представляет собой квадратную матрицу порядка 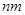 . Непосредственными вычислениями устанавливается следующая
. Непосредственными вычислениями устанавливается следующая
Лемма 6.1.
(1) 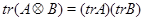 ,
,
(2) если 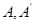 имеют степень
имеют степень 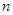 , a
, a 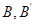 – степень
– степень 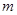 , то
, то 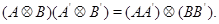
Пусть 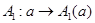 и
и 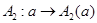 – представления группы
– представления группы 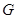 . Тогда в силу леммы 6.1 (2) отображение
. Тогда в силу леммы 6.1 (2) отображение
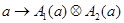
также является представлением этой группы. Такое представление называют произведением представлений 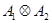 и обозначают через
и обозначают через 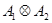 . Пусть
. Пусть 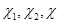 – характеры представлений
– характеры представлений 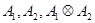 соответственно. По лемме 6.1 (1)
соответственно. По лемме 6.1 (1)
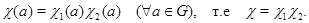
Пусть 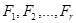 – полный набор неприводимых представлений группы
– полный набор неприводимых представлений группы 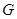 , а
, а 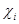 – характер
– характер 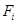 . Отображение
. Отображение 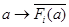 также является неприводимым, и его характер – это
также является неприводимым, и его характер – это 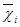 , где
, где 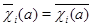 . Пусть
. Пусть 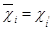 .
.
Теорема 6.2. Равенство
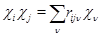
имеет место тогда и только тогда, когда
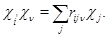
Доказательство.
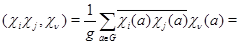
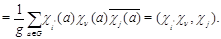
Таким образом, кратность вхождения 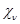 в
в 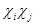 равна кратности вхождения
равна кратности вхождения 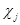 в
в 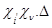
Теорема 6.3. Пусть 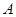 – точное представление группы
– точное представление группы 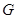 и
и 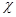 – его характер. Пусть
– его характер. Пусть 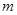 – число различных значений, которые принимает
– число различных значений, которые принимает 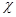 на
на 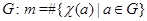 . Тогда каждое неприводимое представление группы
. Тогда каждое неприводимое представление группы 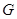 входит в
входит в
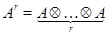
для некоторого 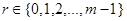 , где
, где 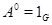 .
.
Доказательство. Предположим, что неприводимое представление 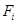 не входит в
не входит в 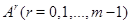 . Пусть
. Пусть 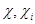 – характеры
– характеры 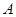 и
и 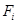 соответственно. Тогда
соответственно. Тогда
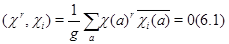
для 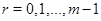 . Пусть
. Пусть 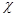 принимает на
принимает на 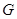 значение
значение 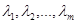 . Положим
. Положим 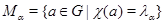 и
и 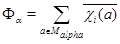 . В силу (6.1)
. В силу (6.1)
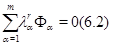
для 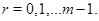 Рассмотрим (6.2) как систему линейных уравнений для
Рассмотрим (6.2) как систему линейных уравнений для 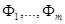 . Поскольку
. Поскольку 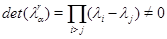 , эта система имеет решение
, эта система имеет решение 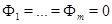 .
.
Пусть 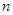 – степень представления
– степень представления 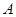 , т.е.
, т.е. 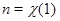 . Мы можем считать, что
. Мы можем считать, что 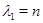 . Покажем, что
. Покажем, что 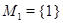 . Пусть
. Пусть 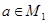 , т.е.
, т.е. 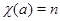 . Обозначим через
. Обозначим через 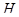 циклическую группу, порожденную элементом
циклическую группу, порожденную элементом 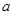 . По теореме 3.3
. По теореме 3.3 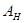 эквивалентно прямой сумме представлений степени 1. Значит, для некоторой невырожденной матрицы
эквивалентно прямой сумме представлений степени 1. Значит, для некоторой невырожденной матрицы 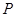
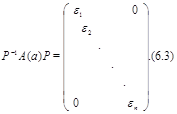
Пусть 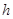 – порядок элемента
– порядок элемента 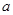 . Тогда
. Тогда 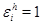 . Взяв след в равенстве (6.3), получаем
. Взяв след в равенстве (6.3), получаем 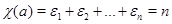 . Это означает, что
. Это означает, что 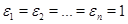 , т.е.
, т.е. 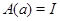 . Плскольку
. Плскольку 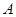 точно,
точно, 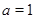 . Поэтому
. Поэтому 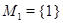 и
и 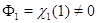 . Полученное противоречие доказывает теорему.
. Полученное противоречие доказывает теорему. 
Таблицы характеров. Пусть 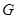 – группа и
– группа и 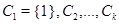 – классы сопряженных элементов в
– классы сопряженных элементов в 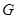 . Пусть
. Пусть 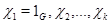 – нерпиводимые характеры группы
– нерпиводимые характеры группы 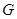 , а
, а 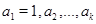 – представители ее классов сопряженных элементов. Отметим, что в силу теоремы 4.10 число неприводимых характеров совпадает с числом классов сопряженности. Упорядочим значения
– представители ее классов сопряженных элементов. Отметим, что в силу теоремы 4.10 число неприводимых характеров совпадает с числом классов сопряженности. Упорядочим значения 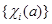 таким образом, чтобы получить таблицу характеров группы
таким образом, чтобы получить таблицу характеров группы 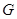 , в которой строки помечены различными неприводимыми характерами, начиная с
, в которой строки помечены различными неприводимыми характерами, начиная с 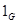 , а столбцы – классами сопряженности группы
, а столбцы – классами сопряженности группы 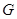 , начиная с класса
, начиная с класса 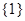 .
.
Различные строки таблицы характеров ортогональны между собой в смысле теоремы 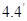 , а в силу теоремы 4.9 столбцы ортогональны между собой в обычном смысле как векторы комплексного унитарного пространства.
, а в силу теоремы 4.9 столбцы ортогональны между собой в обычном смысле как векторы комплексного унитарного пространства.
Заключение
Таким образом, в данной работе мы показали, что каждое представление конечной группы эквивалентно некоторому ее унитарному представлению и является мполне приводимым.
Путем прямых вычислений доказали лемму:
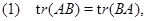
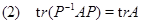 для произвольной квадратной матрицы
для произвольной квадратной матрицы 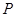 и теорему: Пусть
и теорему: Пусть 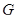 – группа и
– группа и 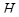 – ее подгруппа. Пусть
– ее подгруппа. Пусть 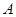 – представление
– представление 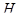 степени
степени 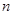 , а
, а 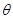 – его характер. Тогда индуцированное представление
– его характер. Тогда индуцированное представление 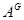 имеет степень
имеет степень 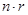 , где
, где 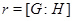 , и характер
, и характер
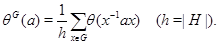
Непосредственными вычислениями была устанавлена следующая лемма: 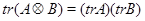 ,
,
(2) если 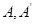 имеют степень
имеют степень 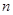 , a
, a 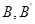 – степень
– степень  , то
, то 
Список использованных источников
Сыскин С.А. Абстрактные свойства простых спорадических групп. – Усп. мат. наук, 1980, т. 35, №5, (215), с. 181–212.
Монахов В.С. О трижды факторизуемых группах. – Изв. АН БССР. Сер. физ.-мат. наук, 1981, №6, с. 18–23.
Монахов В.С. Произведение разрешимой и циклической групп // Сб. VI всес. симпозиум по теории групп.-Киев: Наукова думка, 1980-с. 189–195
Монахов В.С. О произведении двух групп с циклическими подгруппами индекса 2 // Весцi АН Беларусi. сер. фiз.-мат. навук. – 1996, №3-с. 21–24
|
из
5.00
|
Обсуждение в статье: Произведение представлений |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

