 |
Главная |
Индуцированные представления
|
из
5.00
|
Пусть 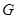 – группа и
– группа и  – ее подгруппа. Обозначим через
– ее подгруппа. Обозначим через 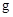 и
и 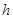 порядки групп
порядки групп 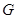 и
и  соответственно. Если
соответственно. Если  – некоторая функция на
– некоторая функция на 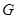 , то через
, то через  обозначим ее ограничение на
обозначим ее ограничение на  . В случае когда
. В случае когда  – функция классов на
– функция классов на  ,
,  также является функцией классов на
также является функцией классов на  . Если
. Если  – характер некоторого представления
– характер некоторого представления 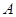 группы
группы 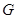 , то
, то  представляет собой характер ограничения
представляет собой характер ограничения  представления
представления 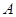 на
на  .
.
По функции  , заданной на
, заданной на  , определим функцию
, определим функцию  на
на 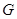 правилом
правилом

полагая  для
для 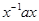 , не принадлежащих
, не принадлежащих  . Отметим, что
. Отметим, что  является функцией классов на
является функцией классов на 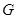 , даже еслм
, даже еслм  не является функцией классов на
не является функцией классов на  . Если
. Если  не сопряжен ни с каким элементом из
не сопряжен ни с каким элементом из  , то
, то  .
.
Лемма 5.1. Пусть  – функция классов на группе
– функция классов на группе 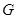 , а
, а  – функция классов на подгруппе
– функция классов на подгруппе  группы
группы 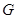 . Тогда
. Тогда

Доказательство. Имеем

Вклад в сумму дают лишь такие пары  , что
, что  . Поэтому, суммируя по тем парам
. Поэтому, суммируя по тем парам  , для которых
, для которых  при некотором
при некотором  , получаем
, получаем



Если  – характер некоторого представления группы
– характер некоторого представления группы  , то назовем
, то назовем  индуцированным характером группы
индуцированным характером группы  и скажем, что
и скажем, что  индуцирован с
индуцирован с  . Мы хотим показать, что каждый индуцированный характер действительно является характером некоторого представления группы
. Мы хотим показать, что каждый индуцированный характер действительно является характером некоторого представления группы 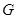 .
.
Пусть  – множество представителей левых смежных классов группы
– множество представителей левых смежных классов группы 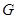 по
по  :
:

Для представления  подгруппы
подгруппы  определим матрицу
определим матрицу 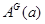 так:
так:
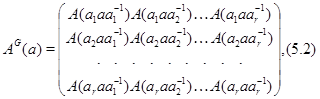
где для  , не содержащихся в
, не содержащихся в  , полагаем
, полагаем  . Это обобщение правого регулярного представления группы
. Это обобщение правого регулярного представления группы 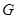 . Мы покажем, что
. Мы покажем, что

– представление группы 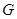 степени
степени  , где
, где  , а
, а  – степень
– степень 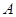 . При фиксированных
. При фиксированных  и
и  множество
множество  содержит по одному представителю из каждого левого смежного класса по
содержит по одному представителю из каждого левого смежного класса по  , поэтому среди матриц
, поэтому среди матриц  , лишь одна ненулевая. Аналогично, множество
, лишь одна ненулевая. Аналогично, множество  содержит по одному представителю из каждого правого смежного класса по
содержит по одному представителю из каждого правого смежного класса по  и среди матриц
и среди матриц 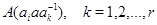 , также лишь одна ненулевая. Обозначим
, также лишь одна ненулевая. Обозначим 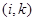 -й блок матрицы
-й блок матрицы  через
через  . Тогда
. Тогда

Покажем, что 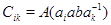 . Имеется единственное число
. Имеется единственное число  , такое, что
, такое, что 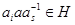 , и единственное число
, и единственное число  , такое, что
, такое, что  . Если
. Если  , то
, то  . Если же
. Если же 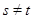 , то
, то 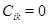 и
и  , поскольку
, поскольку  . В любом случае
. В любом случае  и следовательно,
и следовательно,  . Поскольку
. Поскольку  , матрица
, матрица  невырожденна. Таким образом
невырожденна. Таким образом 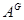 является представлением группы
является представлением группы 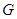 .
.
Пусть  – характер
– характер 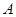 , а
, а 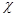 – характер
– характер 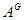 . Тогда
. Тогда


Тем самым мы получим  . Назовем
. Назовем  индуцированным представлением группы
индуцированным представлением группы 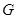 и будем говорить, что
и будем говорить, что  индуцировано с
индуцировано с 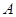 . Сказанное суммирует следующая
. Сказанное суммирует следующая
Теорема 5.2. Пусть 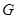 – группа и
– группа и  – ее подгруппа. Пусть
– ее подгруппа. Пусть 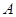 – представление
– представление  степени
степени 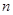 , а
, а  – его характер. Тогда индуцированное представление
– его характер. Тогда индуцированное представление 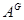 имеет степень
имеет степень  , где
, где  , и характер
, и характер
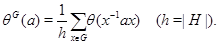
Теорема 5.3. (Закон взаимности Фробениуса.) Пусть  – подгруппа в
– подгруппа в 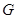 . Пусть
. Пусть  – полный набор неприводимых характеров группы
– полный набор неприводимых характеров группы  , а
, а 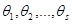 – полный набор неприводимых характеров группы
– полный набор неприводимых характеров группы  . Тогда
. Тогда

в том и только том случае, когда
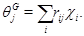
Другими словами, если 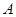 – неприводимое представление группы
– неприводимое представление группы  , а
, а 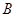 – неприводимое представление
– неприводимое представление  , то
, то  является неприводимой компонентой в
является неприводимой компонентой в  кратности
кратности  тогда и только тогда, когда
тогда и только тогда, когда 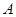 является неприводимой компонентой в
является неприводимой компонентой в  кратности
кратности 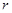 .
.
Доказательство. Пусть  и
и  . В силу леммы 5.1
. В силу леммы 5.1

|
из
5.00
|
Обсуждение в статье: Индуцированные представления |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

