Теоретические основы построения и анализа уравнения множественной регрессии

Множественной линейной регрессией называется выраженная в виде прямой зависимость среднего значения величины Y от двух или более других величин X1, X2, ..., Xm. Величину Y принято называть зависимой или результирующей переменной, а величины X1, X2, ..., Xm – независимыми или объясняющими переменными.

Множественная регрессия применяется в ситуациях, когда из множества факторов, влияющих на результативный признак, нельзя выделить один доминирующий фактор и необходимо учитывать влияние нескольких факторов.

Аналогично алгоритму построения парной регрессии, построение уравнения множественной регрессии состоит из спецификация модели и оценки параметров выбранной модели. Спецификация модели, в свою очередь, подразумевает отбор p факторов x_j, наиболее влияющих на величину y, а также выбор вида уравнения регрессии ŷ=f (x₁,x₂,...,x_р).

Отбор факторов в уравнение множетсвенной регрессии производится в первую очередь – исходя из сущности проблемы, во вторую очередь – на основе матрицы показателей корреляции определяют t-статистики для параметров регрессии. Коэффициенты корреляции между объясняющими переменными позволяют исключать из модели дублирующие факторы. Считается, что две переменные явно коллинеарные, т. е. находятся между собой в линейной зависимости, если r_x(i)x(j) ≥ 7,0. Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. В этом требовании проявляется специфика множественной регрессии как метода исследования комплексного воздействия факторов в условиях их независимости друг от друга.

После построения уравнения множественной регрессии производится её анализ. Одним из инструментов для анализа уравнения множественной регрессии является метод наименьших квадратов. Для линейных уравнений регрессии (и нелинейных уравнений, приводимых к линейным) строится система нормальных уравнений, решение которой позволяет получить оценки параметров регрессии. В случае линейной множественной регрессии система нормальных уравнений, принимает следующий вид, который представлен в формуле (1.13):

Для определения значимости факторов и повышения точности результата используется уравнение множественной регрессии в стандартизованном масштабе, составляемое по формуле (1.14):

где 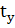, ,  – стандартизированные переменные;

        , ,  – стандартизированные коэффициенты регрессии.

Стандартизированные переменные находятся по формулам (1.16) и (1.17):

На основе полученного уравнения множественной регрессии в стандартизированном виде также проводится анализ с помощью метода наименьших квадратов. Стандартизованные коэффициенты регрессии показывают, на сколько сигм (средних квадратических отклонений) изменится в среднем результат, если соответствующий фактор х_i изменится на одну сигму при неизменном среднем уровне других факторов. В силу того, что все переменные заданы как центрированные и нормированные, стандартизованные коэффициенты регрессии β_i сравнимы между собой. На основе этого можно проводить ранжировку факторов по силе их воздействия на результатативный признак.

Помимо этого, в линейной модели множественной регрессии если факторные признаки различны по своей сущности или имеют различные единицы измерения, коэффициенты регрессии b_j являются несопоставимыми. Поэтому уравнение регрессии дополняют соизмеримыми показателями тесноты связи фактора с результатом, позволяющими ранжировать факторы по силе влияния на результат. К таким показателям относятся частные коэффициенты эластичности, представленные в формуле (1.11)

Данный коэффициент показывает, на сколько процентов в среднем по совокупности изменится результат у от своей величины при изменении фактора х на 1 % от своего значения при неизменных значениях других факторов.

Далее проводится анализ практической значимости уравнения множественной регрессии с помощью показателя множественной корреляции и коэффициента детерминации. Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком, или, иначе, оценивает тесноту совместного влияния факторов на результат и находится на формуле (1.12):

  где 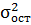 – остаточная дисперсия для уравнения ;

 – общая дисперсия результативного признака.

Показатель множественной корреляции может варьироваться от 0 до 1. Чем ближе его значение k 1, тем теснее связь результативного признака со всем набором исследуемых факторов.

    Коэффициент множественный детерминации находится как квадрат множественного коэффициента корреляции (индекс множественной корреляции). Коэффициент множественной детерминации показывает долю вариации результативного признака влияющих на него факторов. Величина коэффициента множественной детерминации используется для оценки качества регрессионной модели.

После расчета данных коэффициентов осуществяется проверка на гетероскедастичность, то есть, неоднородность наблюдений, выражающуюся в неодинаковой (непостоянной) дисперсии случайной ошибки регрессионной (эконометрической) модели. Гетероскедастичность противоположна гомоскедастичности, означающей однородность наблюдений, то есть постоянство дисперсии случайных ошибок модели.

Наличие гетероскедастичности случайных ошибок приводит к неэффективности оценок, полученных с помощьюметода наименьших квадратов. Кроме того, в этом случае оказывается смещённой и несостоятельной классическая оценка ковариационной матрицы МНК-оценок параметров. Следовательно статистические выводы о качестве полученных оценок могут быть неадекватными. В связи с этим тестирование моделей на гетероскедастичность является одной из необходимых процедур при построении регрессионных моделей.

В первом приближении наличие гетероскедастичности можно заметить на графиках остатков регрессии (или их квадратов) по некоторым переменным, по оцененной зависимой переменной или по номеру наблюдения. На этих графиках разброс точек может меняться в зависимости от значения этих переменных.

Для более строгой проверки применяют, например, статистические тесты Уайта, Голдфелда – Куандта, Бройша – Пагана, Парка, Глейзера, Спирмена.

В качестве примера можно рассмотреть тест Уайта, заключающийся в оценке определенной функции с помощью соответствующего уравнения регрессии для квадратов остатков, производимой по формуле (1.13):

где 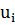 – случайный член.

Для нахождения расчетного значения Уайта необходимо сначала построить вспомогательное уравнение регрессии. Построение данного уравнения к исходной модели применяется МНК, затем находятся остатки регрессии, осуществляется регрессия квадратов этих остатков на все регрессоры, осуществляется регрессия квадратов этих остатков на квадраты регрессоров, а также регрессия квадратов этих остатков на попарные произведения регрессоров.

После построения вспомогательной регрессии, находится множественный коэффициент детерминации. Далее с помощью коэффициента детерминации вспомогательной регрессии по формуле (1.14) находится расчетное значение Уайта:

  где  – расчетное значение Уайта;

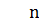 – кол-во наблюдений;

 – Множественный коэффициент детерминации.

После этого находится критическое значение показателя, которое сравнивается с расчётным значением Уайта. Если расчетное значение Уайта больше, то нулевая гипотеза отклоняется, т.е., с вероятностью  можно утверждать о наличие гетероскедастичности, и необходимо провести операции по устранению гетероскедастичности. Если расчетное значение Уайта меньше, то нулевая гипотеза принимается, т.е., с вероятностью  можно утверждать о наличие гомоскедастичности.

Поскольку МНК-оценки параметров моделей остаются несмещёнными состоятельными даже при гетероскедастичности, то при достаточном количестве наблюдений возможно применение обычного МНК. Однако, для более точных и правильных статистических выводов необходимо использовать стандартные ошибки в форме Уайта.

Таким образом, в этом методе каждое наблюдение взвешивается обратно пропорционально предполагаемому стандартному отклонению случайной ошибки в этом наблюдении. Такой подход позволяет сделать случайные ошибки модели гомоскедастичными. В частности, если предполагается, что стандартное отклонение ошибок пропорционально некоторой переменной Z, то данные делятся на эту переменную. Замена исходных данных их производными, например, логарифмом, относительным изменением или другой нелинейной функцией. Этот подход часто используется в случае увеличения дисперсии ошибки с ростом значения независимой переменной и приводит к стабилизации дисперсии в более широком диапазоне входных данных.