Определение коэффициентов уравнения регрессии методом Брандона

По этому методу уравнение регрессии записывается в виде:

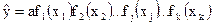,                               (5)

где  – любая функция величины .

Порядок расположения факторов 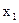, , …,  в выражении (5) следующий: чем больше влияние на у оказывает параметр , тем меньше должен быть порядковый номер j. Вид функции выбирается с помощью графических построений. Вначале по точкам выборки системы величин  строятся поле корреляции и эмпирическая линия регрессии . Таким образом, определяется тип зависимости

и методом наименьших квадратов рассчитываются коэффициенты этого уравнения регрессии. Затем составляется выборка новой величины

.

Эта величина уже не зависит от 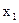, а определяется только параметрами , , …,  

.

По точкам новой выборки величин  и  вновь строятся корреляционное поле и эмпирическая линя регрессии, характеризующая зависимость  от :

.

Рассчитываются ее коэффициенты и вновь составляется выборка новой величины

.

Эта величина не зависит от двух факторов 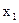 и  и может быть определена из следующего уравнения регрессии:

.

Такая процедура определения функций продолжается до получения выборки величины:

Эта величина не зависит от всех факторов 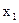, , …,  и определяется коэффициентом исходного уравнения:

где N – объем выборки.

Решение задачи планирования и нахождение уравнения регрессии. Полный факторный эксперимент

Методы планирования экспериментов позволяют свести к минимуму число необходимых опытов и одновременно выявить оптимальное значение искомой функции.

Оптимальный двухуровневый план (план 2^к). При планировании экспериментов условия опытов представляют собой фиксированное число значений уровней для каждого фактора. Если эксперименты проводятся только на двух уровнях (при двух значениях факторов) и при этом в процессе эксперимента осуществляются все возможные комбинации из k факторов, то постановка опытов по такому плану называется полным факторным экспериментом (ПФЭ) или планом 2 ^k.

Уровни факторов представляют собой в этом случае границы исследуемой области по данному технологическому параметру. Пусть, например, изучается влияние на выход продукта у трех факторов: температуры Т в диапазоне 100 – 200 ºС, давления Р в диапазоне 2 – 6 МПа (20 – 60 кгс/см²) и времени пребывания t в диапазоне 10 – 30 мин. Верхний уровень по температуре °С, нижний °С, 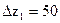 °С,  °С:

, .

Для произвольного i-го фактора:

, , .            (6)

Точка с координатами  носит название центра плана, иногда ее называют основным уровнем;  – единица варьирования (интервал варьирования) по оси . От системы координат , ,...,  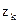перейдем к новой безразмерной системе координат , ,..., . Формула перехода (кодирования):

, .                                             (7)

Таблица 3. 3

№ опыта	Значение факторов в натуральном масштабе			Значение факторов в безраз-мерной системе координат			Выход
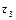
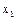
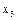
							y
1	100	20	10	-1	-1	-1	2
2	200	20	10	+1	-1	-1	6
3	100	60	10	-1	+1	-1	4
4	200	60	10	+1	+1	-1	8
5	100	20	30	-1	-1	+1	10
6	200	20	30	+1	-1	+1	18
7	100	60	30	-1	+1	+1	8
8	200	60	30	+1	+1	+1	12

В безразмерной системе координат верхний уровень равен +1 нижний равен –1, координаты центра плана равны нулю и совпадают с началом координат. В нашей задаче . Число возможных комбинаций N из трех факторов на двух уровнях равно . Запишем план проведения экспериментов (матрицу планирования) (табл. 3.3).

Значения выхода у, полученные в результате реализации плана экспериментов, приведены в последнем столбце таблицы.

Запишем кодированную матрицу планирования 2³ и результаты эксперимента, введя столбец так называемой фиктивной переменной  (табл. 3.4).

Таблица 3. 4

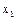
№ опыта					y
1	+1	-1	-1	-1	y1
2	+1	+1	-1	-1	y2
3	+1	-1	+1	-1	y3
4	+1	+1	+1	-1	y4
5	+1	-1	-1	+1	y5
6	+1	+1	-1	+1	y6
7	+1	-1	+1	+1	y7
8	+1	+1	+1	+1	y8

Приведенная в табл. 3.4 матрица планирования обладает следующими свойствами:

1) , , ;

2) , ;

3) ,

где k – число независимых факторов; N – число опытов в матрице планирования.

Первое свойство – равенство нулю скалярных произведений всех вектор-столбцов – свойство ортогональности матрицы планирования. Благодаря этому свойству резко уменьшаются трудности, связанные с расчетом коэффициентов уравнения регрессии, т.к. матрица коэффициентов нормальных уравнений  становится диагональной и ее диагональные элементы равны числу опытов в матрице планирования N. Диагональные элементы обратной матрицы :

.

Следовательно, любой коэффициент уравнения регрессии  определяется скалярным произведением столбца у на соответствующий столбец , деленным на число опытов N:

.                                                               (8)

Пользуясь планом, представленным в табл. 3.4, можно вычислить коэффициенты регрессии линейного уравнения

.                                              

Таблица 3.5

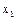
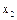
№ опыта									y
1	+1	-1	-1	-1	+1	+1	+1	-1	2
2	+1	+1	-1	-1	-1	-1	+1	+1	6
3	+1	-1	+1	-1	+1	+1	+1	+1	4
4	+1	+1	+1	-1	+1	-1	-1	-1	8
5	+1	-1	-1	+1	+1	-1	-1	+1	10
6	+1	+1	-1	+1	-1	+1	+1	-1	18
7	+1	-1	+1	+1	-1	-1	+1	-1	8
8	+1	+1	+1	+1	+1	+1	+1	+1	12

Если в рассмотрение ввести более полное уравнение регрессии с коэффициентами взаимодействия:

,

то для определения коэффициентов , ,  (эффектов двойного взаимодействия) и 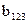 (тройного взаимодействия) необходимо расширить матрицу следующим образом (табл. 3.5).

Если поставить дополнительно параллельные опыты, можно определить , проверить значимость коэффициентов регрессии и при наличии степеней свободы – адекватность уравнения.

В связи с тем, что корреляционная матрица  для спланированного эксперимента есть матрица диагональная

коэффициенты уравнения регрессии некоррелированы между собой. Значимость коэффициентов можно проверить по критерию Стьюдента. Исключение из уравнения регрессии незначимого коэффициента не скажется на значениях остальных коэффициентов. При этом выборочные коэффициенты  оказываются так называемыми несмешанными оценками для соответствующих генеральных коэффициентов :

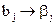
т.е. коэффициенты уравнения регрессии характеризуют вклад каждого фактора в величину у.

Диагональные элементы корреляционной матрицы равны между собой, поэтому все коэффициенты уравнений определяются с одинаковой точностью:

.

Дробные реплики

Если при получении уравнения можно ограничиться линейным приближением, то число опытов резко сокращается при использовании так называемых дробных реплик от полного факторного эксперимента или дробного факторного эксперимента (ДФЭ). Для того чтобы дробная реплика представляла собой ортогональный план, в качестве реплики следует брать ближайший полный факторный эксперимент. Число опытов при этом должно быть больше, чем число неизвестных коэффициентов в уравнении регрессии. Допустим, что нам нужно получить линейное приближение некоторого небольшого участка поверхности отклика при трех независимых факторах:

.

Для решения этой задачи можно ограничиться четырьмя опытами, если в планировании для ПФЭ 2² использовать столбец  (табл. 3.6) в качестве плана для  (табл. 3.7).

Таблица 3. 6

№ опыта
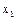
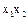
1	+1	+1	+1	+1
2	+1	-1	-1	+1
3	+1	-1	+1	-1
4	+1	+1	-1	-1

Таблица 3. 7

№ опыта
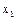
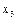
1	+1	+1	+1	+1
2	+1	-1	-1	+1
3	+1	-1	+1	-1
4	+1	+1	-1	-1

Такой сокращенный план – половина ПФЭ 2³ – носит название полуреплики от ПФЭ2³. Пользуясь таким планированием, можно оценить свободный член и три коэффициента уравнения регрессии при линейных членах.

На практике обычно не удается априори постулировать равенство нулю эффектов взаимодействия, однако часто имеются основания полагать, что некоторые из них малы по сравнению с линейными эффектами. Если коэффициенты регрессии при парных произведениях не равны нулю, то найденные нами коэффициенты будут смешанными оценками для генеральных коэффициентов:

, , ,

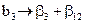где β – математические ожидания для соответствующих коэффициентов.

Эти генеральные коэффициенты не могут быть раздельно оценены по плану, включающему всего четыре опыта, так как в этом случае неразличимы столбцы для линейных членов и парных произведений. Если, например, в дополнение к столбцам, приведенным в таблице, мы вычисляем еще столбец для произведения , то увидим, что элементы этого столбца в точности равны элементам столбца . Таким образом, сокращение числа опытов приводит к получению смешанных оценок для коэффициентов. Для того чтобы определить, какие генеральные коэффициенты смешаны, удобно пользоваться таким приемом: поставив 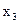 на место , получаем соотношение

,

называемое генерирующим соотношением. Умножив обе части соотношения на , справа получим единичный столбец

.

Произведение носит название определяющего контраста, с его помощью удобно определять, в каких столбцах одинаковые элементы.

Умножив по очереди определяющий контраст на , ,   находим:

, , . 

Полученным соотношениям соответствует система смешанных оценок.

При использовании ДФЭ необходимо иметь четкое представление о так называемой разрешающей способности дробной реплики, т. е. определить заранее, какие коэффициенты являются несмешанными оценками для соответствующих генеральных коэффициентов. Тогда в зависимости от поставленной задачи подбирается дробная реплика, с помощью которой можно извлечь максимальную информацию из эксперимента.

Например, в задаче с четырьмя факторами 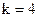, в качестве генерирующего соотношения можно взять

,                                                                 (9)

и любой из эффектов двойного взаимодействия, например

.                                                                      (10)

Матрица планирования с генерирующим соотношением (9) приведена в табл. 3.8.

Таблица 3. 8

№ опыта
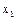
1	+1	+1	+1	+1	+1
2	+1	-1	-1	+1	+1
3	+1	-1	+1	+1	-1
4	+1	+1	-1	+1	-1
5	+1	+1	+1	-1	-1
6	+1	-1	-1	-1	-1
7	+1	-1	+1	-1	+1
8	+1	+1	-1	-1	+1

Воспользовавшись определяющим контрастом , при этом получаем систему совместных оценок:

, ;

, ;

, ;

, ;

, ;

, ;

, .

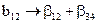В реальных задачах тройные взаимодействия бывают равными нулю значительно чаще, чем двойные. Значит, если нас более всего по физическому смыслу задачи интересуют оценки для линейных эффектов, следует брать генерирующее соотношение (9).

При генерирующем соотношении (10) матрица планирования имеет вид (табл. 3.9).

Таблица 3.9

№ опыта
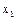
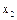
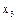
1	+1	+1	+1	+1	+1
2	+1	-1	-1	+1	+1
3	+1	-1	+1	+1	-1
4	+1	+1	-1	+1	-1
5	+1	+1	+1	-1	+1
6	+1	-1	-1	-1	+1
7	+1	-1	+1	-1	-1
8	+1	+1	-1	-1	-1

Определяющий контраст выражается соотношением . Получается следующая система оценок:

, ;

, ;

, ;

, ;

, ;

, ;

, .

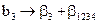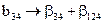Следовательно, дробную реплику с генерирующим соотношением (10), имеет смысл использовать, если нас более всего интересуют коэффициенты , , . Применяют дробные реплики и большей степени дробности (1/4 реплики, 1/8 реплики и т. п.).

Таким образом, оптимальные двухуровневые планы имеют следующие преимущества: планы ортогональны и поэтому все вычисления просты; все коэффициенты определяются независимо друг от друга: каждый коэффициент определяется по результатам всех N опытов; все коэффициенты регрессии определяются с одинаковой и минимальной дисперсией.

Композиционные планы

Полный факторный эксперимент  содержит слишком большое число опытов.

Сократить число опытов можно, если воспользоваться так называемыми композиционными, или последовательными планами, предложенными Боксом и Уилсоном. “Ядро” таких планов составляет ПФЭ  при  или дробная реплика от него при . Если линейное уравнение регрессии оказалось неадекватным, необходимо:

1) добавить 2k “звездных” точек, расположенных на координатных осях факторного пространства , , ..., , где  – расстояние от центра плана до “звездной” точки – “звездное” плечо;

2) увеличить число экспериментов в центре плана . Общее число опытов в матрице композиционного плана при k факторах составит:

, ;

, .

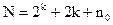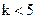Рассмотрим построение композиционных планов на примере  (рис. 3.2).

Рис. 3.2. Построение композиционного плана при k = 2

Точки 1, 2, 3, 4 образуют ПФЭ ; точки 5, 6, 7, 8 – “звездные” точки с координатами  и , координаты опытов в центре плана нулевые (0,0).

Величина звездного плеча  и количество опытов в центре плана  зависят от выбранного плана.

Ортогональные планы второго порядка

Композиционные планы легко приводятся к ортогональным выбором звездного плеча . На количество опытов в центре плана  при этом не накладывается никаких ограничений. В этом случае  обычно принимают равным единице.

Возьмем матрицу композиционного планирования для , положив  (табл. 3.10).

В общем виде приведенная матрица неортогональна, так как:

 и .

Таблица 3.10

№ опыта
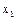
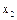
1	+1	+1	+1	+1	+1	+1
2	+1	+1	-1	-1	+1	+1
3	+1	-1	-1	+1	+1	+1
4	+1	-1	+1	-1	+1	+1
5	+1	+a	0	0	a2	0
6	+1	-a	0	0	a2	0
7	+1	0	+a	0	0	a2
8	+1	0	-a	0	0	a2
9	+1	0	0	0	0	0

Приведем матрицу к ортогональному виду. Для этого преобразуем квадратичные переменные:

.

При этом

, но .

Чтобы сделать матрицу планирования полностью ортогональной, величину звездного плеча  выбирают из условия равенства нулю недиагонального члена корреляционной матрицы .

В табл. 3.11 приведены значения  для различного числа факторов.

Таблица 3. 11

	Число независимых факторов k
	2	3	4	5
“Ядро” плана
	1.00	1.215	1.414	1.547

Ортогональная матрица 2-го порядка для принимает вид (табл. 3.12).

Таблица 3. 12

№ опыта
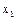
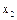
1	+1	+1	+1	+1	+1/3	+1/3
2	+1	+1	-1	-1	+1/3	+1/3
3	+1	-1	-1	+1	+1/3	+1/3
4	+1	-1	+1	-1	+1/3	+1/3
5	+1	+1	0	0	+1/3	-2/3
6	+1	-1	0	0	+1/3	-2/3
7	+1	0	+1	0	-2/3	+1/3
8	+1	0	-1	0	-2/3	+1/3
9	+1	0	0	0	-2/3	-2/3

В силу ортогональности матрицы планирования все коэффициенты регрессии определяются независимо друг от друга по формуле:

                                                                 (11)

и дисперсии коэффициентов равны:

.                                                                    (12)

В результате расчетов по матрице с преобразованными столбцами для квадратичных эффектов получим уравнение вида

.

Чтобы перейти к обычной записи, определяют b₀ по формуле:

и оценивают с дисперсией, равной

.

Зная , проверяют значимость коэффициентов и адекватность уравнения

.

Адекватность уравнения проверяют по критерию Фишера, составляя отношение . Уравнение адекватно, если F-отношение меньше табулированного

,

где р – уровень значимости (обычно );  – число степеней свободы остаточной дисперсии;  – число степеней свободы дисперсии воспроизводимости; N – число опытов в матрице планирования; L – число коэффициентов в уравнении регрессии второго порядка.