 |
Главная |
Решение прямой задачи для вала с n-дисками
|
из
5.00
|
Рассмотрим вал, несущий п- дисков. Пусть углы закручивания вала в местах насадки диска будут соответственно 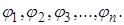 Жесткости I, II,..., n-1 участков вала, т. е. на основе обозначения (1.1) моменты, которые могут вызвать угол закручивания данного участка равный одному радиану, обозначим: k1, k2,…, kп-1. Моменты инерции дисков по-прежнему обозначим I1,I2,..,In. Для получения уравнения колебательного движения рассматриваемой нами системы применим уравнения Лагранжа, при пользовании которыми необходимо знать выражение для кинетической и потенциальной энергии системы. Кинетическая энергия диска, имеющего момент инерции I и угол закручивания
Жесткости I, II,..., n-1 участков вала, т. е. на основе обозначения (1.1) моменты, которые могут вызвать угол закручивания данного участка равный одному радиану, обозначим: k1, k2,…, kп-1. Моменты инерции дисков по-прежнему обозначим I1,I2,..,In. Для получения уравнения колебательного движения рассматриваемой нами системы применим уравнения Лагранжа, при пользовании которыми необходимо знать выражение для кинетической и потенциальной энергии системы. Кинетическая энергия диска, имеющего момент инерции I и угол закручивания 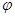 , выражается формулой
, выражается формулой
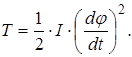
Кинетическая энергия нашей системы слагается из суммы кинетической энергии всех дисков (кинетическую энергию вала мы тут не учитываем, считая момент инерции диска большим по сравнению с моментом инерции вала).
Кинетическая энергия всей системы
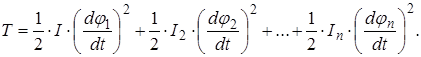 (2.6)
(2.6)
Для нахождения потенциальной энергии системы, являющейся в данном случае энергией кручения, необходимо пользоваться формулой
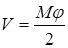 ,
,
где М - крутящий момент, действующий на данном участке, а 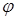 - угол закручивания того же участка. Найдем крутящий момент и угол закручивания для первого участка нашей системы.
- угол закручивания того же участка. Найдем крутящий момент и угол закручивания для первого участка нашей системы.
Если в месте насадки первого диска угол закручивания 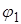 , а в месте насадки второго диска —
, а в месте насадки второго диска — 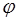 2, то угол закручивания на участке вала между дисками будет:
2, то угол закручивания на участке вала между дисками будет:
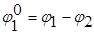 (2.7)
(2.7)
Для того чтобы вызвать угол закручивания первого участка вала величиной в I радиан, необходимо приложить крутящий момент величины k1, если же, как в нашем случае угол закручивания имеет 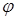 1-
1- 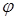 2 радиан, то на валу действует крутящий момент величины
2 радиан, то на валу действует крутящий момент величины
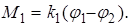
В нашем случае углы закручивания для участков вала будут:
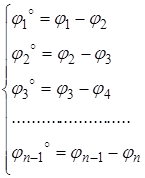 (2.8)
(2.8)
и крутящие моменты:
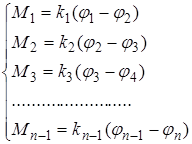 (2.9)
(2.9)
Теперь можем составить выражение для потенциальной энергии системы, суммируя потенциальную энергию участков.
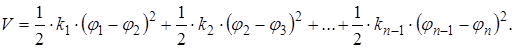 (2.10)
(2.10)
(так как 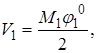 то, подставляя значения
то, подставляя значения 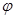 1 из (2.8) и M1 из (2.9) и аналогично для других участков получим формулу (2.10)).
1 из (2.8) и M1 из (2.9) и аналогично для других участков получим формулу (2.10)).
В данном случае система имеет п степеней свободы, чему соответствует п обобщенных координат. Обобщенными координатами являются углы закручивания вала в местах насадки дисков. Уравнение Лагранжа, очевидно, придется составить по числу степеней свободы, т. е. также п. Для пользования уравнением Лагранжа в виде
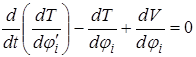 (2.11)
(2.11)
необходимо найти частные производные от кинетической и потенциальной энергии системы, по обобщенным координатам 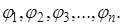 и частные производные от кинетической энергии по дифференциалам обобщенных координат:
и частные производные от кинетической энергии по дифференциалам обобщенных координат:
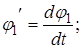
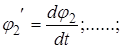
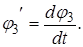
Дифференцируя уравнение (2.6) найдем:
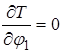 ;
; 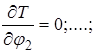
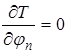
и дифференцируя уравнение (2.10)
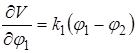 ;
; 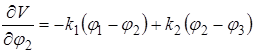 ;
;
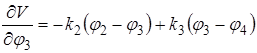 ;……;
;……; 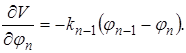
Дифференцируя уравнение (2.6) по 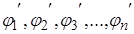 получим:
получим:
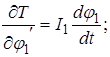
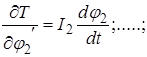
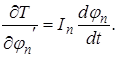
Полученные уравнения необходимо продифференцировать по времени
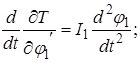
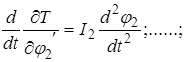
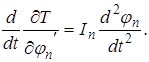
Располагая найденными выше величинами, можем составить систему дифференциальных уравнений движения рассматриваемой системы.
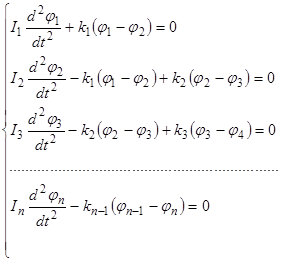 (2.12)
(2.12)
Для решения полученной системы дифференциальных уравнений полагаем, что каждое колебательное движение системы (их будет столько же, сколько и степеней свободы, т. е. п) будет простым гармоническим. Частные решения системы (2.12), можно представить в виде:
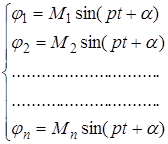 . (2.13)
. (2.13)
В этих уравнениях по-прежнему М амплитуда колебания, и р частота. Находим вторую производную от 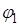 по времени:
по времени:
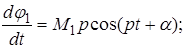
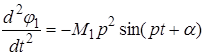 .
.
Аналогично,
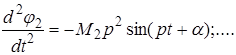
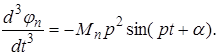
Подставляя значения 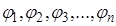 и
и 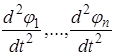 в уравнения системы (2.12), получим систему обыкновенных уравнений со многими неизвестными для определения частоты колебания р.
в уравнения системы (2.12), получим систему обыкновенных уравнений со многими неизвестными для определения частоты колебания р.
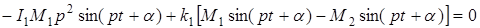
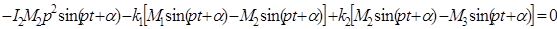
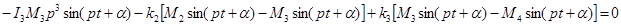
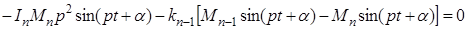
Сокращая в данных уравнениях на 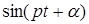 получим окончательно
получим окончательно
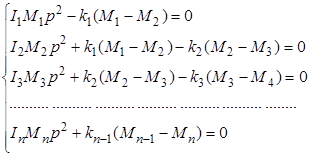 (2.14)
(2.14)
Последовательно исключая неизвестные 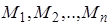 , получим уравнение для определения частоты р. Уравнение для определения частоты собственных колебаний, полученное в результате исключения
, получим уравнение для определения частоты р. Уравнение для определения частоты собственных колебаний, полученное в результате исключения 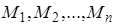 из уравнений (2.14), называется характеристическим. Уравнения (2.14) могут быть применены для определения числа собственных крутильных колебаний системы с произвольным числом дисков. В тех случаях, когда получившееся характеристическое уравнение имеет высокую степень относительно р2 (что бывает при системе со многими дисками), оно может быть решено графически либо каким-нибудь приближенным методом.
из уравнений (2.14), называется характеристическим. Уравнения (2.14) могут быть применены для определения числа собственных крутильных колебаний системы с произвольным числом дисков. В тех случаях, когда получившееся характеристическое уравнение имеет высокую степень относительно р2 (что бывает при системе со многими дисками), оно может быть решено графически либо каким-нибудь приближенным методом.
|
из
5.00
|
Обсуждение в статье: Решение прямой задачи для вала с n-дисками |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

