 |
Главная |
Некоторые базисные леммы
|
из
5.00
|
В теории конечных групп одним из основных понятий является понятие субнормальности подгрупп, введенное Виландтом в работе [73].
Напомним, что подгруппа  называется субнормальной подгруппой группы
называется субнормальной подгруппой группы  , если существует цепь подгрупп
, если существует цепь подгрупп

такая, что для любого  подгруппа
подгруппа  нормальна в
нормальна в  .
.
Естественным обобщением понятия субнормальности является понятие  -субнормальности, которое для произвольных конечных групп впервые введено Л.А. Шеметковым в монографии [44].
-субнормальности, которое для произвольных конечных групп впервые введено Л.А. Шеметковым в монографии [44].
Пусть  --- непустая формация. Подгруппу
--- непустая формация. Подгруппу  группы
группы  называют
называют  -субнормальной, если либо
-субнормальной, если либо  , либо существует максимальная цепь
, либо существует максимальная цепь

такая, что  для всех
для всех  .
.
Несколько другое понятие  -субнормальности введено Кегелем в работе [69]. Фактически оно объединяет понятие субнормальности и
-субнормальности введено Кегелем в работе [69]. Фактически оно объединяет понятие субнормальности и  -субнормальности в смысле Шеметкова.
-субнормальности в смысле Шеметкова.
Подгруппу  называют
называют  -субнормальной в смысле Кегеля или
-субнормальной в смысле Кегеля или  -достижимой, если существует цепь подгрупп
-достижимой, если существует цепь подгрупп

такая, что для любого  либо подгруппа
либо подгруппа  нормальна в
нормальна в  , либо
, либо  .
.
Для любой непустой формации  множество всех
множество всех  -достижимых подгрупп произвольной группы
-достижимых подгрупп произвольной группы  содержит множество всех субнормальных подгрупп группы
содержит множество всех субнормальных подгрупп группы  и множество всех
и множество всех  -субнормальных подгрупп группы
-субнормальных подгрупп группы  . Если же
. Если же  --- непустая нильпотентная формация, то множество всех
--- непустая нильпотентная формация, то множество всех  -достижимых подгрупп в точности совпадает с множеством всех субнормальных подгрупп для любой группы
-достижимых подгрупп в точности совпадает с множеством всех субнормальных подгрупп для любой группы  .
.
В Коуровской тетради [10] Л.А. Шеметковым была поставлена проблема классификации сверхрадикальных формаций.
Напомним, что формация  называется сверхрадикальной, если она удовлетворяет следующим требованиям:
называется сверхрадикальной, если она удовлетворяет следующим требованиям:
1)  --- нормально наследственная формация;
--- нормально наследственная формация;
2) любая группа  , где
, где  и
и  ---
---  -субнормальные
-субнормальные  -подгруппы из
-подгруппы из  , принадлежит
, принадлежит  .
.
В.Н. Семенчуком в работе [28] в классе конечных разрешимых групп было получено полное решение данной проблемы.
В данной главе получено полное решение проблемы Шеметкова для наследственных насыщенных формаций, критические группы которых разрешимы
В данном разделе приводятся некоторые свойства критических групп (минимальных не  -групп) и обобщенно субнормальных (
-групп) и обобщенно субнормальных (  -субнормальных и
-субнормальных и  -достижимых) подгрупп, которые будут использоваться при доказательстве основных результатов диссертации.
-достижимых) подгрупп, которые будут использоваться при доказательстве основных результатов диссертации.
Напомним, что критической группой формации  ( минимальной не
( минимальной не  -группой) называется группа, не принадлежащая
-группой) называется группа, не принадлежащая  , все собственные подгруппы которой принадлежат
, все собственные подгруппы которой принадлежат  . Множество всех таких групп обозначают
. Множество всех таких групп обозначают  . Через
. Через  обозначают множество всех разрешимых групп, а через
обозначают множество всех разрешимых групп, а через 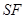 --- множество всех групп, у которых
--- множество всех групп, у которых  -корадикал
-корадикал  разрешим.
разрешим.
1.1 Лемма. Пусть  --- насыщенная формация,
--- насыщенная формация,  --- наследственная насыщенная формация. Если
--- наследственная насыщенная формация. Если  и
и  , где
, где  , то
, то  .
.
Доказательство. Пусть  . По теореме 2.2.1,
. По теореме 2.2.1,  ---
---  -группа. Очевидно, что
-группа. Очевидно, что  . По лемме 2.2.2,
. По лемме 2.2.2,  , где
, где 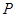 ---
---  -группа,
-группа,  ---
---  -группа и
-группа и  . Так как
. Так как 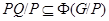 и
и  , то
, то  . Следовательно,
. Следовательно,  ---
---  -группа. Пусть
-группа. Пусть  ---
---  -главный фактор
-главный фактор  . Если
. Если  ---
---  -группа, то
-группа, то 
 -централен.
-централен.
Пусть  ---
---  -группа. По теореме 2.2.3,
-группа. По теореме 2.2.3,  . Пусть
. Пусть  и
и  --- произвольная
--- произвольная  -абнормальная максимальная подгруппа группы
-абнормальная максимальная подгруппа группы  . Тогда
. Тогда  . Так как
. Так как  , то, по теореме 2.2.4,
, то, по теореме 2.2.4,  . Следовательно,
. Следовательно,  . Поскольку
. Поскольку

то  . Учитывая, что
. Учитывая, что  , по теореме 2.2.5, имеем
, по теореме 2.2.5, имеем

где  --- максимальные внутренние локальные экраны, соответственно
--- максимальные внутренние локальные экраны, соответственно  и
и 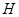 . Если
. Если  , то
, то  . Отсюда и из того, что
. Отсюда и из того, что

следует 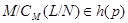 . А это значит, что
. А это значит, что 
 -централен.
-централен.
Пусть  . Так как
. Так как  --- насыщенная формация и
--- насыщенная формация и  , то
, то  . Следовательно,
. Следовательно,  ---
---  -нормализатор группы
-нормализатор группы  . В силу того, что
. В силу того, что  покрывает
покрывает  , то
, то 
 -централен. Следовательно,
-централен. Следовательно,  . По теореме 2.2.4,
. По теореме 2.2.4,  . Лемма доказана.
. Лемма доказана.
1.2 Лемма. Пусть  --- непустая наследственная формация. Если
--- непустая наследственная формация. Если 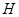 ---
---  -субнормальная подгруппа, то
-субнормальная подгруппа, то  --- субнормальная подгруппа.
--- субнормальная подгруппа.
Доказательство. Пусть  ---
---  -субнормальная подгруппа группы
-субнормальная подгруппа группы  . Если
. Если  , то лемма очевидна. Пусть
, то лемма очевидна. Пусть  . Тогда
. Тогда  содержится в максимальной
содержится в максимальной  -нормальной подгруппе
-нормальной подгруппе  группы
группы  . По индукции,
. По индукции,  --- субнормальная подгруппа из
--- субнормальная подгруппа из  . Так как
. Так как 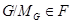 и
и  --- наследственная формация, то
--- наследственная формация, то  . Следовательно,
. Следовательно,  , значит,
, значит,  . Поскольку
. Поскольку 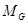 --- нормальная подгруппа группы
--- нормальная подгруппа группы  , то
, то  --- субнормальная подгруппа
--- субнормальная подгруппа  . Лемма доказана.
. Лемма доказана.
1.3 Лемма. Пусть  --- наследственная насыщенная формация,
--- наследственная насыщенная формация, 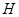 ---
---  -субнормальная подгруппа группы
-субнормальная подгруппа группы  такая, что
такая, что  . Тогда
. Тогда 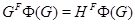 .
.
Доказательство. Пусть  . Очевидно,
. Очевидно,

Так как  , то по индукции
, то по индукции  . Следовательно,
. Следовательно,

Отсюда, согласно лемме 2.2.6,

Пусть  . Тогда
. Тогда  --- цоколь группы
--- цоколь группы  . По лемме 3.1.2,
. По лемме 3.1.2,  --- субнормальная подгруппа группы
--- субнормальная подгруппа группы  . По теореме 2.2.7,
. По теореме 2.2.7,  . Следовательно,
. Следовательно,  --- нормальная подгруппа группы
--- нормальная подгруппа группы  . Тогда
. Тогда

По теореме 2.2.8,  . Отсюда следует, что
. Отсюда следует, что 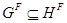 . Так как
. Так как  и
и  --- наследственная формация, то
--- наследственная формация, то  . Получаем
. Получаем  , т. е.
, т. е.  . Лемма доказана.
. Лемма доказана.
В следующих леммах приводятся основные свойства  -субнормальных подгрупп.
-субнормальных подгрупп.
1.4 Лемма. Пусть  --- непустая наследственная формация. Тогда справедливы следующие утверждения:
--- непустая наследственная формация. Тогда справедливы следующие утверждения:
1) если  --- подгруппа группы
--- подгруппа группы  и
и  , то
, то  ---
---  -субнормальная (
-субнормальная (  -достижимая) подгруппа группы
-достижимая) подгруппа группы  ;
;
2) если  ---
---  -субнормальная (
-субнормальная (  -достижимая) подгруппа группы
-достижимая) подгруппа группы  , то
, то 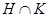 ---
---  -субнормальная (
-субнормальная (  -достижимая) подгруппа
-достижимая) подгруппа  для любой подгруппы
для любой подгруппы 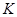 группы
группы  ;
;
3) если  ---
---  -субнормальная (
-субнормальная (  -достижимая) подгруппа
-достижимая) подгруппа 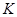 и
и 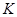 ---
---  -субнормальная (
-субнормальная (  -достижимая) подгруппа группы
-достижимая) подгруппа группы  , то
, то  ---
---  -субнормальная (
-субнормальная (  -достижимая) подгруппа группы
-достижимая) подгруппа группы  ;
;
4) если  и
и 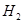 ---
---  -субнормальные (
-субнормальные (  -достижимые) подгруппы группы
-достижимые) подгруппы группы  , то
, то  ---
---  -субнормальная (
-субнормальная (  -достижимая) подгруппа группы
-достижимая) подгруппа группы  ;
;
5) если все композиционные факторы группы  принадлежат формации
принадлежат формации  , то каждая субнормальная подгруппа группы
, то каждая субнормальная подгруппа группы 
 -субнормальна в
-субнормальна в  ;
;
6) если  ---
---  -субнормальная (
-субнормальная (  -достижимая) подгруппа группы
-достижимая) подгруппа группы  , то
, то 
 -субнормальна (
-субнормальна (  -достижима) в
-достижима) в  для любых
для любых  .
.
Доказательство. 1) Пусть  --- подгруппа группы
--- подгруппа группы  и
и 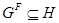 . Так как
. Так как  и
и  --- наследственная формация, то подгруппа
--- наследственная формация, то подгруппа  является
является  -субнормальной подгруппой группы
-субнормальной подгруппой группы  . Отсюда, согласно определению
. Отсюда, согласно определению  -субнормальной подгруппы, существует максимальная цепь
-субнормальной подгруппы, существует максимальная цепь
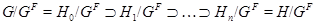
такая, что  для всех
для всех  . Отсюда, с учетом леммы 2.2.6 получаем, что в группе
. Отсюда, с учетом леммы 2.2.6 получаем, что в группе  существует максимальная цепь
существует максимальная цепь

такая, что  для всех
для всех  .
.
А это значит, что  ---
--- 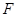 -субнормальная подгруппа группы
-субнормальная подгруппа группы  .
.
Пусть  --- подгруппа группы
--- подгруппа группы  , содержащая
, содержащая  , тогда
, тогда  ---
---  -субнормальная подгруппа группы
-субнормальная подгруппа группы  . А так как любая
. А так как любая 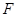 -субнормальная подгруппа группы
-субнормальная подгруппа группы  является
является 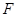 -достижимой в
-достижимой в  , то
, то  ---
--- 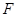 -достижимая подгруппа группы
-достижимая подгруппа группы  .
.
2) Пусть  ---
--- 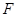 -субнормальная подгруппа группы
-субнормальная подгруппа группы  . Тогда, по определению, существует максимальная цепь подгрупп
. Тогда, по определению, существует максимальная цепь подгрупп

такая, что для любого 
 .
.
Пусть 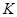 --- некоторая подгруппа из
--- некоторая подгруппа из  . Рассмотрим цепь подгрупп
. Рассмотрим цепь подгрупп

Так как  и формация
и формация 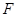 наследственна, то из
наследственна, то из  следует, что
следует, что
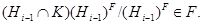
Теперь, ввиду изоморфизма,

имеем  . Значит,
. Значит,  . Так как
. Так как  , то
, то  . Итак,
. Итак, 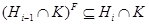 . Отсюда, по определению,
. Отсюда, по определению, 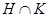 ---
---  -субнормальная подгруппа группы
-субнормальная подгруппа группы  .
.
Пусть  ---
---  -достижимая подгруппа группы
-достижимая подгруппа группы  . Тогда, по определению, существует цепь подгрупп
. Тогда, по определению, существует цепь подгрупп

такая, что для любого  либо подгруппа
либо подгруппа  нормальна в
нормальна в  , либо
, либо  .
.
Пусть  --- некоторая подгруппа из
--- некоторая подгруппа из  . Рассмотрим цепь подгрупп:
. Рассмотрим цепь подгрупп:

Если подгруппа  нормальна в
нормальна в  , то подгруппа
, то подгруппа  нормальна в
нормальна в  . Пусть
. Пусть  . Так как формация
. Так как формация  наследственна, то из
наследственна, то из  следует, что
следует, что
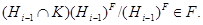
Теперь, ввиду изоморфизма,

имеем  . Значит,
. Значит,  . Так как
. Так как  , то
, то 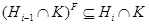 . Итак, для каждого
. Итак, для каждого  либо подгруппа
либо подгруппа  нормальна в
нормальна в  , либо
, либо  . Отсюда, по определению,
. Отсюда, по определению,  ---
---  -достижимая подгруппа группы
-достижимая подгруппа группы  .
.
Утверждение 3) следует непосредственно из определения  -субнормальной (
-субнормальной (  -достижимой) подгруппы.
-достижимой) подгруппы.
Утверждение 4) следует теперь из утверждений 2) и 3).
5) Пусть все композиционные факторы группы  принадлежат формации
принадлежат формации  , и пусть
, и пусть  --- субнормальная подгруппа группы
--- субнормальная подгруппа группы 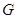 . Тогда в группе
. Тогда в группе  существует цепь подгрупп
существует цепь подгрупп

такая, что для любого  подгруппа
подгруппа  нормальна в
нормальна в  .
.
Согласно условию,  , отсюда следует, что
, отсюда следует, что  . А это значит, что подгруппа
. А это значит, что подгруппа 
 -субнормальна в группе
-субнормальна в группе  .
.
Утверждение 6) следует непосредственно из определения  -субнормальной (
-субнормальной (  -достижимой) подгруппы. Лемма доказана.
-достижимой) подгруппы. Лемма доказана.
1.5 Лемма. Пусть  --- непустая формация,
--- непустая формация,  и
и  --- подгруппы группы
--- подгруппы группы  , причем
, причем  нормальна в
нормальна в 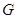 . Тогда:
. Тогда:
1) если 
 -субнормальна (
-субнормальна (  -достижима) в
-достижима) в  , то
, то 
 -субнормальна (
-субнормальна (  -достижима) в
-достижима) в  и
и 
 -субнормальна (
-субнормальна (  -достижима) в
-достижима) в  ;
;
2) если  , то
, то 
 -субнормальна (
-субнормальна (  -достижима) в
-достижима) в  тогда и только тогда, когда
тогда и только тогда, когда 
 -субнормальна (
-субнормальна (  -достижима) в
-достижима) в  .
.
Доказательство. Пусть  ---
---  -субнормальная подгруппа группы
-субнормальная подгруппа группы  . Тогда, по определению, существует максимальная цепь подгрупп
. Тогда, по определению, существует максимальная цепь подгрупп

такая, что для любого 
 .
.
Рассмотрим следующую цепь подгрупп

Так как  , то ввиду леммы 2.2.6,
, то ввиду леммы 2.2.6,  . Отсюда следует, что
. Отсюда следует, что
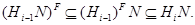
Итак, для каждого 
 . Отсюда, по определению,
. Отсюда, по определению,  ---
---  -субнормальная подгруппа группы
-субнормальная подгруппа группы  .
.
Ввиду леммы 2.2.6,

Поэтому для любого 
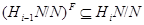 . Значит,
. Значит,  ---
---  -субнормальная подгруппа группы
-субнормальная подгруппа группы  .
.
Пусть  ---
---  -достижимая подгруппа группы
-достижимая подгруппа группы  . Тогда, по опрeделению, существует цепь подгрупп
. Тогда, по опрeделению, существует цепь подгрупп

такая, что для любого  либо
либо 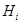 нормальна в
нормальна в  , либо
, либо 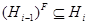 . Рассмотрим следующую цепь подгрупп
. Рассмотрим следующую цепь подгрупп

Если подгруппа 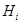 нормальна в
нормальна в  , то подгруппа
, то подгруппа  нормальна в
нормальна в  . Пусть
. Пусть  . Тогда ввиду леммы 2.2.6,
. Тогда ввиду леммы 2.2.6,  . Отсюда следует, что
. Отсюда следует, что 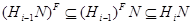 . Итак, для каждого
. Итак, для каждого  либо подгруппа
либо подгруппа  нормальна в
нормальна в  , либо
, либо  . Отсюда, по определению,
. Отсюда, по определению,  ---
---  -достижимая подгруппа группы
-достижимая подгруппа группы  .
.
Ввиду леммы 2.2.6, 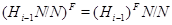 . Поэтому для любого
. Поэтому для любого  либо подгруппа
либо подгруппа 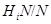 нормальна в
нормальна в  , либо
, либо 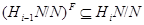 . Значит,
. Значит,  ---
---  -достижимая подгруппа группы
-достижимая подгруппа группы  .
.
Утверждение 2) следует из 1) и леммы 2.2.6. Лемма доказана.
|
из
5.00
|
Обсуждение в статье: Некоторые базисные леммы |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

