 |
Главная |
Сверхрадикальные формации
|
из
5.00
|
В теории формаций конечных групп одной из известных проблем является проблема Шеметкова об описании сверхрадикальных формаций.
В.Н. Семенчуком в работе [28] получено полное решение проблемы Л.А. Шеметкова в классе конечных разрешимых групп. Оказалось, что все такие формации имеют следующее строение:  , где
, где  --- некоторые множества простых чисел, а
--- некоторые множества простых чисел, а  --- множество всех разрешимых
--- множество всех разрешимых 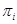 -групп.
-групп.
В данном разделе приводится описание наследственных насыщенных сверхрадикальных формаций, критические группы которых разрешимы.
Приведем примеры сверхрадикальных формаций.
3.1 Пример. Формация всех  -групп
-групп 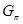 , где
, где  --- некоторое множество простых чисел является сверхрадикальной формацией.
--- некоторое множество простых чисел является сверхрадикальной формацией.
Действительно. Пусть  , где
, где  и
и  ---
---  -группы,
-группы, 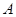 и
и  ---
---  -субнормальные подгруппы группы
-субнормальные подгруппы группы  . Так как формация
. Так как формация  замкнута относительно расширений, то, очевидно, что
замкнута относительно расширений, то, очевидно, что  ---
---  -группа.
-группа.
3.2 Пример. Формации  ,
,  --- сверхрадикальные формации.
--- сверхрадикальные формации.
Действительно, если  ---
---  -субнормальная подгруппа группы
-субнормальная подгруппа группы  , то
, то 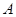 --- субнормальная подгруппа из
--- субнормальная подгруппа из  . Очевидно, что любая группа
. Очевидно, что любая группа  , где
, где 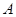 и
и  --- нильпотентные субнормальные подгруппы из
--- нильпотентные субнормальные подгруппы из  , нильпотентна.
, нильпотентна.
Если  --- разрешимая
--- разрешимая  -субнормальная подгруппа из
-субнормальная подгруппа из 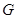 , то
, то 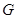 разрешима. Следовательно,
разрешима. Следовательно,  --- сверхрадикальная формация.
--- сверхрадикальная формация.
Аналогичным образом доказывается, что любая нормально наследственная, замкнутая относительно расширений, формация является сверхрадикальной.
Следующая лемма устанавливает связь между сверхрадикальными формациями и формациями Фиттинга.
Напомним, что формациями Фиттинга  называются формации, которые замкнуты относительно взятия субнормальных подгрупп и произведения нормальных
называются формации, которые замкнуты относительно взятия субнормальных подгрупп и произведения нормальных  -подгрупп.
-подгрупп.
3.3 Лемма. Пусть  --- наследственная сверхрадикальная формация, тогда
--- наследственная сверхрадикальная формация, тогда  --- формация Фиттинга.
--- формация Фиттинга.
Доказательство. Пусть  , где
, где  и
и  --- нормальные
--- нормальные  -подгруппы группы
-подгруппы группы 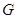 . Так как
. Так как

то  . Аналогичным образом,
. Аналогичным образом,  . Согласно лемме 3.1.4,
. Согласно лемме 3.1.4, 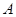 и
и  ---
---  -субнормальные подгруппы группы
-субнормальные подгруппы группы 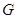 . Так как
. Так как  --- сверхрадикальная формация, то
--- сверхрадикальная формация, то  . Итак,
. Итак,  --- формация Фиттинга. Лемма доказана.
--- формация Фиттинга. Лемма доказана.
3.4 Лемма. Пусть  --- непустая наследственная формация. Если
--- непустая наследственная формация. Если  содержит любую группу
содержит любую группу  , где для любого
, где для любого  из
из  силовские
силовские  -подгруппы
-подгруппы  и
и  принадлежат
принадлежат  и
и  -субнормальные подгруппы в
-субнормальные подгруппы в  , то
, то  --- сверхрадикальная формация.
--- сверхрадикальная формация.
Доказательство. Пусть  --- непустая наследственная формация, удовлетворяющая условию леммы. Покажем, что
--- непустая наследственная формация, удовлетворяющая условию леммы. Покажем, что  --- сверхрадикальная формация. Пусть
--- сверхрадикальная формация. Пусть  , где
, где  и
и  ---
---  -субнормальные
-субнормальные  -подгруппы группы
-подгруппы группы  . Пусть
. Пусть  --- произвольное простое число из
--- произвольное простое число из  , а
, а  и
и 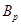 --- силовские
--- силовские  -подгруппы из
-подгруппы из 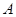 и
и  соответственно. Так как
соответственно. Так как  и
и  принадлежат
принадлежат  и
и  --- наследственная формация, то
--- наследственная формация, то  и
и  принадлежат
принадлежат  и,
и,  и
и 
 -субнормальны в
-субнормальны в  и
и  соответственно. Так как
соответственно. Так как  и
и  ---
---  -субнормальные подгруппы группы
-субнормальные подгруппы группы 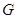 , то согласно лемме 3.1.4,
, то согласно лемме 3.1.4,  и
и 
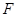 -субнормальны в группе
-субнормальны в группе  . Согласно условию леммы,
. Согласно условию леммы,  принадлежит
принадлежит  . А это значит, что
. А это значит, что  --- сверхрадикальная формация. Лемма доказана.
--- сверхрадикальная формация. Лемма доказана.
3.5 Лемма. Пусть  --- наследственная насыщенная разрешимая формация. Тогда следующие утверждения эквивалентны:
--- наследственная насыщенная разрешимая формация. Тогда следующие утверждения эквивалентны:
1)  --- сверхрадикальная формация;
--- сверхрадикальная формация;
2)  --- содержит любую группу
--- содержит любую группу  , где
, где 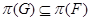 и для любого простого числа
и для любого простого числа  из
из 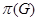 силовские
силовские  -подгруппы
-подгруппы  и
и 
 -субнормальны в
-субнормальны в  .
.
Доказательство. Покажем, что из 1) следует 2).
Пусть  --- сверхрадикальная формация и пусть
--- сверхрадикальная формация и пусть  , где
, где  и для любого простого числа
и для любого простого числа  из
из 
 и
и 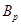 ---
---  -субнормальные подгруппы группы
-субнормальные подгруппы группы 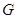 . Так как
. Так как  --- насыщенная формация и
--- насыщенная формация и  , то
, то  и
и  принадлежат
принадлежат  . Так как
. Так как  --- разрешимая формация и
--- разрешимая формация и  ---
---  -субнормальная подгруппа группы
-субнормальная подгруппа группы  , то отсюда нетрудно показать, что
, то отсюда нетрудно показать, что  --- разрешимая группа. А это значит, что
--- разрешимая группа. А это значит, что 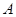 и
и  разрешимы.
разрешимы.
Согласно теореме Ф. Холла [63],  , где
, где 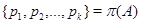 . Так как
. Так как  --- сверхрадикальная формация, то
--- сверхрадикальная формация, то  принадлежит
принадлежит  . Так как
. Так как  и
и  ---
---  -субнормальные подгруппы группы
-субнормальные подгруппы группы 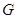 , то согласно теореме 2.2.10,
, то согласно теореме 2.2.10,  ---
---  -субнормальная подгруппа группы
-субнормальная подгруппа группы 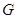 . Так как
. Так как  принадлежит
принадлежит  и
и  --- сверхрадикальная формация, то подгруппа
--- сверхрадикальная формация, то подгруппа  принадлежит
принадлежит  . Продолжая в аналогичном порядке получаем, что
. Продолжая в аналогичном порядке получаем, что  принадлежит
принадлежит  . Аналогичным образом можем доказать, что
. Аналогичным образом можем доказать, что  принадлежит
принадлежит  . Так как
. Так как  --- сверхрадикальная формация, то
--- сверхрадикальная формация, то  .
.
Тот факт, что из 2) следует 1) вытекает из леммы 3.3.4. Лемма доказана.
В следующей теореме получено решение проблемы Шеметкова о классификации сверхрадикальных формаций для наследственных насыщенных формаций, критические группы которых разрешимы.
3.6 Теорема [20-A]. Пусть  --- наследственная насыщенная формация такая, что
--- наследственная насыщенная формация такая, что  . Тогда следующие утверждения эквивалентны:
. Тогда следующие утверждения эквивалентны:
1) 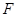 --- сверхрадикальная формация;
--- сверхрадикальная формация;
2)  , где
, где  --- некоторые множества простых чисел.
--- некоторые множества простых чисел.
Доказательство. Пусть  --- сверхрадикальная формация. Вначале докажем, что любая минимальная не
--- сверхрадикальная формация. Вначале докажем, что любая минимальная не  -группа является либо группой простого порядка, либо группой Шмидта.
-группа является либо группой простого порядка, либо группой Шмидта.
Пусть 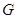 --- произвольная минимальная не
--- произвольная минимальная не 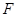 -группа. Согласно условию теоремы,
-группа. Согласно условию теоремы, 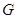 разрешима. Если
разрешима. Если  , то нетрудно заметить, что
, то нетрудно заметить, что  --- группа простого порядка
--- группа простого порядка  , где
, где  .
.
Рассмотрим случай, когда  . Согласно теореме 2.2.5,
. Согласно теореме 2.2.5,  , где
, где  --- единственная минимальная нормальная подгруппа из
--- единственная минимальная нормальная подгруппа из  ,
,  ---
---  -группа,
-группа,  ,
,  --- максимальный внутренний локальный экран формации
--- максимальный внутренний локальный экран формации  . Очевидно, что
. Очевидно, что  .
.
Покажем, что  является примарной циклической подгруппой. Предположим противное. Поскольку
является примарной циклической подгруппой. Предположим противное. Поскольку  --- разрешимая группа, то в
--- разрешимая группа, то в  существуют максимальные подгруппы
существуют максимальные подгруппы  и
и  такие, что
такие, что 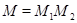 . Так как
. Так как  , то очевидно, что
, то очевидно, что  и
и  ---
---  -нормальные максимальные
-нормальные максимальные  -подгруппы группы
-подгруппы группы 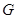 . Но тогда
. Но тогда  . Так как
. Так как  --- сверхрадикальная формация, то
--- сверхрадикальная формация, то  . Противоречие. Итак,
. Противоречие. Итак,  имеет единственный класс максимальных сопряженных подгрупп. Следовательно,
имеет единственный класс максимальных сопряженных подгрупп. Следовательно,  --- циклическая
--- циклическая  -подгруппа. Поскольку
-подгруппа. Поскольку  --- насыщенная формация и
--- насыщенная формация и  , имеем
, имеем  .
.
Покажем, что  . Предположим противное. Пусть
. Предположим противное. Пусть  , где
, где  . Пусть
. Пусть  и
и  --- циклические группы соответственно порядков
--- циклические группы соответственно порядков 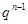 и
и  . Обозначим через
. Обозначим через  регулярное сплетение
регулярное сплетение 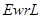 . Пусть
. Пусть  --- база сплетения, т. е.
--- база сплетения, т. е.  . Так как некоторая подгруппа группы
. Так как некоторая подгруппа группы  изоморфна
изоморфна  , то
, то  . Очевидно, подгруппы
. Очевидно, подгруппы  ,
,  принадлежат формации
принадлежат формации 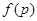 .
.
Пусть  , где
, где  . Обозначим через
. Обозначим через 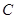 базу сплетения
базу сплетения  . Тогда
. Тогда  .
.
Так как  , то
, то  , значит, что подгруппы
, значит, что подгруппы  и
и 
 -субнормальны в
-субнормальны в  . Легко видеть, что
. Легко видеть, что  ,
,  .
.
Так как  --- сверхрадикальная формация, то
--- сверхрадикальная формация, то  . Но
. Но  , и поэтому
, и поэтому  .
.
Полученное противоречие показывает, что  . Итак,
. Итак,  --- группа Шмидта. Теперь из леммы 3.1.1 следует, что
--- группа Шмидта. Теперь из леммы 3.1.1 следует, что  --- группа Шмидта.
--- группа Шмидта.
Пусть  --- максимальный внутренний локальный экран формации
--- максимальный внутренний локальный экран формации  . Покажем, что формация
. Покажем, что формация  имеет полный локальный экран
имеет полный локальный экран  такой, что
такой, что 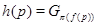 , для любого
, для любого  из
из 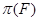 . Действительно, пусть
. Действительно, пусть 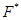 --- такая формация, у которой есть локальный экран
--- такая формация, у которой есть локальный экран 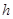 . Покажем, что
. Покажем, что  .
.
С учетом того, что  для любого простого
для любого простого  из
из  , получим
, получим  .
.
Покажем обратное включение. Пусть 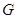 --- группа наименьшего порядка из
--- группа наименьшего порядка из  . Так как
. Так как  --- наследственная формация, то формация
--- наследственная формация, то формация  также является наследственной, значит,
также является наследственной, значит, 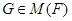 . Так как
. Так как  --- насыщенная формация, то нетрудно показать, что
--- насыщенная формация, то нетрудно показать, что  .
.
Выше показано, что  --- либо группа простого порядка, либо группа Шмидта. Пусть
--- либо группа простого порядка, либо группа Шмидта. Пусть 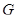 --- группа простого порядка и
--- группа простого порядка и 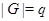 . Нетрудно показать, что
. Нетрудно показать, что  . Так как
. Так как  , имеем
, имеем  . Отсюда следует, что
. Отсюда следует, что  . Противоречие.
. Противоречие.
Пусть теперь 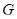 --- группа Шмидта. Поскольку
--- группа Шмидта. Поскольку  , то из свойств группы Шмидта следует
, то из свойств группы Шмидта следует  , где
, где  и
и  . Так как
. Так как 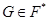 , то
, то  . Из того, что
. Из того, что  , следует
, следует  . Так как
. Так как  и
и 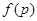 --- наследственная формация, то
--- наследственная формация, то  . Теперь из того, что
. Теперь из того, что  , где
, где  --- единственная минимальная нормальная подгруппа группы
--- единственная минимальная нормальная подгруппа группы  и
и 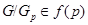 , следует что
, следует что 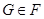 . Получили противоречие. Итак,
. Получили противоречие. Итак,  , значит,
, значит, 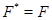 .
.
Так как  --- локальный экран формации
--- локальный экран формации 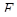 , имеем
, имеем

следовательно, 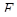 --- формация из 2).
--- формация из 2).
Пусть  . Тогда из следствия 3.2.5 следует, что
. Тогда из следствия 3.2.5 следует, что  --- сверхрадикальная формация. Теорема доказана.
--- сверхрадикальная формация. Теорема доказана.
Покажем, что в теореме 3.3.6 условие наследственной насыщенной формации  можно отбросить, в случае, когда
можно отбросить, в случае, когда 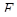 --- разрешимая формация.
--- разрешимая формация.
3.7 Лемма. Пусть 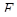 --- разрешимая нормально наследственная формация. Если
--- разрешимая нормально наследственная формация. Если  и
и  , то
, то  .
.
Доказательство. Пусть  и
и  . Если
. Если  , то утверждение леммы очевидно. Пусть
, то утверждение леммы очевидно. Пусть 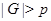 . Пусть
. Пусть  --- нормальная максимальная подгруппа группы
--- нормальная максимальная подгруппа группы 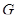 . Если
. Если  , то
, то  .
.
Пусть  . Ясно, что
. Ясно, что  . Так как
. Так как  и
и  --- нормально наследственная формация, то
--- нормально наследственная формация, то  . Индукцией по порядку группы
. Индукцией по порядку группы 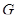 получаем, что
получаем, что  . Лемма доказана.
. Лемма доказана.
Если  --- произвольный класс групп, то через
--- произвольный класс групп, то через  обозначим наибольший по включению наследственный подкласс класса
обозначим наибольший по включению наследственный подкласс класса  . Более точно
. Более точно

3.8 Лемма. Всякая разрешимая сверхрадикальная формация является наследственной формацией.
Доказательство. Пусть 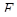 --- разрешимая сверхрадикальная формация. Как и в теореме 3.3.6 нетрудно показать, что любая разрешимая минимальная не
--- разрешимая сверхрадикальная формация. Как и в теореме 3.3.6 нетрудно показать, что любая разрешимая минимальная не 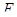 -группа является группой Шмидта, либо группой простого порядка.
-группа является группой Шмидта, либо группой простого порядка.
Покажем, что  , где
, где 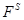 --- максимальная наследственная подформация из
--- максимальная наследственная подформация из 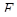 . Допустим, что множество
. Допустим, что множество 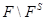 непусто и выберем в нем группу
непусто и выберем в нем группу 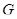 наименьшего порядка. В силу леммы 2.2.11, формация
наименьшего порядка. В силу леммы 2.2.11, формация 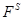 является насыщенной. Поэтому
является насыщенной. Поэтому  . Очевидно, что группа
. Очевидно, что группа 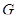 имеет единственную минимальную нормальную подгруппу
имеет единственную минимальную нормальную подгруппу  и
и  . Так как
. Так как  , то в
, то в 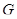 найдется минимальная не
найдется минимальная не  -группа
-группа  . Из нормальной наследственности формации
. Из нормальной наследственности формации  следует, что
следует, что  . Ясно, что
. Ясно, что  является также минимальной не
является также минимальной не  -группой.
-группой.
По условию,  --- группа Шмидта. В этом случае
--- группа Шмидта. В этом случае  , где
, где  --- нормальная силовская
--- нормальная силовская  -подгруппа, а
-подгруппа, а  --- циклическая
--- циклическая  -подгруппа группы
-подгруппа группы  ,
,  и
и  --- различные простые числа.
--- различные простые числа.
Если  , то
, то

Получили противоречие с выбором  . Остается принять, что
. Остается принять, что  . Отсюда и из
. Отсюда и из  получаем, что
получаем, что  , а значит,
, а значит, 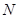 ---
---  -группа. Рассмотрим
-группа. Рассмотрим  . Тогда группу
. Тогда группу  можно представить в виде
можно представить в виде

где  --- элементарная абелева
--- элементарная абелева  -группа, а
-группа, а  . Так как
. Так как  не входит в
не входит в  , то по лемме 2.2.12
, то по лемме 2.2.12  , где
, где  --- максимальный внутренний локальный экран формации
--- максимальный внутренний локальный экран формации  . Так как
. Так как  и
и  , то
, то 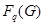 является
является  -группой. Отсюда следует, что
-группой. Отсюда следует, что  . Из нормальной наследственности формации
. Из нормальной наследственности формации  , по теореме 2.2.13, следует, что
, по теореме 2.2.13, следует, что  является нормально наследственной формацией. Тогда, по лемме 3.3.7,
является нормально наследственной формацией. Тогда, по лемме 3.3.7,  . Получили противоречие. Таким образом,
. Получили противоречие. Таким образом,  . Лемма доказана.
. Лемма доказана.
Напомним, что формация  называется формацией Шеметкова, если любая минимальная не
называется формацией Шеметкова, если любая минимальная не  -группа является либо группой Шмидта, либо группой простого порядка.
-группа является либо группой Шмидта, либо группой простого порядка.
3.9 Теорема [16-A]. Пусть  --- наследственная насыщенная формация. Тогда следующие утверждения эквивалентны:
--- наследственная насыщенная формация. Тогда следующие утверждения эквивалентны:
1)  --- формация Шеметкова;
--- формация Шеметкова;
2) формация  содержит любую группу
содержит любую группу  , где
, где  и
и 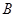 ---
---  -достижимые
-достижимые  -подгруппы из
-подгруппы из  и
и  ;
;
3)  --- сверхрадикальная формация и
--- сверхрадикальная формация и  ;
;
4) формация  такая, что для любой группы
такая, что для любой группы  и для любых ее перестановочных
и для любых ее перестановочных  -субнормальных подгрупп
-субнормальных подгрупп  и
и  подгруппа
подгруппа 
 -субнормальна в
-субнормальна в  и
и 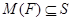 ;
;
5) формация  такая, что для любой группы
такая, что для любой группы  и для любых ее перестановочных
и для любых ее перестановочных  -достижимых подгрупп
-достижимых подгрупп  и
и  подгруппа
подгруппа 
 -достижима в
-достижима в  и
и 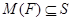 ;
;
6)  , где
, где  --- некоторые множества простых чисел и
--- некоторые множества простых чисел и 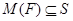 .
.
Доказательство следует из теорем 2.2.14, 2.2.15 и теоремы 3.3.6.
3.10 Теорема [3-A, 5-A]. Пусть  --- наследственная насыщенная формация такая, что
--- наследственная насыщенная формация такая, что 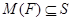 . Тогда следующие утверждения эквивалентны:
. Тогда следующие утверждения эквивалентны:
1) формация  содержит любую группу
содержит любую группу  , где
, где  и
и  ---
---  -субнормальны в G и
-субнормальны в G и 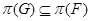 ;
;
2)  , где
, где 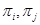 --- некоторые множества простых чисел.
--- некоторые множества простых чисел.
Доказательство. Покажем, что из 1) следует 2).
Пусть  --- формация, удовлетворяющая утверждению 1). Покажем, что она является сверхрадикальной формацией. Пусть
--- формация, удовлетворяющая утверждению 1). Покажем, что она является сверхрадикальной формацией. Пусть 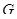 --- любая группа такая, что
--- любая группа такая, что  , где
, где  и
и 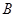 ---
---  -субнормальные подгруппы группы
-субнормальные подгруппы группы  , принадлежащие
, принадлежащие  . Пусть
. Пусть  и
и  произвольные
произвольные  -силовские подгруппы из
-силовские подгруппы из  и
и 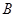 соответственно. Так как
соответственно. Так как  ,
,  и
и  --- наследственная формация, то
--- наследственная формация, то  и
и 
 -субнормальны соответственно в
-субнормальны соответственно в  и
и 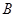 . Так как
. Так как  и
и 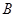
 -субнормальны в
-субнормальны в  , то по лемме 3.1.4,
, то по лемме 3.1.4,  и
и 
 -субнормальны в группе
-субнормальны в группе  . Отсюда следует, что
. Отсюда следует, что  . Следовательно,
. Следовательно,  --- сверхрадикальная
--- сверхрадикальная
|
из
5.00
|
Обсуждение в статье: Сверхрадикальные формации |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

