 |
Главная |
Критерий принадлежности факторизуемой группы классическим классам конечных групп
|
из
5.00
|
В работе [3] А.Ф. Васильевым была предложена задача об описании наследственных насыщенных формаций, замкнутых относительно произведения подгрупп  и
и  , у которых любая силовская подгруппа
, у которых любая силовская подгруппа  -субнормальна в
-субнормальна в  . В этой же работе было получено описание таких формаций в классе конечных разрешимых групп. Развитию данного направления были посвящены работы [4, 16].
. В этой же работе было получено описание таких формаций в классе конечных разрешимых групп. Развитию данного направления были посвящены работы [4, 16].
В данном разделе найдены серии наследственных насыщенных формаций, не входящих в класс конечных разрешимых групп, обладающих отмеченным выше свойством.
В теории классов групп важную роль играет класс всех  -групп (
-групп (  --- некоторое множество простых чисел), который обозначается через
--- некоторое множество простых чисел), который обозначается через  . Большинство важнейших классов групп можно построить из классов вида
. Большинство важнейших классов групп можно построить из классов вида  с помощью операций пересечения и произведения классов.
с помощью операций пересечения и произведения классов.
Напомним, что произведением классов групп  и
и  называется класс групп
называется класс групп  , который состоит из всех групп
, который состоит из всех групп 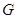 , таких, что в
, таких, что в  найдется нормальная
найдется нормальная  -подгруппа
-подгруппа  с условием
с условием  .
.
Пусть  --- множество всех натуральных чисел. Обозначим через
--- множество всех натуральных чисел. Обозначим через  некоторое подмножество из
некоторое подмножество из  . Пусть
. Пусть  ,
,  --- некоторые множества простых чисел, а
--- некоторые множества простых чисел, а  ,
,  --- классы всех
--- классы всех  -групп и
-групп и  -групп соответственно. В дальнейшем рассматриваем формации вида:
-групп соответственно. В дальнейшем рассматриваем формации вида:

Напомним, что группа  называется
называется  -замкнутой (
-замкнутой (  -нильпотентной), если ее силовская
-нильпотентной), если ее силовская  -подгруппа (силовское
-подгруппа (силовское  -дополнение) нормальна в
-дополнение) нормальна в  . Группа
. Группа  называется
называется  -разложимой, если она одновременно
-разложимой, если она одновременно  -замкнута и
-замкнута и  -нильпотентна.
-нильпотентна.
Через  обозначим дополнение к
обозначим дополнение к  во множестве всех простых чисел, если
во множестве всех простых чисел, если  , то вместо
, то вместо 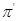 будем просто писать
будем просто писать  . Тогда
. Тогда 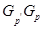 --- класс всех
--- класс всех  -нильпотентных групп,
-нильпотентных групп, 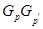 --- класс всех
--- класс всех  -замкнутых групп,
-замкнутых групп,  --- класс всех
--- класс всех  -разложимых групп,
-разложимых групп,  --- класс всех нильпотентных групп, где
--- класс всех нильпотентных групп, где  пробегает все простые числа.
пробегает все простые числа.
Группа  называется
называется  -нильпотентной (
-нильпотентной (  -разложимой), если она
-разложимой), если она  -нильпотентна (
-нильпотентна (  -разложима) для любого простого числа
-разложима) для любого простого числа  из
из  . Классы всех
. Классы всех  -нильпотентных (
-нильпотентных (  -разложимых) групп можно записать в виде
-разложимых) групп можно записать в виде

Группа  называется
называется  -замкнутой, если она имеет нормальную
-замкнутой, если она имеет нормальную  -холлову подгруппу. Тогда
-холлову подгруппу. Тогда 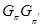 --- класс всех
--- класс всех  -замкнутых групп.
-замкнутых групп.
2.1 Лемма. Пусть  --- наследственная формация. Если
--- наследственная формация. Если 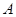 ---
---  -субнормальная
-субнормальная  -подгруппа группы
-подгруппа группы  , то композиционные факторы группы
, то композиционные факторы группы  содержатся среди композиционных факторов групп из
содержатся среди композиционных факторов групп из  .
.
Доказательство. Если  , то лемма верна. Пусть
, то лемма верна. Пусть  . Тогда
. Тогда 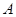 содержится в
содержится в  -нормальной максимальной подгруппе
-нормальной максимальной подгруппе 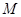 группы
группы  . По индукции,
. По индукции, 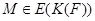 . Так как
. Так как  , то
, то  . Отсюда, и из
. Отсюда, и из  , получаем
, получаем  . Лемма доказана.
. Лемма доказана.
2.2 Лемма. Пусть  --- наследственная формация,
--- наследственная формация, 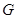 --- класс всех групп. Тогда формация
--- класс всех групп. Тогда формация  совпадает с формацией
совпадает с формацией  .
.
Доказательство леммы осуществляется непосредственной проверкой.
2.3 Теорема [10-A, 13-A]. Пусть  --- наследственная формация. Тогда всякая формация
--- наследственная формация. Тогда всякая формация  , представимая в виде
, представимая в виде  , содержит любую группу
, содержит любую группу  , у которой
, у которой 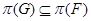 и силовские подгруппы из подгрупп
и силовские подгруппы из подгрупп 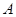 и
и 
 -субнормальны в
-субнормальны в 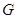 .
.
Доказательство. Пусть  --- формация указанного вида и
--- формация указанного вида и  --- такая группа, что
--- такая группа, что  , где
, где  и любая силовская подгруппа из
и любая силовская подгруппа из 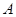 и
и 
 -субнормальна в
-субнормальна в 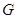 . Индукцией по порядку
. Индукцией по порядку  докажем, что
докажем, что  . Рассмотрим сначала случай, когда
. Рассмотрим сначала случай, когда  --- класс всех групп.
--- класс всех групп.
Пусть  --- минимальная нормальная подгруппа из
--- минимальная нормальная подгруппа из  . Ясно, что любая силовская подгруппа из
. Ясно, что любая силовская подгруппа из  и
и  имеет вид
имеет вид  ,
, 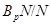 , где
, где  и
и  --- силовские подгруппы из
--- силовские подгруппы из  и
и  соответственно. Согласно лемме 3.1.5,
соответственно. Согласно лемме 3.1.5, 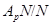 и
и 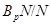 ---
---  -субнормальные подгруппы фактор-группы
-субнормальные подгруппы фактор-группы  . По индукции,
. По индукции,  . Так как
. Так как  --- формация, то отсюда следует, что
--- формация, то отсюда следует, что  имеет единственную минимальную нормальную подгруппу
имеет единственную минимальную нормальную подгруппу  . Очевидно, что
. Очевидно, что 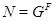 . Так как
. Так как  --- насыщенная формация, то нетрудно показать, что
--- насыщенная формация, то нетрудно показать, что  .
.
Пусть  --- силовская подгруппа из
--- силовская подгруппа из  . Покажем, что
. Покажем, что  .
.
Пусть  --- абелева группа. Так как
--- абелева группа. Так как  ---
---  -субнормальная подгруппа группы
-субнормальная подгруппа группы  , то, согласно теореме 2.2.8,
, то, согласно теореме 2.2.8,  .
.
Пусть  --- неабелева группа. В этом случае
--- неабелева группа. В этом случае  есть прямое произведение изоморфных неабелевых простых групп и
есть прямое произведение изоморфных неабелевых простых групп и  .
.
Рассмотрим подгруппу 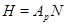 . Согласно лемме 3.1.5,
. Согласно лемме 3.1.5,  ---
---  -субнормальная подгруппа группы
-субнормальная подгруппа группы 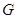 . Пусть
. Пусть 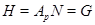 . Так как
. Так как 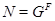 и
и  --- собственная
--- собственная  -субнормальная подгруппа группы
-субнормальная подгруппа группы  , то равенство
, то равенство 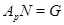 невозможно. Итак,
невозможно. Итак, 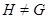 .
.
Так как  и
и  --- насыщенная формация, то
--- насыщенная формация, то 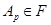 . Отсюда следует, что
. Отсюда следует, что
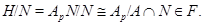
А это значит, что  . Если
. Если  , то
, то  . Последнее равенство невозможно, так как
. Последнее равенство невозможно, так как  согласно лемме 3.1.4 --- собственная
согласно лемме 3.1.4 --- собственная  -субнормальная подгруппа
-субнормальная подгруппа  .
.
Итак,  --- собственная подгруппа
--- собственная подгруппа  . Если
. Если 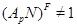 , то
, то

Так как  и
и  --- наследственная формация, то
--- наследственная формация, то  . Но тогда нетрудно заметить, что
. Но тогда нетрудно заметить, что  .
.
Так как  , то согласно лемме 3.1.4,
, то согласно лемме 3.1.4,  ---
---  -субнормальная подгруппа. Так как
-субнормальная подгруппа. Так как  и
и  --- наследственная формация, то любая силовская подгруппа
--- наследственная формация, то любая силовская подгруппа 
 -субнормальна в
-субнормальна в  . Согласно лемме 3.1.4,
. Согласно лемме 3.1.4,  ---
---  -субнормальная подгруппа группы
-субнормальная подгруппа группы  . По индукции,
. По индукции,  . Отсюда следует, что
. Отсюда следует, что  для любой
для любой  .
.
Аналогичным образом доказывается, что  для любой
для любой  , где
, где  --- любая силовская подгруппа из
--- любая силовская подгруппа из  . Из того, что
. Из того, что  , следует
, следует  .
.
Рассмотрим два случая:  и
и  .
.
Пусть  . Покажем, что
. Покажем, что  .
.
Если  --- абелева, то
--- абелева, то  --- примарная
--- примарная  -группа, где
-группа, где  . Отсюда следует, что
. Отсюда следует, что  .
.
Если  --- неабелева, то
--- неабелева, то  есть прямое произведение изоморфных неабелевых простых групп.
есть прямое произведение изоморфных неабелевых простых групп.
Так как  --- нормальная подгруппа из
--- нормальная подгруппа из  , то
, то
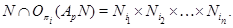
Так как 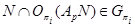 , то очевидно, что
, то очевидно, что  . Так как
. Так как  , то
, то  для любой
для любой  . Следовательно,
. Следовательно,  .
.
Пусть теперь  . Если
. Если  --- неабелева, то
--- неабелева, то  . Тогда
. Тогда  . Отсюда следует, что
. Отсюда следует, что  . А это значит, что
. А это значит, что  . Отсюда следует, что
. Отсюда следует, что  , где
, где  --- любое простое число из
--- любое простое число из  .
.
Рассмотрим подгруппу  , где
, где  --- любая силовская подгруппа из
--- любая силовская подгруппа из  .
.
Если  , то, как и выше, получаем, что
, то, как и выше, получаем, что  .
.
Если 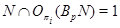 , то, как и выше, получаем, что
, то, как и выше, получаем, что  . Отсюда следует, что
. Отсюда следует, что  , где
, где  --- любое простое число из
--- любое простое число из  . Согласно лемме 2.2.9, любая силовская подгруппа
. Согласно лемме 2.2.9, любая силовская подгруппа  группы
группы  есть
есть  , где
, где  --- силовские подгруппы из
--- силовские подгруппы из  и
и  соответственно. Отсюда следует, что любое простое число
соответственно. Отсюда следует, что любое простое число  из
из  принадлежит
принадлежит  . Следовательно,
. Следовательно,  . А это значит, что
. А это значит, что  .
.
Пусть  --- абелева группа, то
--- абелева группа, то  . Но тогда
. Но тогда  .
.
Ввиду  , получаем, что
, получаем, что  для любой
для любой 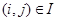 . А это значит, что
. А это значит, что  .
.
Пусть теперь  --- произвольная наследственная формация и
--- произвольная наследственная формация и  . По лемме 3.2.1, композиционные факторы группы
. По лемме 3.2.1, композиционные факторы группы  содержатся среди композиционных факторов групп из
содержатся среди композиционных факторов групп из  . Это значит, что
. Это значит, что  принадлежит
принадлежит  .
.
Пусть  . Так как
. Так как 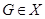 , то ввиду леммы 3.2.2, силовские подгруппы из
, то ввиду леммы 3.2.2, силовские подгруппы из  и
и 
 -субнормальны в
-субнормальны в  . По доказанному,
. По доказанному,  . Так как
. Так как  , то, по лемме 3.2.2,
, то, по лемме 3.2.2,  . Теорема доказана.
. Теорема доказана.
2.4 Следствие (В.Н. Семенчук, Л.А. Шеметков [33]). Пусть  --- наследственная формация. Тогда всякая формация вида
--- наследственная формация. Тогда всякая формация вида  является сверхрадикальной.
является сверхрадикальной.
Доказательство. Пусть  , где
, где  и
и  ---
---  -субнормальные
-субнормальные  -подгруппы группы
-подгруппы группы  . Так как
. Так как  --- наследственная формация, то согласно лемме 3.1.4, любая силовская подгруппа из
--- наследственная формация, то согласно лемме 3.1.4, любая силовская подгруппа из  (из
(из  )
)  -субнормальна в
-субнормальна в  (соответственно в
(соответственно в  ). Отсюда, согласно лемме 3.1.4, любая силовская подгруппа из
). Отсюда, согласно лемме 3.1.4, любая силовская подгруппа из  и из
и из 
 -субнормальна в
-субнормальна в 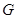 . Теперь требуемый результат следует из теоремы 3.2.3.
. Теперь требуемый результат следует из теоремы 3.2.3.
2.5 Следствие (В.Н. Семенчук, Л.А. Шеметков [33]). Формация вида  является сверхрадикальной.
является сверхрадикальной.
2.6 Следствие. Пусть  --- формация всех
--- формация всех  -нильпотентных групп. Тогда
-нильпотентных групп. Тогда  содержит любую группу
содержит любую группу  , где
, где  и
и  ---
---  -субнормальные подгруппы группы
-субнормальные подгруппы группы  , принадлежащие
, принадлежащие  .
.
2.7 Следствие. Пусть  --- формация всех
--- формация всех  -замкнутых групп. Тогда
-замкнутых групп. Тогда  содержит любую группу
содержит любую группу  , где
, где  и
и  ---
---  -субнормальные подгруппы группы
-субнормальные подгруппы группы  , принадлежащие
, принадлежащие  .
.
2.8 Следствие. Пусть  --- формация всех
--- формация всех  -разложимых групп. Тогда
-разложимых групп. Тогда  содержит любую группу
содержит любую группу  , где
, где  и
и  ---
---  -субнормальные подгруппы группы
-субнормальные подгруппы группы  , принадлежащие
, принадлежащие  .
.
2.9 Следствие [10-A, 13-A]. Пусть  . Тогда формация
. Тогда формация  содержит любую группу
содержит любую группу  , у которой
, у которой 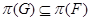 и силовские подгруппы из подгрупп
и силовские подгруппы из подгрупп 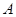 и
и 
 -субнормальны в
-субнормальны в  .
.
2.10 Следствие [10-A, 13-A]. Пусть  --- формация всех
--- формация всех  -нильпо- тентных групп. Тогда
-нильпо- тентных групп. Тогда  содержит любую группу
содержит любую группу  , у которой силовские подгруппы из подгрупп
, у которой силовские подгруппы из подгрупп  и
и 
 -субнормальны в
-субнормальны в  .
.
2.11 Следствие [10-A, 13-A]. Пусть  --- формация всех
--- формация всех  -замкнутых групп. Тогда
-замкнутых групп. Тогда  содержит любую группу
содержит любую группу  , у которой силовские подгруппы из подгрупп
, у которой силовские подгруппы из подгрупп  и
и 
 -субнормальны в
-субнормальны в  .
.
2.12 Следствие [10-A, 13-A]. Пусть  --- формация всех
--- формация всех  -разложимых групп. Тогда
-разложимых групп. Тогда  содержит любую группу
содержит любую группу  , у которой силовские подгруппы из подгрупп
, у которой силовские подгруппы из подгрупп  и
и 
 -субнормальны в
-субнормальны в  .
.
2.13 Лемма. Пусть  --- непустая наследственная формация. Пусть все композиционные факторы группы
--- непустая наследственная формация. Пусть все композиционные факторы группы  принадлежат
принадлежат  . Тогда следующие утверждения эквивалентны:
. Тогда следующие утверждения эквивалентны:
1)  ---
---  -субнормальная подгруппа группы
-субнормальная подгруппа группы  ;
;
2)  ---
---  -достижимая подгруппа группы
-достижимая подгруппа группы  .
.
Доказательство. Пусть  ---
---  -субнормальная подгруппа группы
-субнормальная подгруппа группы  . Тогда, по определению,
. Тогда, по определению,  ---
---  -достижимая подгруппа группы
-достижимая подгруппа группы  .
.
Пусть  ---
---  -достижимая подгруппа группы
-достижимая подгруппа группы 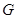 . Тогда существует цепь
. Тогда существует цепь
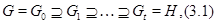
в которой для любого  либо
либо  нормальна в
нормальна в  , либо
, либо  .
.
Пусть  . Уплотним участок от
. Уплотним участок от 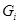 до
до  цепи
цепи  до максимальной
до максимальной 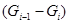 -цепи.
-цепи.
Ввиду утверждения 1) леммы 3.1.4, все подгруппы  , содержащие
, содержащие 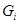 ,
,  -субнормальны в
-субнормальны в  . Пусть теперь
. Пусть теперь 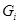 нормальна в
нормальна в  . Можно считать, что
. Можно считать, что  --- максимальная нормальная подгруппа
--- максимальная нормальная подгруппа  (в противном случае уплотняем участок от
(в противном случае уплотняем участок от 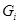 до
до  до композиционной
до композиционной  -цепи). Ввиду условия леммы
-цепи). Ввиду условия леммы  , т. е.
, т. е.  . Пришли к рассматриваемому выше случаю. Теперь, ввиду утверждения 1) леммы 3.1.4, подгруппа
. Пришли к рассматриваемому выше случаю. Теперь, ввиду утверждения 1) леммы 3.1.4, подгруппа 
 -субнормальна в
-субнормальна в  . Лемма доказана.
. Лемма доказана.
2.14 Лемма. Пусть  --- наследственная насыщенная формация. Тогда следующие утверждения эквивалентны:
--- наследственная насыщенная формация. Тогда следующие утверждения эквивалентны:
1) любая группа  , где
, где  и любые силовские подгруппы из подгрупп
и любые силовские подгруппы из подгрупп  и
и 
 -субнормальны в
-субнормальны в  , принадлежит
, принадлежит  ;
;
2) любая группа  , где
, где  и любые силовские подгруппы из подгрупп
и любые силовские подгруппы из подгрупп  и
и 
 -достижимы в
-достижимы в  , принадлежит
, принадлежит  .
.
Доказательство. Покажем, что из 1) следует 2). Доказательство проведем индукцией по порядку группы  .
.
Пусть  --- минимальная нормальная подгруппа группы
--- минимальная нормальная подгруппа группы 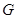 . Очевидно, что
. Очевидно, что  . Пусть
. Пусть  --- произвольная
--- произвольная  -силовская подгруппа из
-силовская подгруппа из 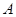 . Ясно, что
. Ясно, что  ---
---  -силовская подгруппа из
-силовская подгруппа из  . По лемме 3.1.5,
. По лемме 3.1.5,  ---
---  -достижимая подгруппа группы
-достижимая подгруппа группы  . Аналогичным образом доказыватся, что любая силовская подгруппа из
. Аналогичным образом доказыватся, что любая силовская подгруппа из 
 -достижима в
-достижима в  . Так как
. Так как  , то по индукции,
, то по индукции,  . Предположим, что
. Предположим, что  и
и 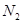 --- две различные минимальные нормальные подгруппы группы
--- две различные минимальные нормальные подгруппы группы  . Выше показано, что
. Выше показано, что  ,
,  . Так как
. Так как  --- формация, то
--- формация, то  . Итак,
. Итак,  имеет единственную минимальную нормальную подгруппу
имеет единственную минимальную нормальную подгруппу  .
.
Покажем, что  . Предположим противное. Тогда, как и выше, с учетом индукции можно показать, что
. Предположим противное. Тогда, как и выше, с учетом индукции можно показать, что  . Так как
. Так как  --- наследственная формация, то
--- наследственная формация, то  . Итак,
. Итак,  .
.
Рассмотрим следующие два случая.
1) Пусть  --- абелева, тогда
--- абелева, тогда  --- примарная группа. Так как
--- примарная группа. Так как  --- насыщенная формация и
--- насыщенная формация и 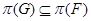 , то
, то  . Как и выше, с учетом индукции можно показать, что
. Как и выше, с учетом индукции можно показать, что  . Теперь, с учетом леммы 3.2.13 и условия следует, что
. Теперь, с учетом леммы 3.2.13 и условия следует, что  .
.
2) Пусть  --- неабелева группа. В этом случае
--- неабелева группа. В этом случае

есть прямое произведение изоморфных неабелевых простых групп и  .
.
Рассмотрим подгруппу  . Согласно лемме 3.1.5,
. Согласно лемме 3.1.5,  ---
---  -субнормальная подгруппа группы
-субнормальная подгруппа группы 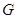 . Пусть
. Пусть 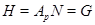 . Так как
. Так как  и
и  --- собственная
--- собственная  -субнормальная подгруппа группы
-субнормальная подгруппа группы  , то равенство
, то равенство  невозможно. Итак,
невозможно. Итак, 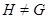 .
.
Так как  и
и  --- насыщенная формация, то
--- насыщенная формация, то  . Отсюда следует, что
. Отсюда следует, что

А это значит, что  . Если
. Если  , то
, то  . Последнее равенство невозможно, так как
. Последнее равенство невозможно, так как  , согласно лемме 3.1.4, собственная
, согласно лемме 3.1.4, собственная  -субнормальная подгруппа
-субнормальная подгруппа  .
.
Итак,  --- собственная подгруппа
--- собственная подгруппа  . Если
. Если  , то
, то
|
из
5.00
|
Обсуждение в статье: Критерий принадлежности факторизуемой группы классическим классам конечных групп |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

