Зависимость между групповой скоростью волн и скоростью их распространения.

Скорость, обозначаемая ранее буквой с и называемая скоростью распространения волны, - есть ни что иное, как фазовая скорость (т.е. скорость перемещения гребней волн). От неё следует отличать скорость распространения группы волн, называемую групповой скоростью (далее она будет иметь обозначение с*).

Понять различие между ними проще всего на примере картины, возникающей в результате наложения двух волн, имеющих разные амплитуды, но немного отличающиеся своей длиной. Пусть имеется синусоидальная волна

y = A sin (μx - νt),

где А есть амплитуда, t – время, а μ и ν – некоторые коэффициенты.

При изменении x на  или t на  синус принимает прежнее значение (т. к. sin (φ+2π) = sin (φ) по формулам приведения. Следовательно, величина

 - это длина волны, (4.4)

а величина 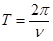 - период колебаний. Если (4.5)

μx – νt = const, т. е. если x = const + ,

то аргумент синуса не зависит от времени, поэтому не зависит от времени и ордината y. Это означает, что вся волна, не изменяя своей формы, перемещается вправо со скоростью . (4.6)

Пусть на эту волну накладывается вторая волна

y′ = A sin (μ′x - ν′t),

т. е. волна с той же амплитудой А, но с несколько иными значениями μ и ν. Результирующим движением будет

 y + y′ = A[sin (μx - νt)+ sin (μ′x - ν′t)]. (4.7)

В тех точках оси x, в которых фазы обоих колебаний совпадают, амплитуда равна 2A, в тех же точках, в которых фазы обоих колебаний противоположны, амплитуда равна нулю. Такое явление называется биением. После применения к 4.7 правила сложения синусов, получается выражение

 y + y′ = 2A cos sin .

В этом равенстве член sin  представляет собой волну, для которой коэффициенты при x и t равны средним значениям от μ и μ′ и соответственно от ν и ν′.

Множитель 2A cos , в свою очередь, можно рассматривать как переменную амплитуду (при малых различиях параметров этот множитель изменяется очень медленно).

Группа волн кончается в той точке, где косинус делается равным нулю. Скорость перемещения этой точки (она и называется групповой скоростью) на основании выведенного соотношения 4.6 равна

. (4.8)

Для длинных групп, т. е. для медленных биений (см. пункт 4.1 – зависимость длины волны от скорости), с достаточной точностью можно принять, что

.

Соотношения между групповой скоростью и скоростью распространения волны определяются следующим образом:

1) для гравитационных волн:

Из формулы 4.1 : , но, согласно равенству 4.5, , следовательно .

С другой стороны, после подстановки в формулу 4.2 значения λ из 4.4, получается:

, поэтому .

Дифференцирование по μ с учётом равенства 4.8 даёт результат:

.

2) для капиллярных волн:

Из формулы 4.5 : , но, согласно равенству 4.4, .

Дифференцирование этого выражения по μ с учётом 4.8 и выражения скорости для предельного случая очень короткой капиллярной волны  (см. формулу 4.3 и пункт 4.1) даёт результат:

.

Таким образом, группы гравитационных волн распространяются со скоростью с^*, равной половине фазовой скорости, иными словами, гребни в группе волн перемещаются со скоростью, в два раза большей, чем сама группа волн; на заднем конце группы всё время возникают новые волны, а на переднем конце группы они исчезают. Это явление очень легко наблюдать на волнах, вызванных падением камня в неподвижную воду.

Групповая скорость капиллярных волн больше фазовой скорости, а именно, в предельном случае очень малых волн, в 1,5 раза. Следовательно, если очаг возмущения движется с постоянной скоростью, то группы волн его опережают.