Булевы функции двух переменных

Введение

 

Тема контрольной работы «Математическая логика».

БУЛЬ или БУЛ, а также БУУЛ, Джордж (1815-1864) – английский математик, который считается основоположником математической логики.

Математическая логика – это раздел математики, посвященный анализу методов рассуждений, при этом в первую очередь исследуются формы рассуждений, а не их содержание, т.е. исследуется формализация рассуждений.

Формализация рассуждений восходит к Аристотелю. Современный вид аристотелева (формальная) логика приобрела во второй половине XIX века в сочинении Джорджа Буля “Законы мысли”.

Интенсивно математическая логика начала развиваться в 50-е годы XX века в связи с бурным развитием цифровой техники.

Элементы математической логика

 

Основными разделами математической логики являются исчисление высказываний и исчисление предикатов.

Высказывание – есть предложение, которое может быть либо истинно, либо ложно.

Исчисление высказываний – вступительный раздел математической логики, в котором рассматриваются логические операции над высказываниями.

Предикат – логическая функция от п переменных, которая принимает значения истинности или ложности.

Исчисление предикатов – раздел математической логики, объектом которого является дальнейшее изучение и обобщение исчисления высказываний.

Теория булевых алгебр (булевых функций) положена в основу точных методов анализа и синтеза в теории переключательных схем при проектировании компьютерных систем.

 

Основные понятия алгебры логики

 

Алгебра логики – раздел математической логики, изучающий логические операции над высказываниями.

В алгебре логики интересуются лишь истинностным значением высказываний. Истинностные значения принято обозначать:

1 (истина) 0 (ложь).

Каждой логической операции соответствует функция, принимающая значения 1 или 0, аргументы которой также принимают значения 1 или 0.

Такие функции называются логическими или булевыми, или функциями алгебры логики (ФАЛ). При этом логическая (булева) переменная x может принимать только два значения: .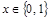

Таким образом, 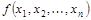 - логическая функция, у которой логи-ческие переменные  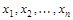являются высказываниями. Тогда сама логическая функция  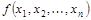является сложным высказыванием.

В этом случае алгебру логики можно определить, как совокупность множества логических функций с заданными в нем всевозможными логическими операциями. Таким логическим операциям, как конъюнкция (читается И), дизъюнкция (ИЛИ), импликация, эквивалентность, отрицание (НЕ), соответствуют логические функции, для которых приняты обозначения 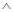(&, ·), 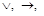~, – ( 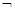), и имеет место таблица истинности:

 

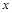
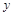
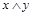
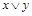
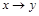
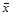
						x~y
0	0	0	0	1	1	1
0	1	0	1	1	1	0
1	0	0	1	0	0	0
1	1	1	1	1	0	1

 

Это табличный способ задания ФАЛ. Наряду с ними применяется задание функций с помощью формул в языке, содержащем переменные x , y , …, z (возможно индексированные) и символы некоторых конкретных функций – аналитический способ задания ФАЛ.

Наиболее употребительным является язык,содержащий логические символы 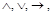 ~, –. Формулы этого языка определяются следующим образом:

1) все переменные есть формулы;

2) если P и Q – формулы, то 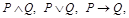 P ~ Q,  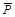- фор-мулы.

Например, выражение 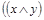~ 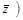- формула. Если переменным x , y , z придать значения из двоичного набора 0, 1 и провести вычисления в соответствии с операциями, указанными в формуле, то получим значение 0 или 1.

Говорят, что формула реализует функцию. Так формула 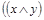~ 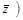реализует функцию h(x , y , z):

x	y	z	h(x, y, z)
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	0

 

Пусть P и Q – формулы, которые реализуют функции f (x₁, x₂, …, x_n) и g (x₁, x₂, …, x_n). Формулы равны: P = Q, если функции f и g совпадают, т.е. совпадают их таблицы истинности. Алгебра, основным множеством которой является все множество логических функций, а операциями – дизъюнкция, конъюнкция и отрицание, называется булевой алгеброй логических функций.

Приведем законы и тождества, определяющие операции 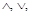– и их связь с операциями , ~:

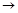1. Идемпотентность конъюнкции и дизъюнкции:

 

.

 

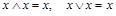2. Коммутативность конъюнкции и дизъюнкции:

 

.

 

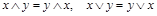3. Ассоциативность конъюнкции и дизъюнкции:

 

.

 

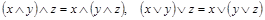4. Дистрибутивность конъюнкции относительно дизъюнкции и дизъюнкции относительно конъюнкции:

.

 

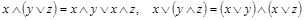5. Двойное отрицание:

.

 

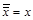6. Законы де Моргана:

 

= , = .

 

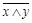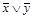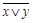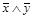7. Склеивание:

 

.

 

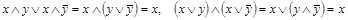8. Поглощение

 

.

 

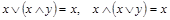9. Действия с константами 0 и 1:

 

.

 

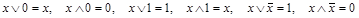10. Законы Блейка-Порецкого:

 

.

 

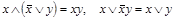11. Связь импликации 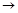 с отрицанием – и дизъюнкцией :

 

.

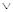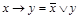12. Связь эквивалентности ~ с дизъюнкцией 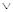, конъюнкцией  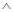и отрицанием:

 

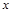~ y = .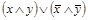

 

Всякая функция алгебры логики может быть реализована некоторой формулой языка с символами ~, –.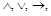

 

1.2 Дизъюнктивные и конъюнктивные нормальные формы (ДНФ и КНФ)

 

ДНФ и КНФ играют особую роль в алгебре логики и ее приложениях. Введем обозначение:

 

 

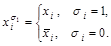
Так определенная переменная или ее отрицание называется первичным термом.

Формула вида 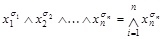, где 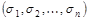- двоичный набор, а среди переменных нет одинаковых, называется элементарной конъюнкцией.

Всякая дизъюнкция элементарных конъюнкций называется дизъюнктивной нормальной формой (ДНФ):

 

.

 

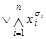Формула вида 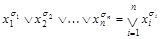 называется элементарной дизъюнкцией.

Всякая конъюнкция элементарных дизъюнкций называется конъюктивной нормальной формой (КНФ):

 

.

 

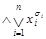Пример.

Привести формулу 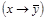~z к ДНФ и КНФ.

1) Приведем формулу к ДНФ (последовательно: на основании определений операций импликации и эквивалентности, законов де Моргана и дистрибутивности):

 

~ ~ (( ) =

.

 

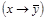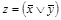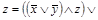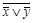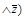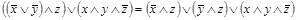2) Применив закон дистрибутивности к последнему выражению, получим КНФ:

 

 

 

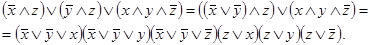
Совершенной ДНФ (СДНФ) называется ДНФ, в которой нет равных элементарных конъюнкций и все элементарные конъюнкции содержат одни и те же переменные, причем каждую переменную – только один раз (включая вхождения под знаком отрицания).

Совершенная КНФ (СКНФ) определяется как такая КНФ, в которой нет одинаковых сомножителей; все сомножители содержат одни и те же переменные, причем каждую переменную – только один раз.

Для каждой ФАЛ 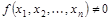 можно построить реализующую ее СДНФ:

,

 

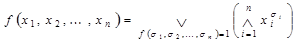где дизъюнкция берется по тем двоичным наборам, на которых f = 1.

Каждая функция алгебры логики 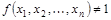 реализуется следующей СКНФ:

 

 

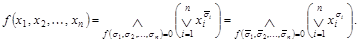
Пример.

Функция h(x , y , z), рассмотренная ранее, имеет следующую СДНФ (выписывается по единичным значениям) и СКНФ (выписывается по нулевым значениям):

 

1

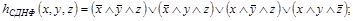
0

;

 

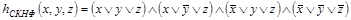x	y	z	h(x,y,z)
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	0

Пример.

Построить СДНФ и СКНФ будевой функции f(x₁, x₂, x₃), заданной таблицей истинности

 

x1	x2	x3	f(x1,x2,x3)	x1	x2	x3	f(x1,x2,x3)
0	0	0	1	1	0	0	0
0	0	1	0	1	0	1	1
0	1	0	1	1	1	0	0
0	1	1	0	1	1	1	1

 

.

 

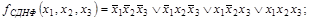
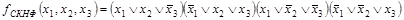Разложение булевой функции 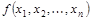 по k переменным x₁, x₂,…, x_k называется разложением Шеннона.

 

Теорема Шеннона

 

Любая булева функция 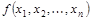 представима в виде разложе-ния Шеннона:

 

 

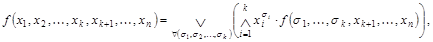
где 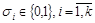,  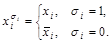- первичные термы.

Пример.

Пусть п = 4, k = 2. Тогда разложение Шеннона будет иметь вид

 

 

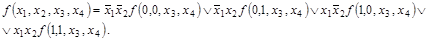
Следствие.

Предельное разложение Шеннона (k = n) булевой функции 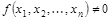 имеет вид

 

.

 

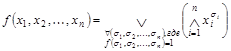Предельное разложение Шеннона булевой функции 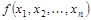 является ее СДНФ.

В алгебре логики справедлив принцип двойственности. Согласно этому принципу, будем иметь следующие двойственные разложения Шеннона булевой функции :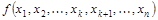

по k переменным

 

 

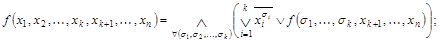
двойственное предельное разложение

 

.

 

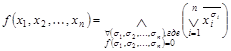Двойственное предельное разложение Шеннона булевой функции 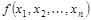 является ее СКНФ.

Булевы функции двух переменных

Рассмотрим простой бинарный элемент – выключатель, который имеет два состояния. Если данный выключатель контролируется входной переменной х,то говорят, что он выключен (открыт) при х = 0 и включен (закрыт) при х = 1, как показано на рис. 1:

 

х = 0 х = 1

Рис. 1 - Два состояния выключателя

 

Будем использовать следующее графическое обозначение для представления таких выключателей:

 

х

Рис. 2 - Графическое обозначение выключателя

 

Рассмотрим соединения лампы с источником питания, представленные следующими схемами:

 

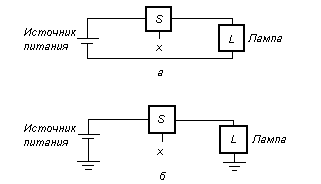
Рис. 3 - Лампа, управляемая выключателем: а – простое соединение с батареей; б – использование заземления, как обратной связи

Используя условное обозначение L , можно описать состояние лампы как функции входной переменной. Если лампа светится, то L = 1. Если лампа не светится, то L = 0. Поскольку L = 1 при х = 1, L = 0 при х = 0, то можно говорить, что L(х) = х – логическая функция, х – логическая переменная. Это простое логическое выражение описывает выход как функцию от входа.