Теорема Поста – Яблонского (критерий функциональной полноты)

 

Для того, чтобы система ФАЛ  была полной необходимо и достаточно, чтобы она содержала функцию:

1) не сохраняющую ноль;

2) не сохраняющую единицу;

3) нелинейную;

4) немонотонную;

5) несамодвойственную.

Примерами функционально полных систем являются, например, системы:

 

.

 

Все названные выше классы функций обладают свойством: любая ФАЛ, полученная с помощью операции суперпозиции и подстановки из функций одного класса, обязательно будет принадлежать этому же классу.

Полная система ФАЛ называется базисом,если теряется полнота Ф при удалении хотя бы одной функции системы.

К базису относятся системы функций:

базис 1: ;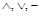

базис 2: ;

базис 3: ;

базис 4: функция Шеффера: x₁ | x₂;

базис 5: функция Пирса (Вебба): x₁ ↓ x₂.

Базис 1 – избыточный, базисы 4 и 5 – минимальные (удаление хотя бы одной функции превращает систему ФАЛ в неполную).

При исследовании полноты систем функций удобно пользоваться таблицей, которую называют критериальной. Эта таблица имеет пять столбцов, каждый из которых соответствует одному из пяти классов, а строки таблицы соответствуют функциям исследуемой системы. На пересечении строки таблицы, соответствующей функции f, и столбца, соответствующего классу К, ставится знак плюс, если функция , и минус, если . Система функций полна тогда и только тогда, когда в каждом столбце содержится хотя бы один знак минус.

Пример.

Является ли система булевых функций полной? Если является, то выписать все возможные базисы.

Рассмотрим функцию .

1. Исследуем ее принадлежность к классу К₀:

 

.

 

Следовательно, .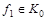

2. Исследуем принадлежность функции к классу К₁:

 

.

 

Следовательно, .

3. Установим, является ли функция f₁ линейной. Используем метод неопределенных коэффициентов. Предположим, что функция линейная и, следовательно, представима в виде полинома Жегалкина первой степени:

 

.

 

Найдем коэффициенты , исходя из предположения линейности этой функции. Зафиксируем набор 000:

 

, , .

 

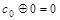Следовательно, .

Зафиксируем набор 100:

 

,

,

.

Следовательно, .

Фиксируем набор 010:

 

,

 

 

Фиксируем набор 001:

 

.

 

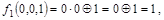
Следовательно, функция (по нашему предположению) может быть представлена полиномом первой степени вида:

 

.

 

Если функция линейная, то полученный полином, путем тождественных преобразований, должен привестись к виду заданной функции. Ясно, что полученный полином не приводится к исходной функции. Следовательно, .

4. Исследуем заданную функцию на самодвойственность.

Функция самодвойственная, если на любой паре противоположных наборов (наборов, сумма десятичных эквивалентов которых равна , где п – количество переменных функции) функция принимает противоположные значения.

Построим таблицу: ; вычислим значения функции на оставшихся наборах:

 

:

(000) 0	(001) 1	(010) 2	(011) 3	(100) 4	(101) 5	(110) 6	(111) 7
0	1	0	1	0	1	1	0

 

На наборах 0 и 7, 1 и 6 функция принимает одинаковые значения. Следовательно .

5. Проверим принадлежность заданной функции f₁ классу монотонных функций. Из таблицы видно: 001< 010, но 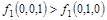. Следовательно, функция .

Рассмотрим функцию .

1. Принадлежность функции классу К₀:

 

.

 

Следовательно, .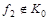

2. Принадлежность функции классу К₁:

 

.

 

Следовательно, .

3. Принадлежность функции классу К _л.

Предполагаем, что

 

.

 

Фиксируем набор 0000:

 

,

, .

Фиксируем набор 1000:

 

,

.

 

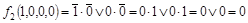Фиксируем набор 0100:

 

,

.

 

Фиксируем набор 0010:

 

,

.

 

Фиксируем набор 0001:

 

.

.

 

Окончательно получаем

 

.

 

Это равенство на других 11 наборах не выполняется. Действительно, для набора 1111 имеем

 

, , т.е. .

Следовательно, .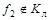

 

4. Принадлежность функции классу самодвойственных функций.

Строим таблицу:

 

0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
1	0	1	0	1	1	1	0	0	0	0	0	1	1	0	0

 

Из таблицы видно, что на наборах 1 и 14, 2 и 13, 7 и 8 функция принимает одинаковые значения. Следовательно, .

5. Принадлежность функции классу монотонных функций.

Из таблицы видно, что 1000>0000, а . Следовательно, .

Строим критериальную таблицу:

 

	К 0	К 1	К л	К с	К м
f 1	+	-	-	-	-
f 2	-	-	-	-	-

 

В таблице в каждом столбце стоит хотя бы один минус. Следовательно, система булевых функций является полной.

 

 

Найдем все возможные базисы. По критериальной таблице составим к.н.ф. К, в которой элементарные дизъюнкции соответствуют столбцам таблицы и включают в качестве слагаемых символы тех функций, которые не входят в класс, соответствующий столбцу. В данном случае имеем

 

.

Используя законы и свойства дизъюнкции и конъюнкции, приведем к.н.ф. К к д.н.ф. D, в которой упрощение 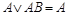 невозможно. В нашем случае получим

 

.

 

По полученной д.н.ф. D выпишем подмножества функций, соответствующие слагаемым д.н.ф. D. Это и будут искомые базисы. В нашем случае имеется два базиса:

 

.

 

Минимальная форма представления ФАЛ содержит минимальное количество термов и переменных в термах (т.е. не допускает никаких упрощений).

Пример.

 

,

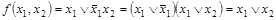 - минимальная форма.