 |
Главная |
Обусловленность вычислительной задачи
|
из
5.00
|
Под обусловленностью вычислительной задачи понимают чувствительность ее решения к малым погрешностям ИД. Задача хорошо обусловлена, если малым погрешностям ИД отвечают малые погрешности решения, и плохо обусловленной, если возможны сильные изменения решения. Количественной мерой степени обусловленности задачи является число обусловленности. Сформулируем эти положения точнее: если существует такое положительное число  , что имеет место неравенство
, что имеет место неравенство  , то число
, то число  называетсячислом обусловленности задачи (абсолютным числом обусловленности).
называетсячислом обусловленности задачи (абсолютным числом обусловленности).
При каких значениях  задача является плохо обусловленной? Ответ на этот вопрос зависит от конкретной вычислительной задачи. Обычно полагают плохо обусловленными задачами задачи с числом обусловленности, на много превышающим единицу.
задача является плохо обусловленной? Ответ на этот вопрос зависит от конкретной вычислительной задачи. Обычно полагают плохо обусловленными задачами задачи с числом обусловленности, на много превышающим единицу.
Пример хорошо и плохо обусловленных вычислительных задач классической корректной задачи 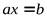
 ,
,  ,
, 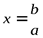 ,
,  ,
,  ,
,  ,
,  и
и 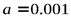 :
:


Т.е. при a = 1 имеем Dx*=1×Db, а при a = 0.001 имеем Dx*=103×Db.
Пример Дж. Уилкинсона
Рассмотрим задачу о вычислении корней многочлена 20-й степени  .
.
В качестве многочлена 20-й степени возьмем простой многочлен  .
.
Очевидно, что решение задачи 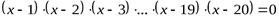 существует и единственно:x1 = 1, x2 = 2, …, x20 = 20. Доказано, что эта задача устойчива относительно возмущения исходных данных (коэффициентов). Т.е. задача корректна.
существует и единственно:x1 = 1, x2 = 2, …, x20 = 20. Доказано, что эта задача устойчива относительно возмущения исходных данных (коэффициентов). Т.е. задача корректна.
Предположим, что исходные данные — коэффициенты многочлена, содержат погрешности. Рассматриваемая задача плохо обусловлена, если малые погрешности исходные данных приводят к большим погрешностям решения (решение — корни многочлена).
Уилкинсон рассмотрел пример, когда коэффициент многочлена  при
при  ,
,  , содержит малую ошибку:
, содержит малую ошибку: 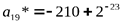 .
.
Вычислим корни возмущенного многочлена 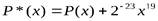 высокоточным алгоритмом и посмотрим, как столь незначительная погрешность влияет на значения корней?
высокоточным алгоритмом и посмотрим, как столь незначительная погрешность влияет на значения корней?
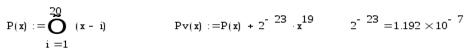


Т.е. если  — решение задачиP(x)=0, a
— решение задачиP(x)=0, a  — решение задачиP*(x)=0, погрешность исходных
— решение задачиP*(x)=0, погрешность исходных  и
и  , то
, то 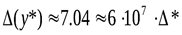 . Задача плохо обусловлена.
. Задача плохо обусловлена.
Видно, что первые шесть корней оказались практически нечувствительными к возмущению исходных данных, их погрешность не превышает  ; погрешности последующих корней растут, причем относительные погрешности некоторых корней приближаются к 20%.
; погрешности последующих корней растут, причем относительные погрешности некоторых корней приближаются к 20%.
Пример Дж.Уилкинсона — классический пример плохо обусловленной вычислительной задачи. Степень рассмотренного многочлена довольно велика. Однако плохо обусловленной может быть и задача о вычислении корней многочленов невысоких степеней. Рассмотрим задачу о вычислении корней многочлена 4-й степени  и соответствующую возмущенную задачу
и соответствующую возмущенную задачу 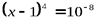 . (свободный член дан с относительной погрешностью
. (свободный член дан с относительной погрешностью  . Корни возмущенного многочлена
. Корни возмущенного многочлена  и
и 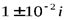 , их относительная погрешность
, их относительная погрешность  — задача плохо обусловлена.
— задача плохо обусловлена.
|
из
5.00
|
Обсуждение в статье: Обусловленность вычислительной задачи |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

