 |
Главная |
Идеальное с точки зрения сходимости .
|
из
5.00
|
МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
Рекомендовано
Методическим советом ДВГУПС
в качестве учебного пособия
Хабаровск
Издательство ДВГУПС
2012
УДК 517.962 (075.8)
ББК В 161.69я73
Р 844
Рецензенты:
Доктор физико-математических наук, заведующий отделом
теоретической и прикладной математики
Института прикладной математики ДВО РАН
А.В. Устинов
Кандидат физико-математических наук, доцент кафедры
«Информатика и информационные технологии» ДВГГУ
И.А. Ледовских
Рукавишников, А.В.
Р 844 Метод конечных разностей : учеб. пособие / А.В. Рукавишников, В.А. Рукавишников. – Хабаровск: Изд-во ДВГУПС, 2012. – 83 с.: ил.
Излагаются основные положения теории разностных схем и ее применения для различных классов задач.
Учебное пособие предназначено для студентов 4–5-го курсов очной формы обучения, изучающих дисциплины «Геометрическое моделирование в САПР» и «Модели и методы анализа проектных решений», а также для аспирантов и преподавателей инженерных специальностей.
УДК 517.962 (075.8)
ББК В 161.69я73
© ДВГУПС, 2012
ВВЕДЕНИЕ
Многие естественные процессы и явления описываются с помощью дифференциальных уравнений. Встает вопрос: как численно найти решение поставленной задачи, какой вычислительный метод при этом выбрать? В настоящем пособии в качестве численного подхода предлагается использовать метод конечных разностей, основанный на замене производных разностными отношениями. В результате такой замены получаем разностную схему решения исходной задачи, при численном решении которой, естественно возникают вопросы: о сходимости и скорости сходимости приближенного решения к точному решению дифференциальной задачи, от чего она зависит. В связи с этим познакомимся с понятиями аппроксимации и устойчивости разностной схемы, их взаимосвязью со сходимостью, а также убедимся в том, что наугад выбранная, аппроксимирующая исходную задачу на решении, разностная схема приводит к неутешительному результату, а именно, в большинстве случаев численно полученное решение не сходится к истинному решению дифференциальной задачи. Поэтому основное внимание необходимо заострить на способах проверки устойчивости при выборе разностной схемы.
При подготовке этого пособия ставилась цель: дать студентам в доступной форме необходимые сведения о методе конечных разностей как способе приближенного решения дифференциальных задач, представляющих практический интерес. Следует отметить, что все теоретические аспекты метода в разработке, для удобства, подробно разобраны на конкретных примерах. В ходе изучения предложенного в пособии материала можно проследить взаимосвязь представленной теории с уже изученными дисциплинами из математического цикла на более ранних курсах.
Пособие состоит из трех разделов.
Первый раздел посвящен построению разностных схем для обыкновенных дифференциальных уравнений, сначала даны интуитивные определения объектов рассмотрения, раскрывающие их сущность, а по мере погружения в материал – их точные математические формулировки.
Второй раздел – построению разностных схем для уравнений с частными производными. В частности, знакомит с особенностями построения численного метода решения уравнения Пуассона на плоскости, в области с криволинейной границей. Кроме этого, дается описание общего способа построения разностных схем, аппроксимирующих дифференциальное уравнение с заданной точностью, – метод неопределенных коэффициентов.
Третий раздел пособия знакомит читателя с методом повышения точности разностной схемы, на основе разностных схем меньшей точности, – экстраполяция Ричардсона.
1. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
1.1. Понятие о порядке точности и об аппроксимации
Этот подраздел посвящен вопросу сходимости решений разностных уравнений при измельчении сетки к решениям дифференциальных уравнений, которые они приближают.
1.1.1. Понятие о сетке и сеточной функции
Дифференциальную задачу будем записывать в виде символьного равенства:
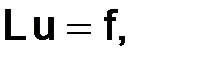 (1.1)
(1.1)
где 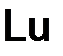 – левая, а
– левая, а 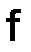 – правая части дифференциальной задачи.
– правая части дифференциальной задачи.
Пример. Запишем задачу
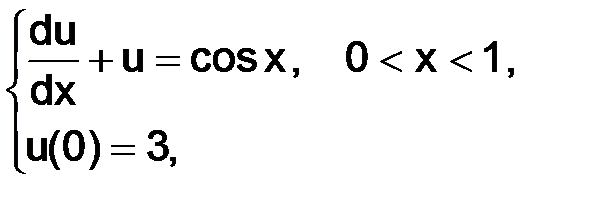 (1.2)
(1.2)
в виде (1.1)
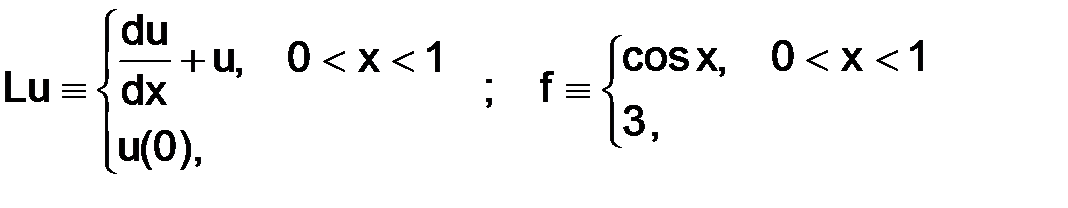 .
.
Отметим, что пока, для простоты, краевую дифференциальную задачу (1.1) будем рассматривать на отрезке 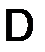 (то есть ограничимся одномерным случаем). Пусть
(то есть ограничимся одномерным случаем). Пусть  .
.
Определение. Сеткой назовем совокупность конечного числа точек на отрезке 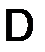 , которую будем обозначать через
, которую будем обозначать через 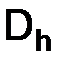 .
.
Определение. Через 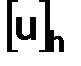 обозначим совокупность значений решения
обозначим совокупность значений решения 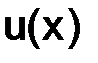 задачи (1.1) в точках сетки
задачи (1.1) в точках сетки 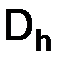 (узлах), которую назовем сеточной функцией.
(узлах), которую назовем сеточной функцией.
Предполагается, что сетка 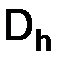 зависит от параметра
зависит от параметра 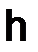 , который может принимать сколь угодно малые положительные значения.
, который может принимать сколь угодно малые положительные значения.
Разбиение отрезка D:
x0 x1 x2 x3 xN
.
0 1
Можно положить 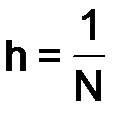 ,
,  – натуральное число и принять за сетку
– натуральное число и принять за сетку 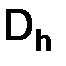 совокупность точек
совокупность точек 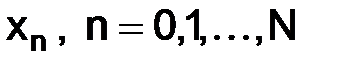 (индекс n – целое число):
(индекс n – целое число): 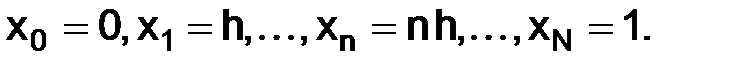
Определение. Параметр 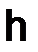 будем называть шагом сетки
будем называть шагом сетки 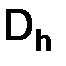 .
.
Искомая сеточная функция 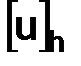 в точках
в точках 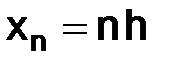 сетки
сетки 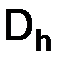 принимает значение
принимает значение 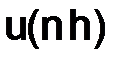 , т. е.
, т. е. 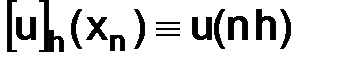 . Для приближенного нахождения функции
. Для приближенного нахождения функции 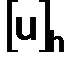 воспользуемся следующим методом.
воспользуемся следующим методом.
Рассмотрим задачу
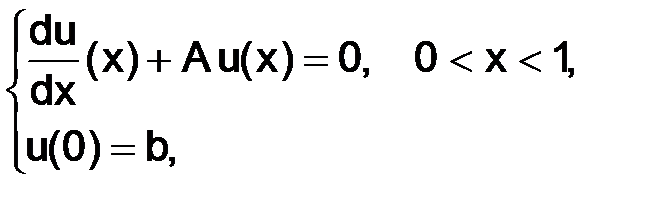
(1.3)
где А и b – заданные числа.
Заменяем производную 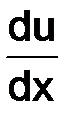 в (1.3) на разностное отношение
в (1.3) на разностное отношение 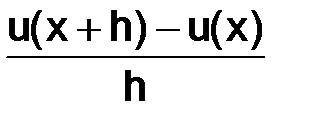 , тогда уравнение (1.3) примет вид:
, тогда уравнение (1.3) примет вид:
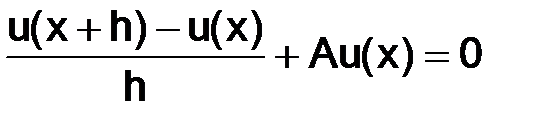 . (1.4)
. (1.4)
Обозначение. Приближенное значение, искомой функции 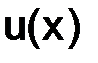 в узлах
в узлах 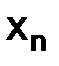 сетки
сетки 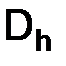 будем обозначать через
будем обозначать через 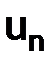 , а их совокупность – через
, а их совокупность – через 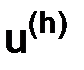 .
.
Перепишем (1.4) согласно введенным обозначениям в узлах сетки 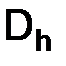 :
:
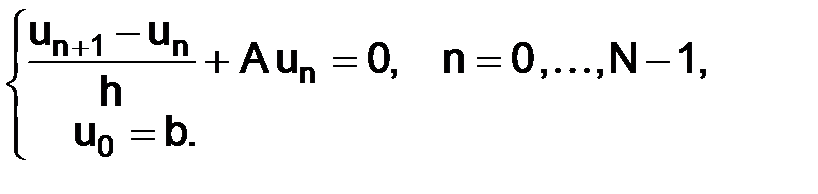 (1.5)
(1.5)
Определение. Систему вида (1.5) будем записывать следующим образом:
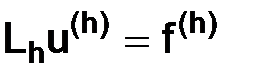 (1.6)
(1.6)
и называть разностной схемой для задачи (1.3)
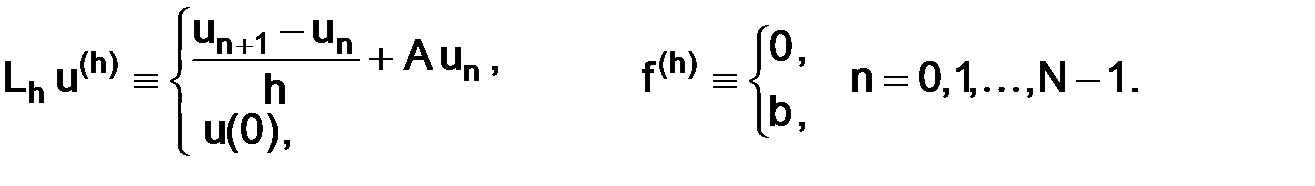
Замечание. Приближенное решение 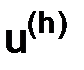 , т. е. то решение, которое мы находим с помощью разностной схемы (1.6), определено на той же самой сетке
, т. е. то решение, которое мы находим с помощью разностной схемы (1.6), определено на той же самой сетке 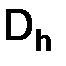 , что и сеточная функция
, что и сеточная функция 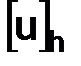 .
.
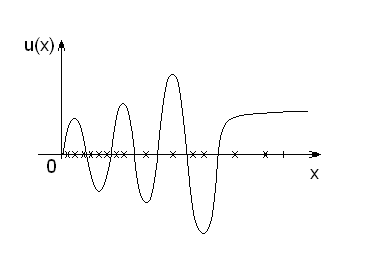 Рис. 1.1. Сетка с неравномерными шагами (со сгущением узлов вблизи нуля)
Рис. 1.1. Сетка с неравномерными шагами (со сгущением узлов вблизи нуля)
|
 может состоять из точек, которые расположены неравномерно на
может состоять из точек, которые расположены неравномерно на 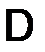 ; выбором расположения точек
; выбором расположения точек 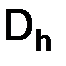 можно добиться того, чтобы искомая функция
можно добиться того, чтобы искомая функция 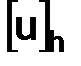 решения
решения 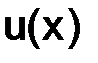 была подробнее при фиксированном N на тех участках, где
была подробнее при фиксированном N на тех участках, где 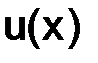 быстро меняется (рис. 1.1).
быстро меняется (рис. 1.1).
Пример.
Набор шагов: 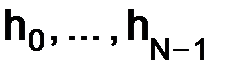 ,
,
набор узлов: 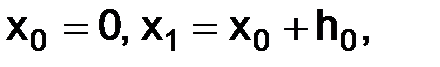
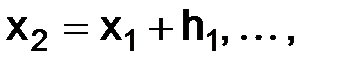
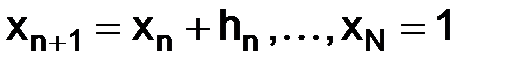 ;
; 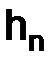 – выбирать произвольным, но таким, чтобы
– выбирать произвольным, но таким, чтобы 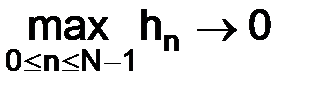 при
при 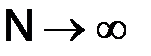 .
.
Отметим, что всюду в дальнейшем, если не оговорено противное, будем считать, что 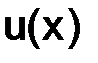 – непрерывная функция и обладает необходимым числом непрерывных производных на
– непрерывная функция и обладает необходимым числом непрерывных производных на  .
.
Цель. Наша задача состоит в отыскании 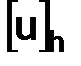 в точках
в точках 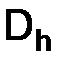 с помощью функции
с помощью функции 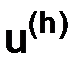 , которая «сходится» к
, которая «сходится» к 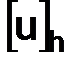 при измельчении сетки
при измельчении сетки 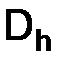 . Для этой цели будем использовать разностные уравнения.
. Для этой цели будем использовать разностные уравнения.
1.1.2 Порядок точности разностной схемы
Вернемся к приближенному решению задачи (1.3). Выразим значение 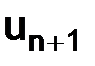 через
через 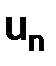 в (1.5):
в (1.5):
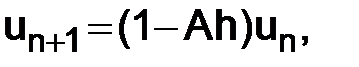

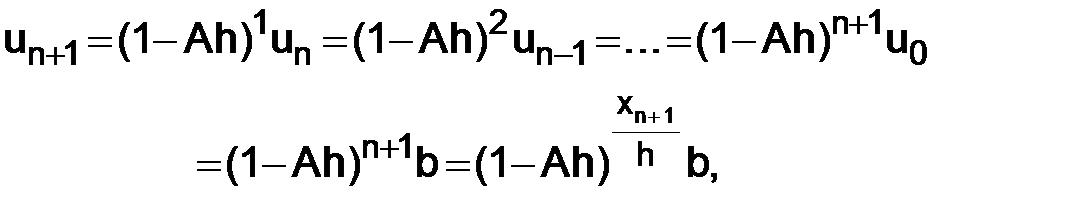
т. е.
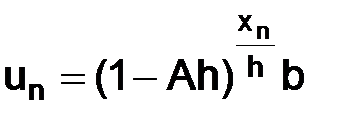 . (1.7)
. (1.7)
Известно, что решение дифференциального уравнения первого порядка (1.3) имеет вид (проверить, подставив его в уравнение)
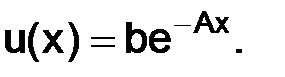 (1.8)
(1.8)
Найдем оценку величины погрешности приближенного решения (1.5) в узлах сетки 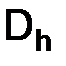 :
:
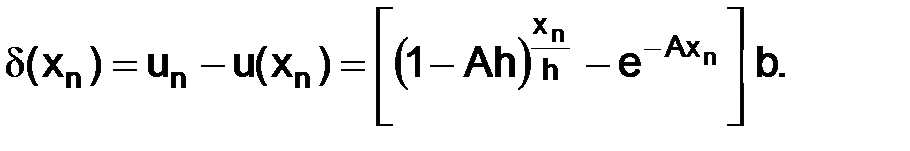 (1.9)
(1.9)
Нас будет интересовать, как убывает величина погрешности 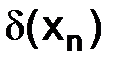 при увеличении числа точек N разбиения отрезка [0,1], или, что то же самое при уменьшении шага
при увеличении числа точек N разбиения отрезка [0,1], или, что то же самое при уменьшении шага 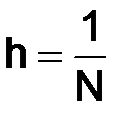 сетки
сетки 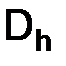 .
.
Определение. Будем говорить, что функция 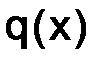 ограничена относительно функции
ограничена относительно функции 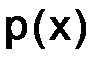 на некотором промежутке S (
на некотором промежутке S ( 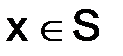 ) и записывать равенством
) и записывать равенством 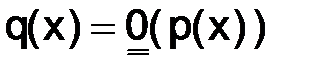 , если существует такая положительная константа C, что для любого значения
, если существует такая положительная константа C, что для любого значения 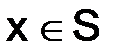 выполняется неравенство
выполняется неравенство 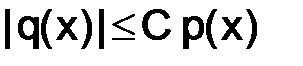 .
.
Из курса математического анализа известна формула Тейлора
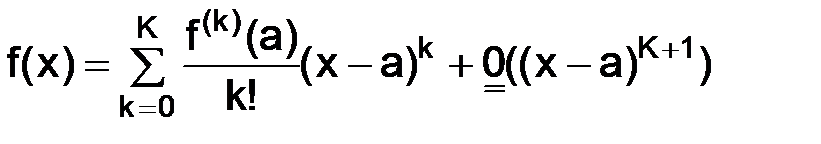 ,
,
разложение функции  в окрестности точки
в окрестности точки  с остаточным членом в форме Пеано.
с остаточным членом в форме Пеано.
Раскладывая по степеням  в окрестности точки ноль, имеем
в окрестности точки ноль, имеем
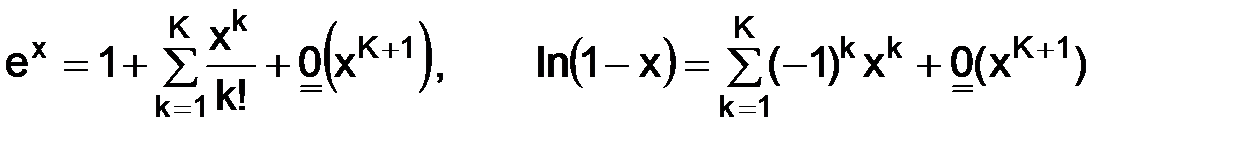 .
.
Следовательно, над выражением 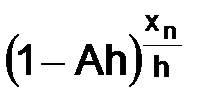 можно провести цепочку преобразований:
можно провести цепочку преобразований:
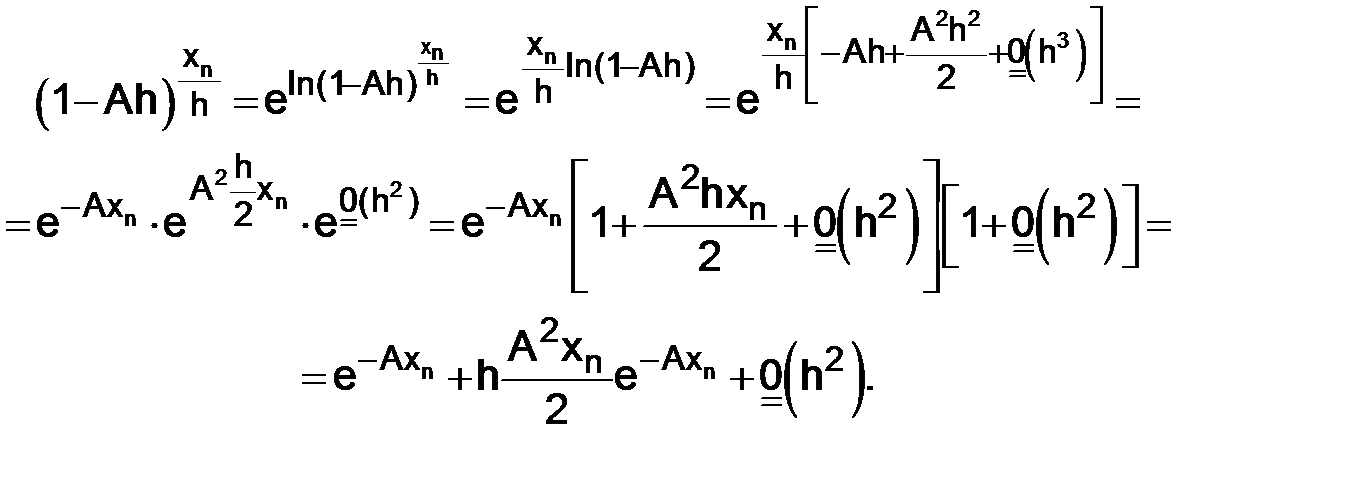
Таким образом, равенство (1.7) примет вид:
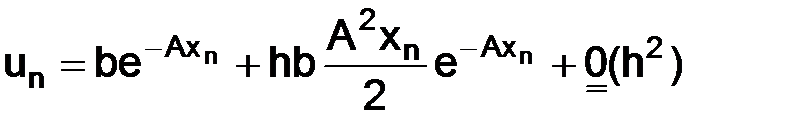 (1.10)
(1.10)
и
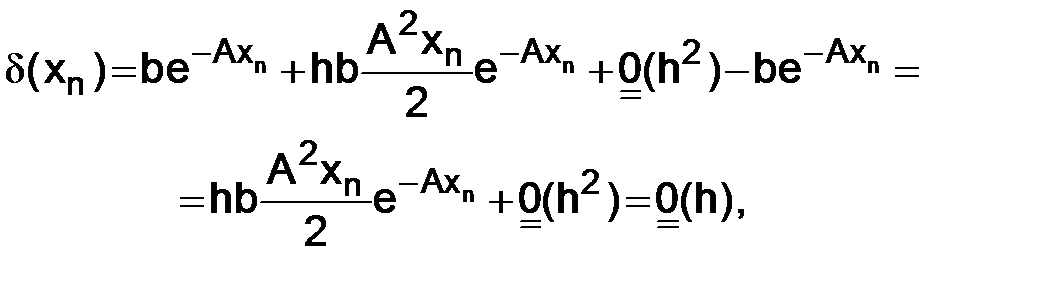 (1.11)
(1.11)
т. е. величина погрешности 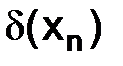 в (1.9) стремится к нулю при h→0 и имеет порядок первой степени по шагу сетки
в (1.9) стремится к нулю при h→0 и имеет порядок первой степени по шагу сетки 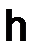 .
.
Вывод. В таком случае говорят, что разностная схема (1.5) имеет
первый порядок точности.
Заменим производную 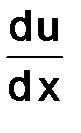 в (1.3) с помощью другого разностного отношения
в (1.3) с помощью другого разностного отношения 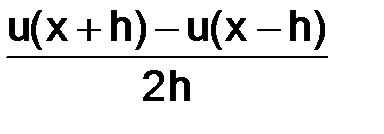 , тогда уравнение в (1.3) примет вид
, тогда уравнение в (1.3) примет вид
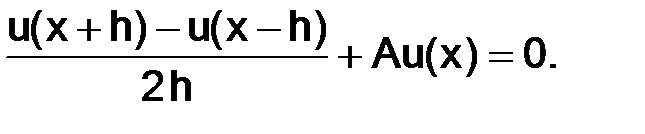 (1.12)
(1.12)
Перепишем уравнение (1.12) в узлах 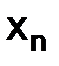 сетки
сетки 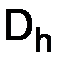 в следующем виде
в следующем виде
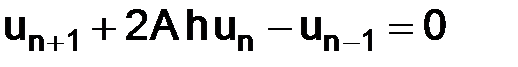 .
.
Замечание. Уравнение (1.12) является разностным уравнением второго порядка. Поэтому при построении на основе таких уравнений разностной схемы требуется задавать два начальных условия: u0 = u(0) и u1 = u(h), тогда как дифференциальное уравнение в (1.3) есть уравнение первого порядка и для него мы задаем только одно начальное условие: u(0) = b. В разностной схеме естественно положить u0 = b, но пока не ясно, как задавать значение u1.
Решение уравнения 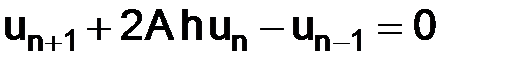 будем искать в следу-ющем виде:
будем искать в следу-ющем виде: 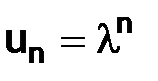 , следовательно, уравнение примет вид:
, следовательно, уравнение примет вид:
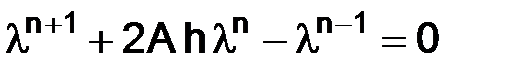 ,
,
а после сокращения на величину 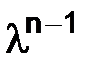 :
:
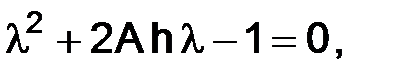
тогда его корни: 
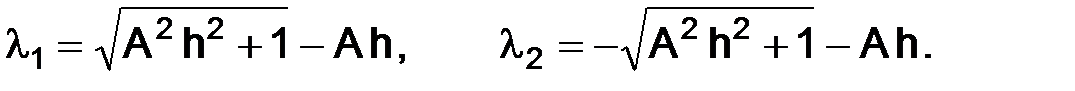
Заметим, что 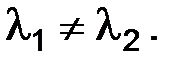 Следовательно, решение будет иметь общий вид:
Следовательно, решение будет иметь общий вид: 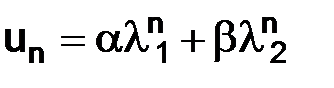 , где
, где 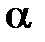 и
и 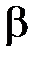 некоторые числа, найдем их:
некоторые числа, найдем их:
1) пусть n = 0, тогда 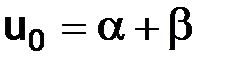 ;
;
2) пусть n = 1, тогда 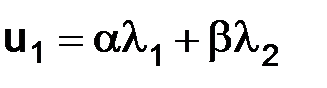 ;
;
3) разрешая систему уравнений 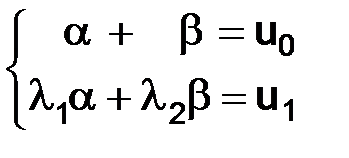 относительно
относительно 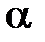 и
и 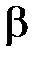 , получаем
, получаем 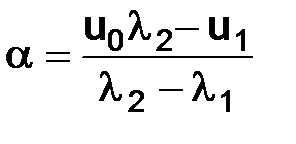 и
и 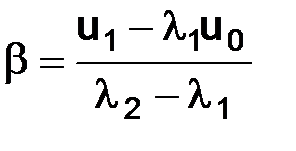 , т. е.
, т. е.
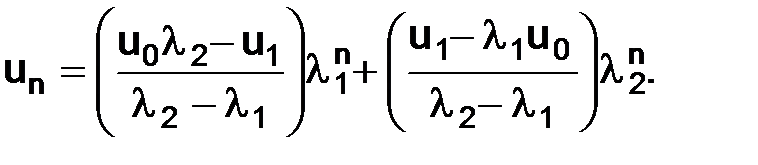 (1.13)
(1.13)
Разложим функцию 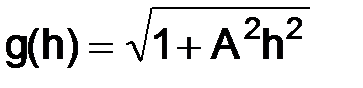 по формуле Тейлора в окрестности точки ноль, тогда будем иметь
по формуле Тейлора в окрестности точки ноль, тогда будем иметь
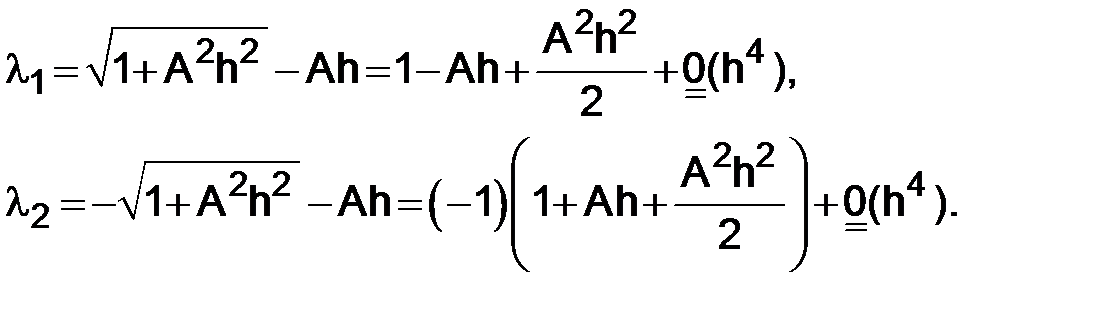 (1.14)
(1.14)
Разложения (1.14) дают приближенные представления для 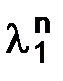 и
и 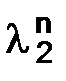 :
:
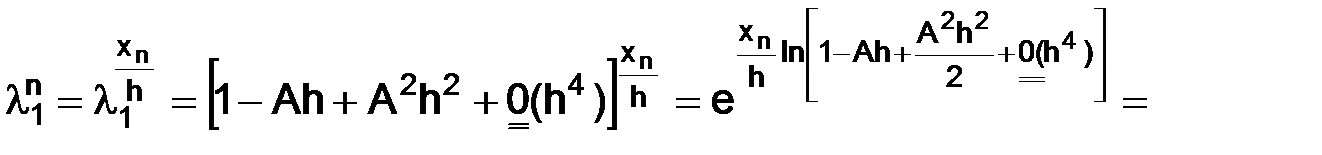
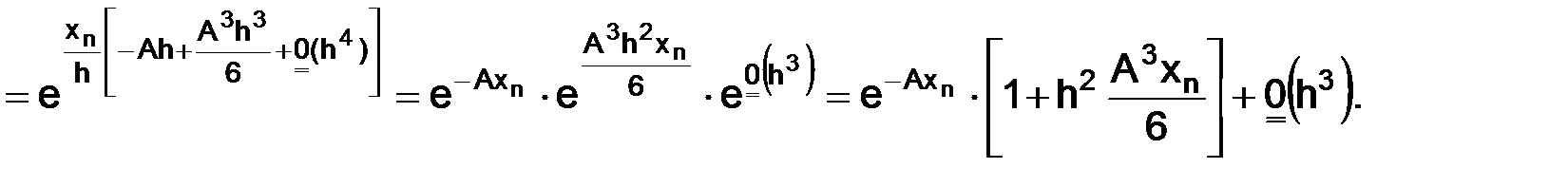
Пояснение. Сначала воспользовались разложением функции 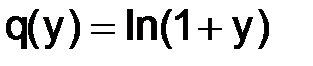 по формуле Тейлора в окрестности точки ноль (y = 0):
по формуле Тейлора в окрестности точки ноль (y = 0): 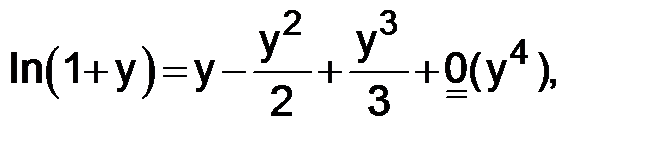 а затем подставили при условии, что
а затем подставили при условии, что 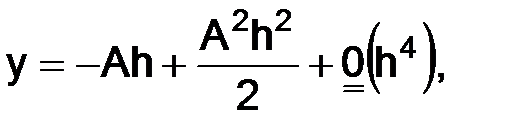 тогда
тогда
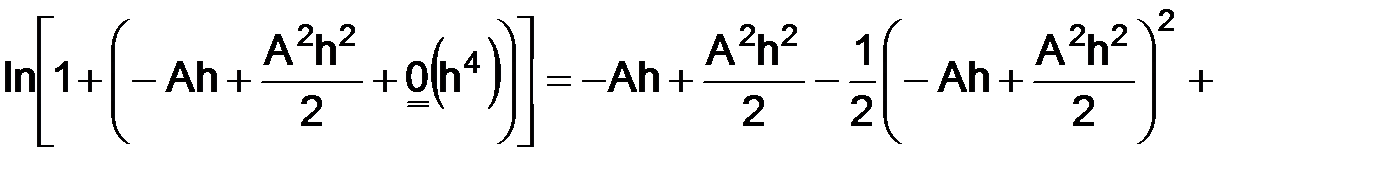
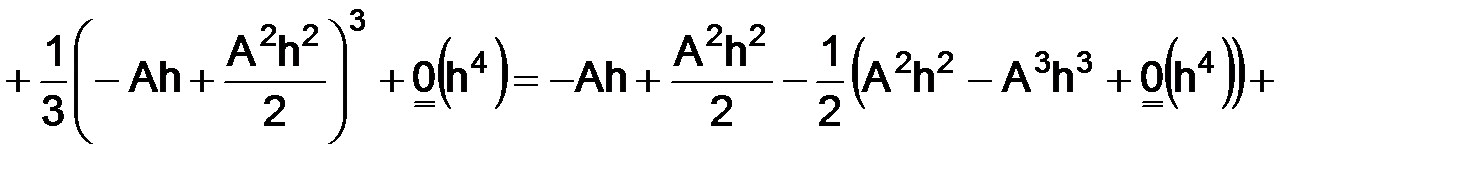
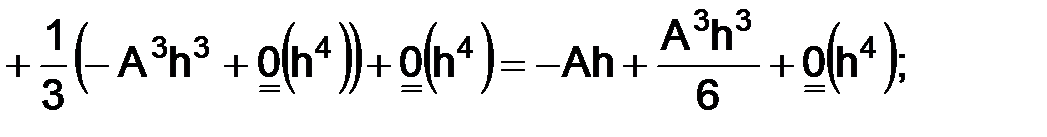
т. е.
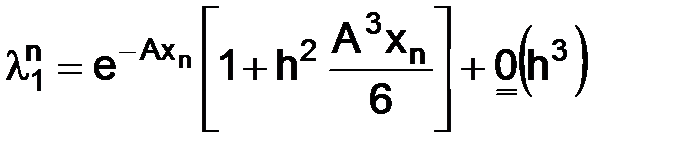 . (1.15)
. (1.15)
Убедитесь самостоятельно, что
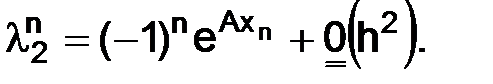 (1.16)
(1.16)
Подставим приближенные выражения для 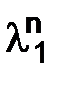 из (1.15) и
из (1.15) и 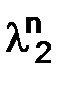 из (1.16) в (1.13), имеем
из (1.16) в (1.13), имеем
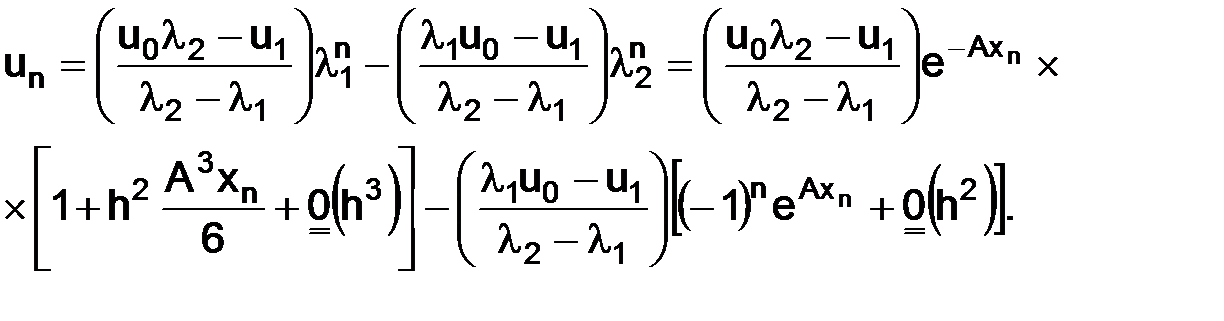 (1.17)
(1.17)
Замечание. Все дальнейшие выводы мы будем получать путем исследования формулы (1.17).
Отметим, что если коэффициент 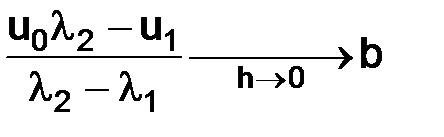 , то первое слагаемое (1.17) стремится к искомому решению (1.8) задачи (1.3).
, то первое слагаемое (1.17) стремится к искомому решению (1.8) задачи (1.3).
Так как
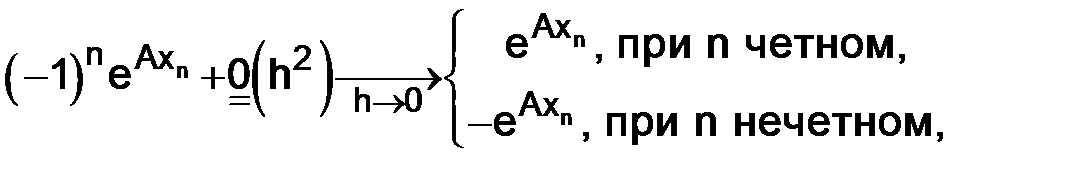
т. е. не сходится к определенному пределу для всех натуральных n, то для сходимости к пределу при h→0 второго слагаемого (1.17) нужно потребовать, чтобы

Подведем итог всему сказанному. Для того чтобы решение разностного уравнения 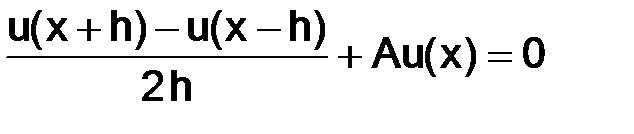 сходилось к решению
сходилось к решению  краевой задачи (1.3), необходимо выполнение условий
краевой задачи (1.3), необходимо выполнение условий
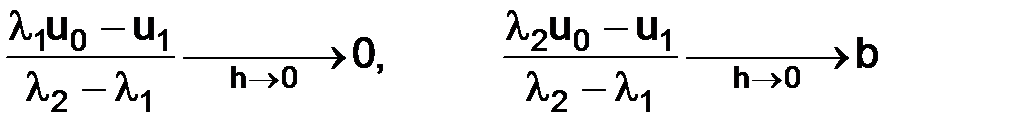 . (1.18)
. (1.18)
Напомним, что первое начальное условие – 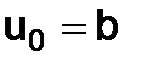 . Формулы (1.18) подсказывают, как можно задавать второе начальное условие
. Формулы (1.18) подсказывают, как можно задавать второе начальное условие 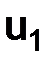 : так как
: так как 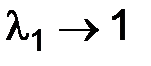 , а
, а 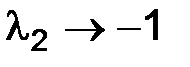 , при h→0, то условия (1.18) выполняются, если
, при h→0, то условия (1.18) выполняются, если 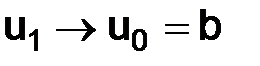 .
.
Теперь перейдем к изучению вопроса влияния способа задания начального условия 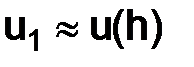 для решения задачи (1.3) с помощью системы разностных уравнений вида (1.12) в узлах сетки
для решения задачи (1.3) с помощью системы разностных уравнений вида (1.12) в узлах сетки 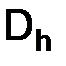 .
.
Для определения значения 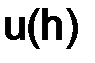 воспользуемся, во-первых, разложением функции
воспользуемся, во-первых, разложением функции 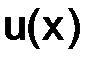 по формуле Тейлора в окрестности точки ноль (x = 0) и, во-вторых, самим дифференциальным уравнением:
по формуле Тейлора в окрестности точки ноль (x = 0) и, во-вторых, самим дифференциальным уравнением: 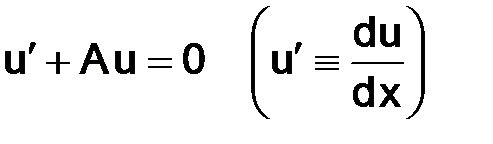 , тогда
, тогда
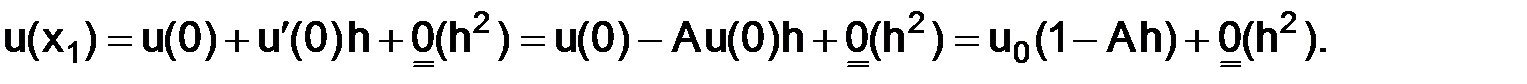
Значение  можно задавать следующими способами:
можно задавать следующими способами:
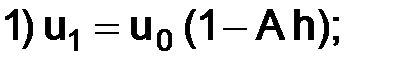
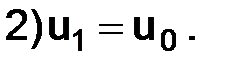
В первом случае мы допускаем в начальном значении 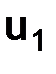 ошибку
ошибку
порядка 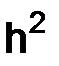 , а во втором – порядка h.
, а во втором – порядка h.
Выясним влияние точности задания начального условия 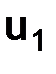 , на величину погрешности в решении, в каждом из случаев:
, на величину погрешности в решении, в каждом из случаев:
1) 
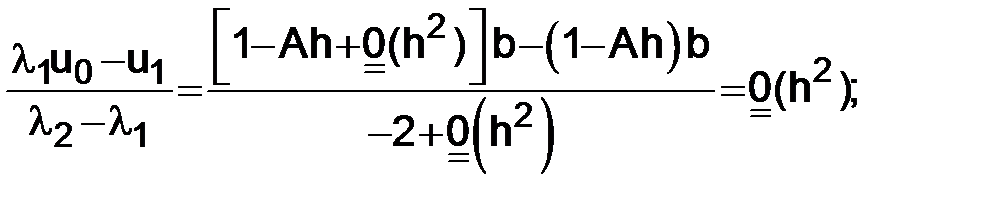
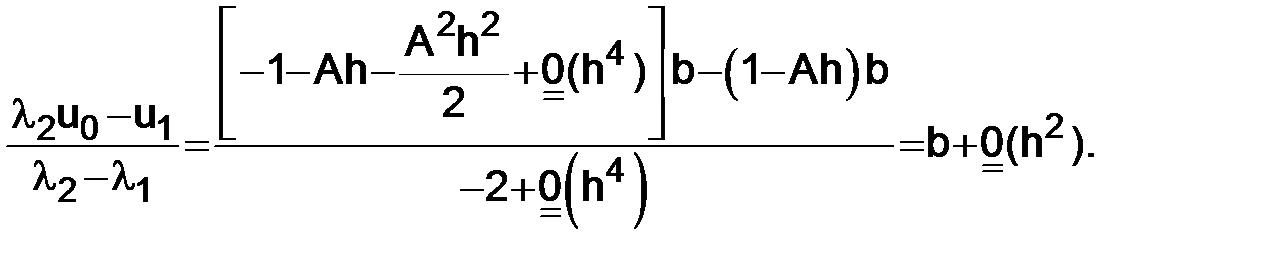
Отметим, что полученные разложения удовлетворяют (1.18) при  и, кроме того, подставляя в (1.17), получаем
и, кроме того, подставляя в (1.17), получаем
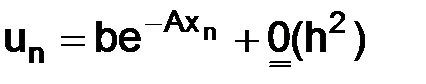 . (1.19)
. (1.19)
2) 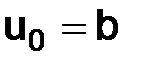 ,
, 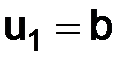 :
:
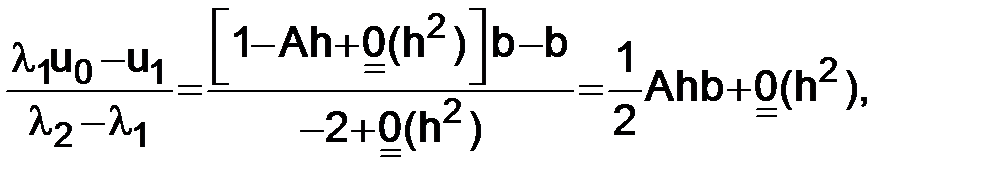
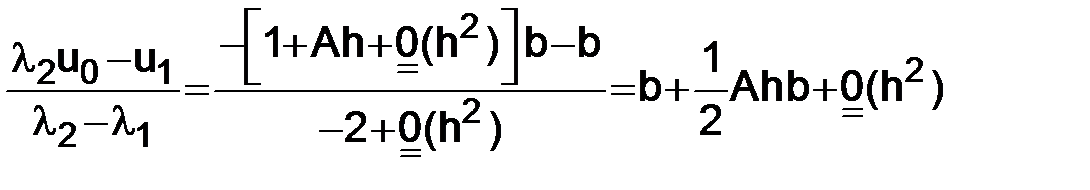
и, следовательно, подставляя в (1.17)
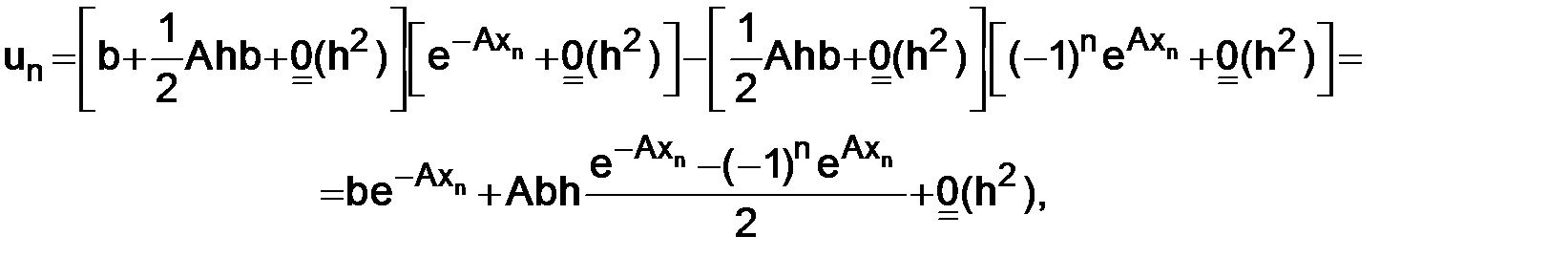
т. е.
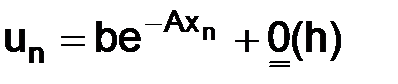 . (1.20)
. (1.20)
Таким образом, если допустить в начальных данных ошибку порядка h, то и ошибка в решении (1.20) будет порядка h.
Следовательно, если начальное значение u1 задается с точностью до величины порядка h2, то и величина погрешности решения будет порядка h2,
т. е. разностная схема имеет второй порядок точности.
Вывод. Решение с помощью разностных уравнений
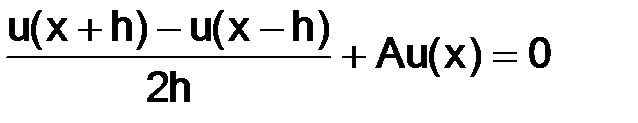 (1.21)
(1.21)
в отличие от
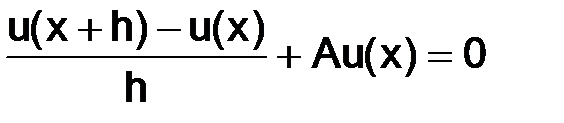 (1.22)
(1.22)
может дать более высокий порядок точности, а именно, точность с остаточным членом порядка h2, а не порядка h, как (1.22). Чтобы получить второй порядок точности, надо, задавая точное 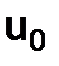 , выбирать
, выбирать 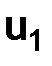 , отличающееся от значения точного решения дифференциального уравнения в точке
, отличающееся от значения точного решения дифференциального уравнения в точке 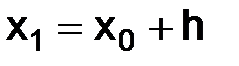 , на величину порядка h2. Если задавать начальное значение
, на величину порядка h2. Если задавать начальное значение 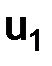 с ошибкой порядка h, то и решение получим с ошибкой того же порядка.
с ошибкой порядка h, то и решение получим с ошибкой того же порядка.
1.1.3. Порядок аппроксимации разностной схемы
Интересно понять, с чем связано то обстоятельство, что решение с помощью разностного уравнения
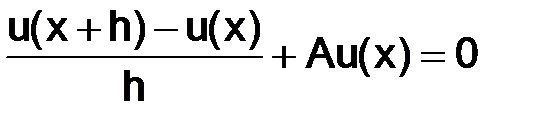
оказывается менее точным, чем с помощью
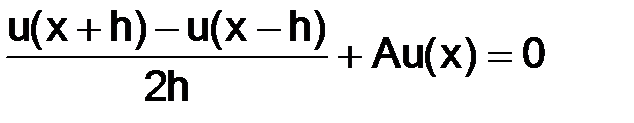 .
.
Эти разностные уравнения различаются приближенными выражениями для производной 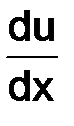 в точке x.
в точке x.
Заменим 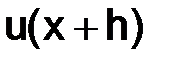 и
и 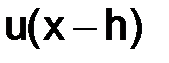 их тейлоровскими разложениями в окрестности точки
их тейлоровскими разложениями в окрестности точки  :
:
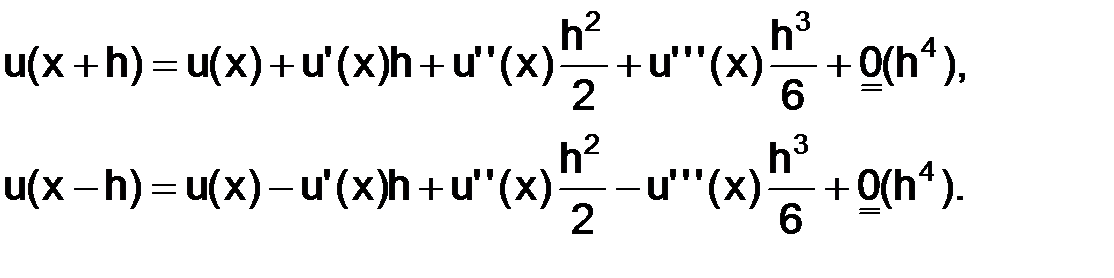
Пользуясь ими, получим
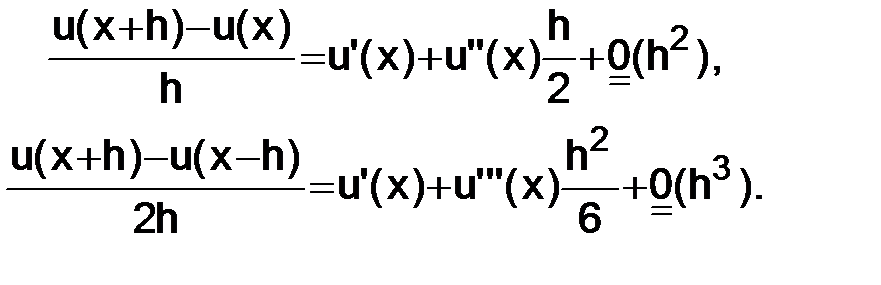
В первом случае мы имеем аппроксимацию (т. е. разность между производной и разностным отношением) с первым порядком точности, а во втором – со вторым порядком.
Замечание. Рассмотренные примеры наводят на мысль: порядок точности решения разностных уравнений (порядок сходимости приближенного решения, полученного с помощью разностных уравнений, к точному решению в узлах сетки 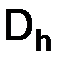 ) может быть сделан равным порядку аппроксимации производных дифференциального уравнения. Однако оказывается, что в такой общей формулировке эта гипотеза неверна. На разностные схемы, для которых будет доказана ее справедливость нам придется наложить одно весьма существенное ограничение – требование устойчивости. Необходимость этого ограничения станет ясной из следующего примера.
) может быть сделан равным порядку аппроксимации производных дифференциального уравнения. Однако оказывается, что в такой общей формулировке эта гипотеза неверна. На разностные схемы, для которых будет доказана ее справедливость нам придется наложить одно весьма существенное ограничение – требование устойчивости. Необходимость этого ограничения станет ясной из следующего примера.
1.1.4. Неустойчивая разностная схема
Вернемся к рассмотрению задачи (1.3). Для составления разностной схемы приближающей это уравнение, достаточно заменить производную 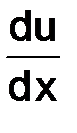 каким-либо аппроксимирующим ее разностным отношением. Мы рассмотрели в предыдущих подпунктах разностные отношения
каким-либо аппроксимирующим ее разностным отношением. Мы рассмотрели в предыдущих подпунктах разностные отношения 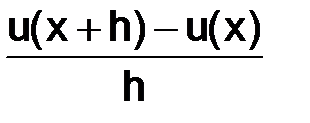 и
и 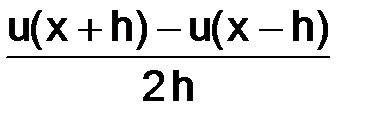 , очевидно также, что любое выражение вида
, очевидно также, что любое выражение вида
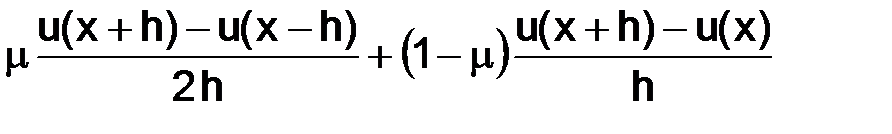
будет приближать 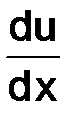 в точке
в точке  , где
, где 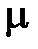 – произвольное число. В самом деле
– произвольное число. В самом деле

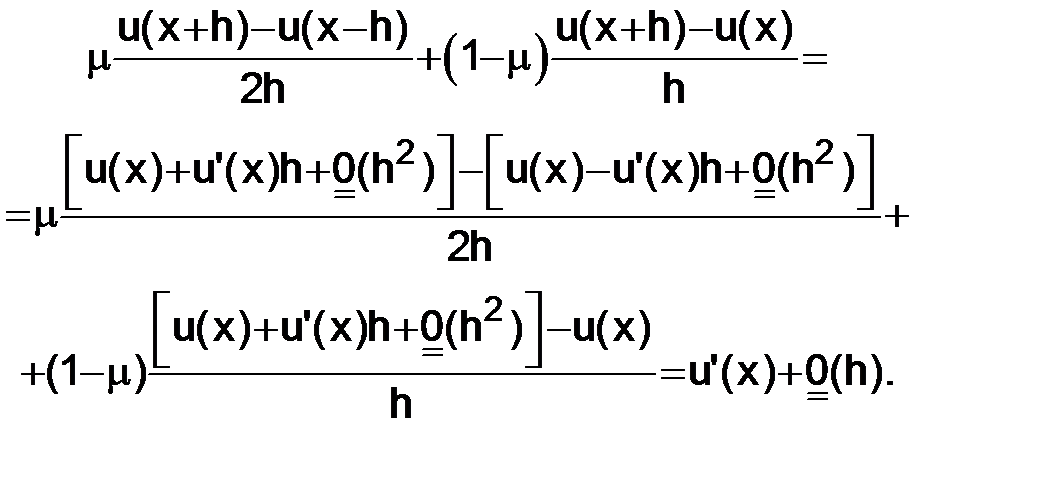
Получаем семейство разностных уравнений, определяющих семейство разностных схем при фиксированном шаге сетки 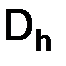 :
:
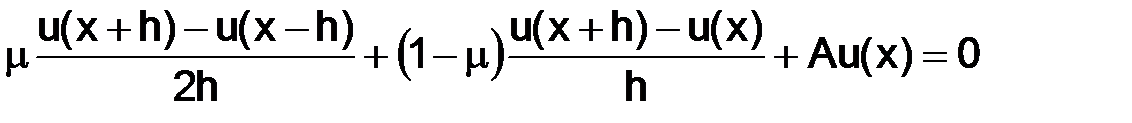 ,
,
каждому значению µ отвечает своя схема. Ранее мы рассматривали случаи 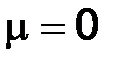 и
и 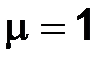 .
.
Рассмотрим разностное уравнение, определяющее разностную схему с шагом 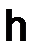 при
при 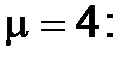
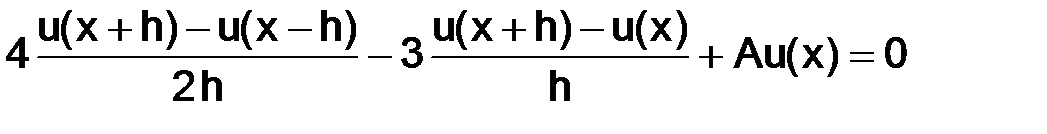 .
.
Перепишем уравнение в следующем виде:
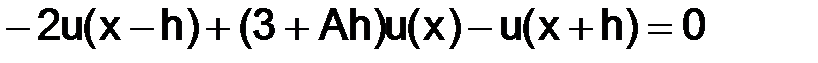 ,
,
тогда решение, полученное с помощью соответствующей разностной схемы, запишем в виде (1.13), предварительно сделав необходимые элементарные преобразования:
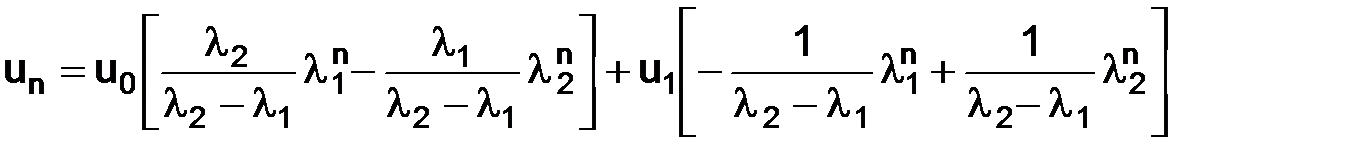 ,
,
где 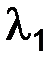 и
и 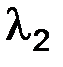 – корни квадратного уравнения
– корни квадратного уравнения
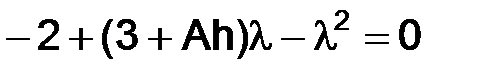 .
.
С помощью разложений по формуле Тейлора в окрестности точки ноль, с остаточным членом в форме Пеано, представим корни 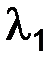 и
и 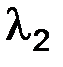 , а затем
, а затем 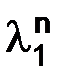 и
и 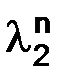 :
:
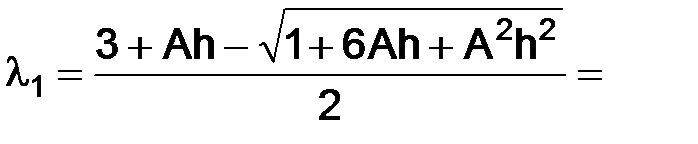
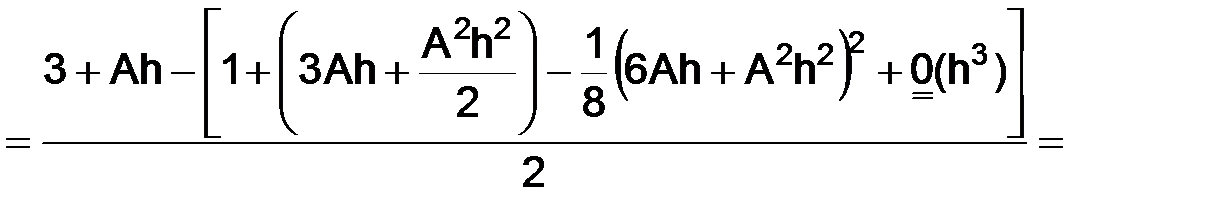
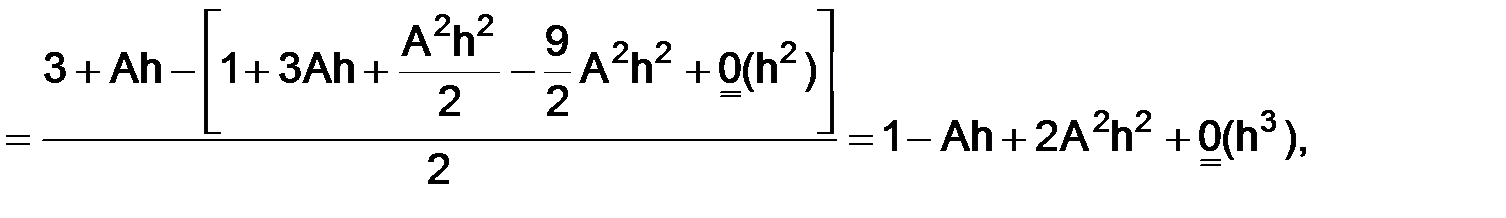
т. е. 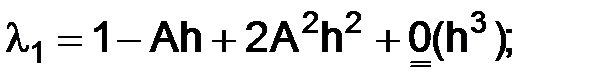
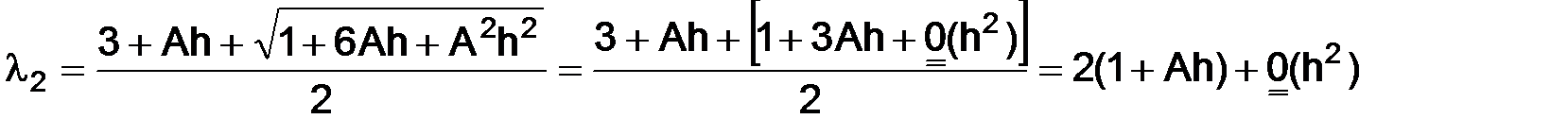 ,
,
т. е. 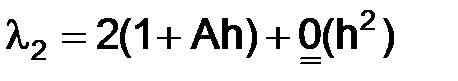 , тогда
, тогда 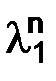 и
и 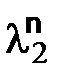 :
:
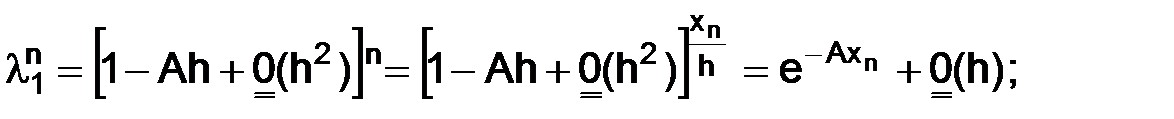
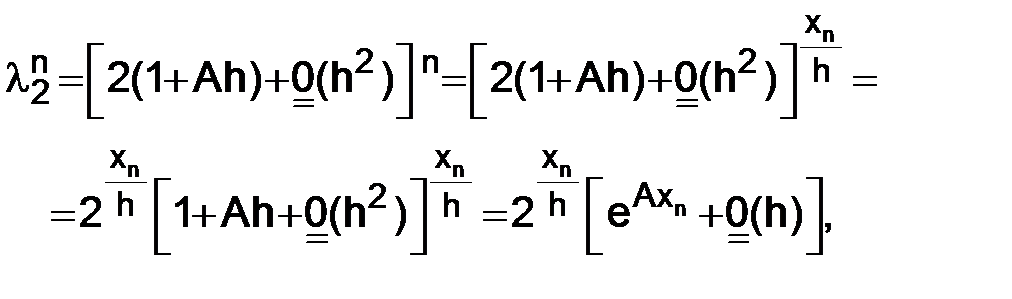
т. е. 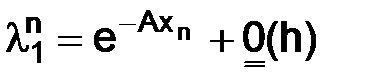 и
и 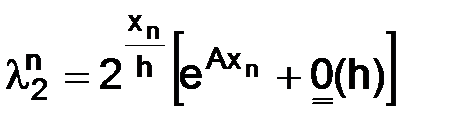 ,
,
следовательно,
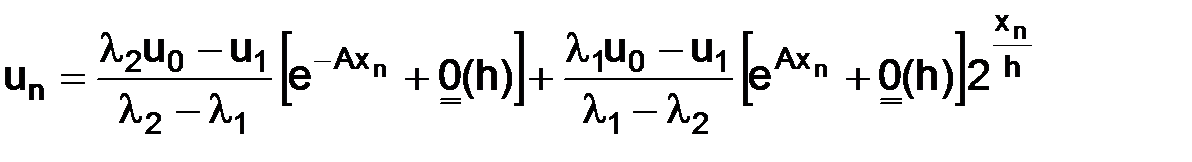 . (1.23)
. (1.23)
Прежде чем исследовать, к чему стремится 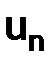 при
при 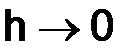 , мы должны указать, как задаются начальные условия
, мы должны указать, как задаются начальные условия 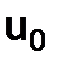 и
и 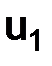 разностного решения. Рассматриваем задачу (1.3), тогда
разностного решения. Рассматриваем задачу (1.3), тогда 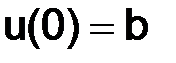 , следовательно, возьмем в качестве начальных данных
, следовательно, возьмем в качестве начальных данных 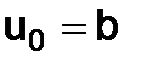 и
и 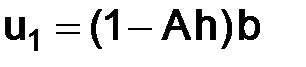 и подставим в формулу (1.23)
и подставим в формулу (1.23)
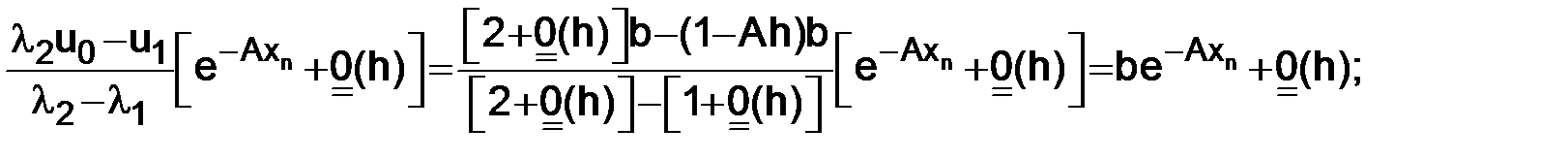
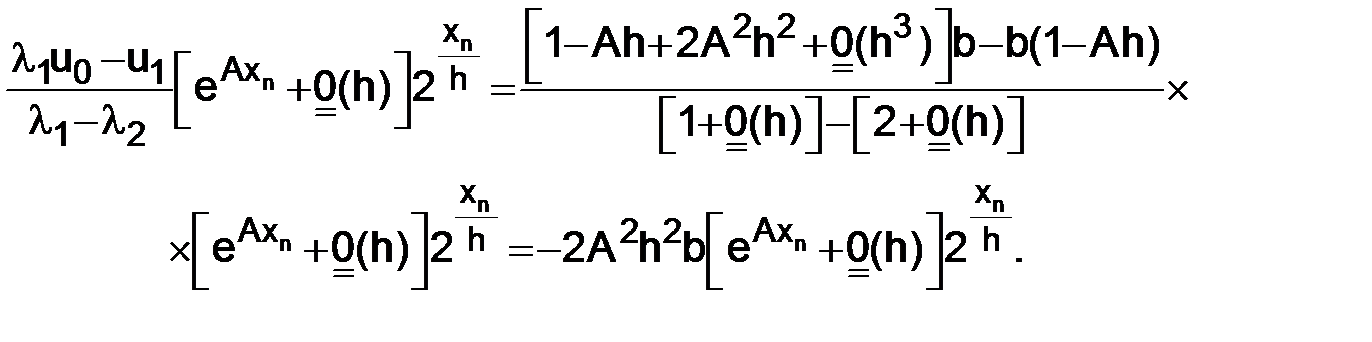
Таким образом, получим
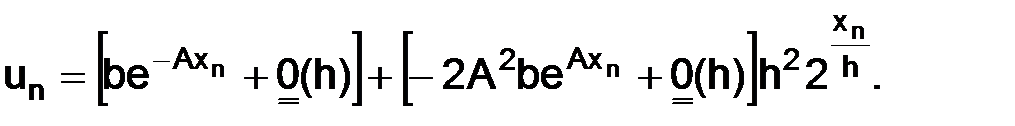
Первое слагаемое при h→0 стремится к решению (1.8), чтобы к нему сходилось все выражение для un, необходимо, чтобы второе слагаемое стремилось к нулю при h→0.
Однако это не так: 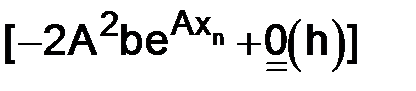 стремится к конечному и не равному нулю пределу
стремится к конечному и не равному нулю пределу 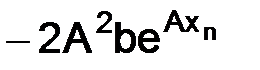 , а
, а 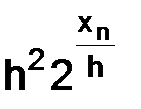 стремится к бесконечности быстрее любой положительной степени
стремится к бесконечности быстрее любой положительной степени 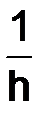 .
.
Вывод. Мы показали, что разностная схема, аппроксимирующая дифференциальное уравнение, может иметь решение, не сходящееся при h→0 к решению дифференциального уравнения.
Можно подумать, что причина этого в недостаточно точном выборе значения u1. Однако мы сейчас покажем, что сходимости не будет, даже если выбрать u1 точно равным решению дифференциального уравнения в точке 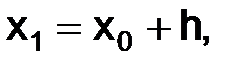 т. е. положить
т. е. положить 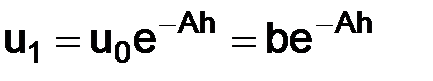 .
.
Вычислим
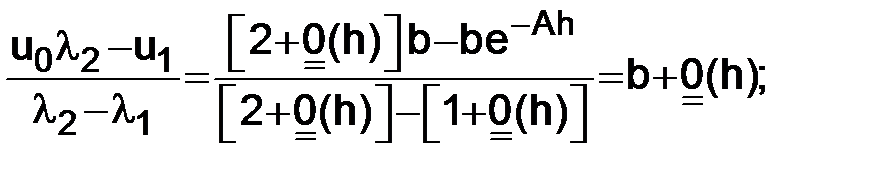
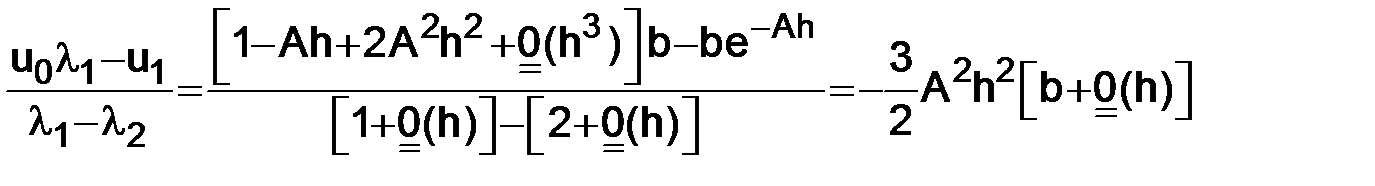 ,
,
тогда
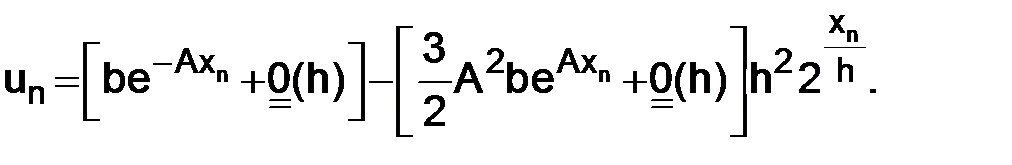
Второй член снова стремится к бесконечности при h→0.
Замечание. Такого рода разностные схемы называются неустойчивыми. Естественно, что они не пригодны для численного решения дифференциального уравнения.
1.2. Сходимость разностной схемы
В предыдущем подразделе, на примерах выяснили, что такое аппроксимация дифференциальной задачи разностной задачей и в чем состоит сходимость, благодаря которой решение дифференциальной задачи можно приближенно вычислить с помощью разностной схемы. Мы познакомились с явлением неустойчивости, которое может сделать разностную схему расходящейся и не пригодной для вычислений.
В этом подразделе мы дадим строгое определение понятия сходимости. Покажем, что доказательство сходимости не обязательно основывается на анализе формул для решений.
1.2.1. Сходящиеся разностные схемы
Цель: придать точный смысл самому требованию сходимости 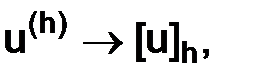 при
при 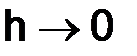 , который предъявляем к разностным схемам.
, который предъявляем к разностным схемам.
Определение. Линейное пространство  называется нормированным, если каждому элементу
называется нормированным, если каждому элементу  этого пространства
этого пространства  поставлено в соответствие неотрицательное число ||x|| – называемое нормой, при этом выполнены следующие три аксиомы:
поставлено в соответствие неотрицательное число ||x|| – называемое нормой, при этом выполнены следующие три аксиомы:
1) 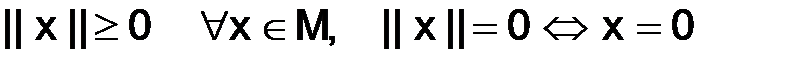 ;
;
2) 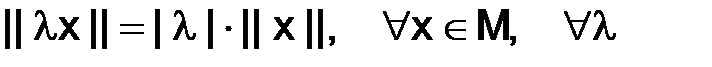 – число;
– число;
3) 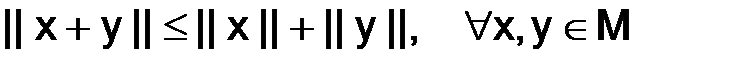 .
.
Обозначения. Если 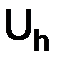 – нормированное пространство, то
– нормированное пространство, то 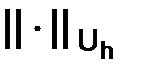 – значок нормы пространства
– значок нормы пространства 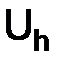 .
.
Примеры норм:
1. 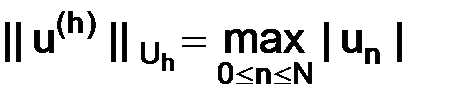 ; 2.
; 2. 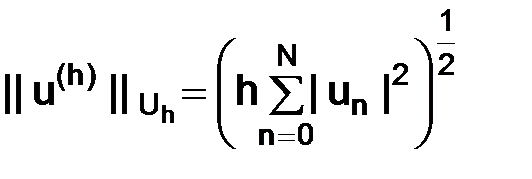 .
.
У приведенных выше норм дискретных пространств Uh есть соответствующие им аналоги норм непрерывных пространств U на отрезке 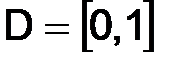 :
:
1. 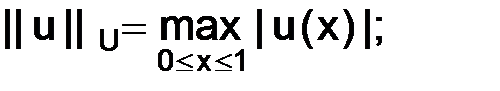 2.
2. 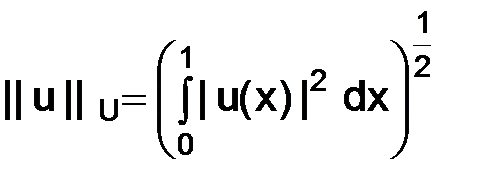 .
.
Убедитесь, что величина 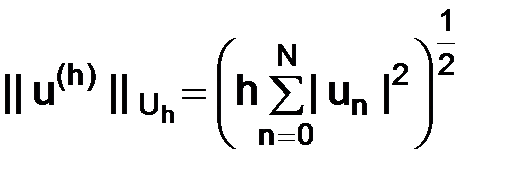 действительно является нормой (необходимо проверить справедливость всех трех аксиом).
действительно является нормой (необходимо проверить справедливость всех трех аксиом).
Всюду, где не оговорено противное, будем пользоваться первой нормой.
После того, как введено нормированное пространство 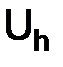 , приобретает смысл понятие отклонения одной функции от другой. Если
, приобретает смысл понятие отклонения одной функции от другой. Если 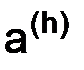 и
и 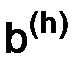 – две функции из пространства
– две функции из пространства 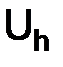 , то мерой их отклонения друг от друга считается норма их разности, т. е. число:
, то мерой их отклонения друг от друга считается норма их разности, т. е. число:
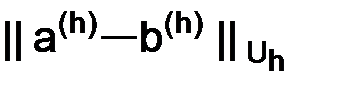 .
.
Теперь перейдем к строгому определению сходящейся разностной схемы. Пусть для приближенного вычисления решения дифференциальной краевой задачи (1.1) составлена система разностных уравнений (разностная схема), которую записываем, как и ранее
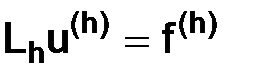 . (1.24)
. (1.24)
Отметим, что (1.24) (разностная краевая задача) – это не одна система, а семейство систем, зависящее от параметра 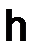 .
.
Будем полагать, что при каждом рассматриваемом достаточно малом шаге 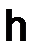 существует решение
существует решение 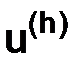 задачи (1.24), принадлежащее пространству
задачи (1.24), принадлежащее пространству 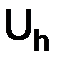 .
.
Определение. Будем говорить, что решение 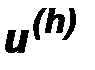 разностной краевой задачи (1.2.1) при измельчении сетки сходится к решению
разностной краевой задачи (1.2.1) при измельчении сетки сходится к решению 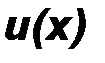 дифференциальной краевой задачи (1.1.1), если
дифференциальной краевой задачи (1.1.1), если
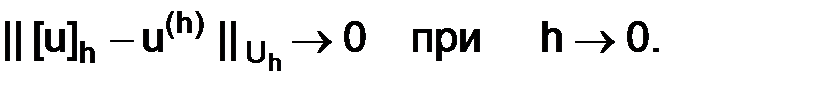 (1.25)
(1.25)
Если, сверх того, выполнено неравенство
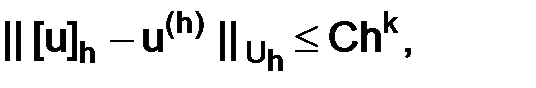 (1.26)
(1.26)
где


