 |
Главная |
Что и требовалось доказать.
|
из
5.00
|
Теперь покажем, что функция 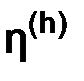 , определенная в узлах сетки
, определенная в узлах сетки 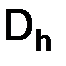 соотношением
соотношением
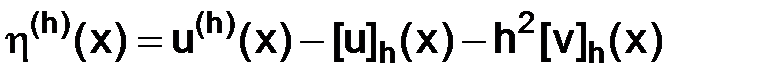 , (3.16)
, (3.16)
равномерно ограничена по  .
.
Здесь под равномерной ограниченностью подразумевается следующее: 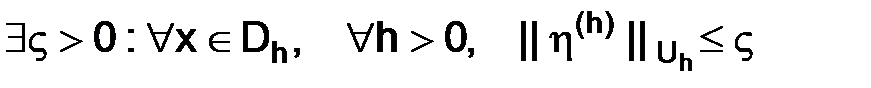 .
.
Рассмотрим выражение:
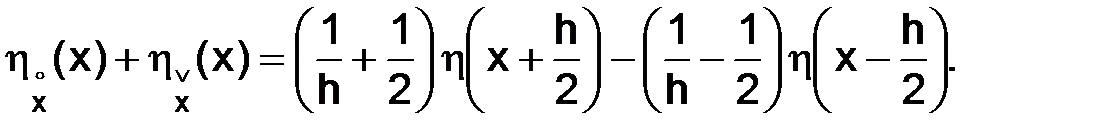
С учетом (3.1), получаем
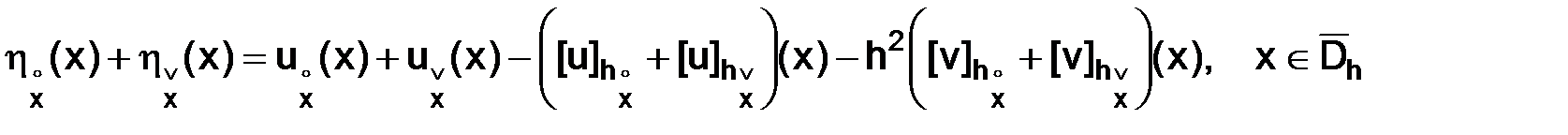 .
.
Зафиксируем некоторую точку 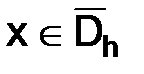 , и преобразуем правую часть последнего равенства. Сумма первых двух слагаемых равна
, и преобразуем правую часть последнего равенства. Сумма первых двух слагаемых равна 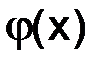 .
.
Далее, отметим, что
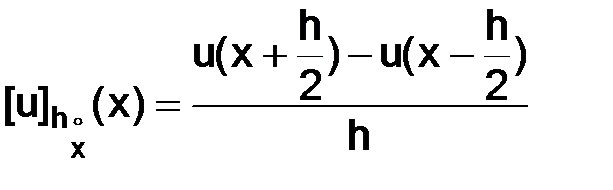 ,
, 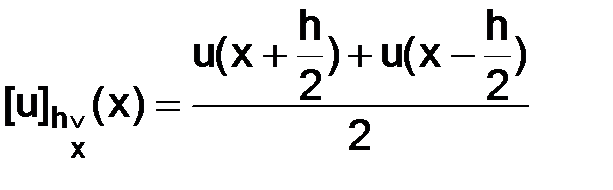 ,
,
тогда, используя разложения по формуле Тейлора в окрестности точки  с остаточным членом в форме Лагранжа, имеем следующие представления:
с остаточным членом в форме Лагранжа, имеем следующие представления:
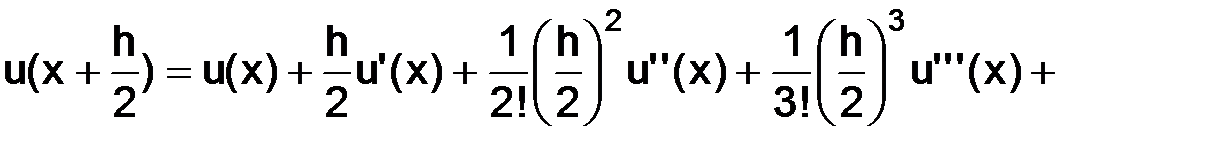
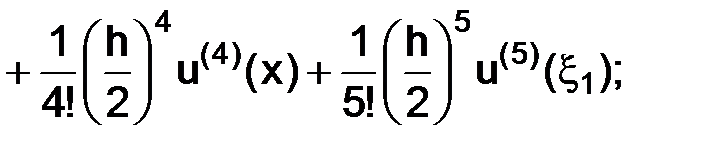
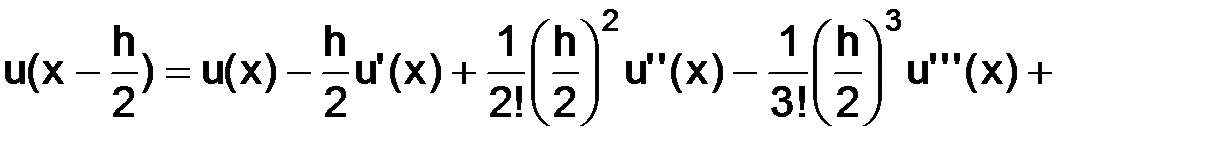
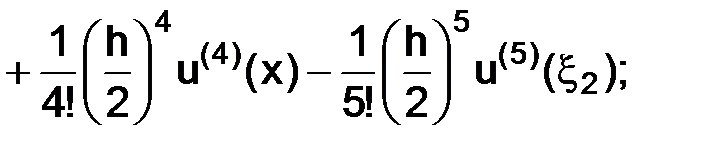
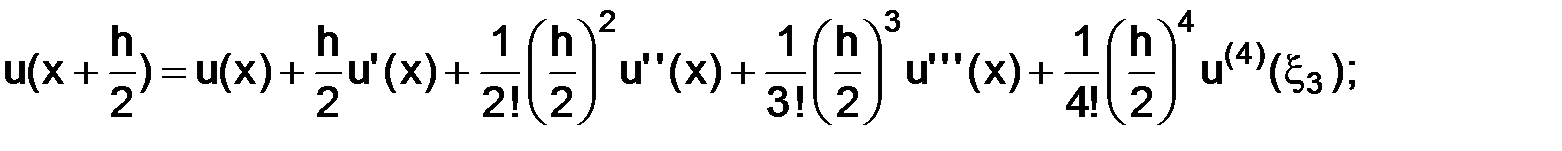
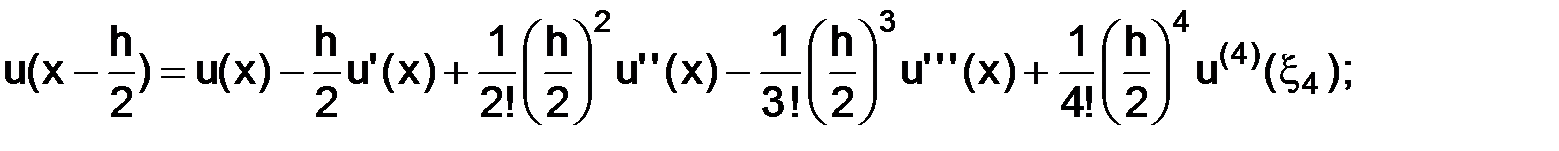
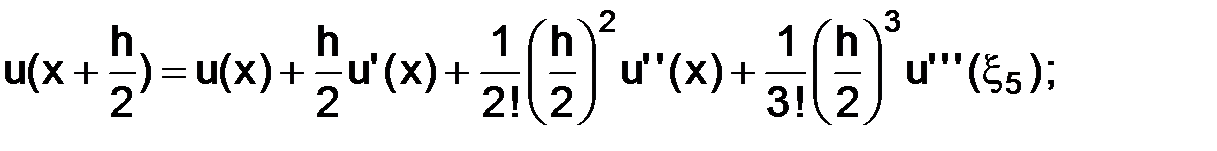
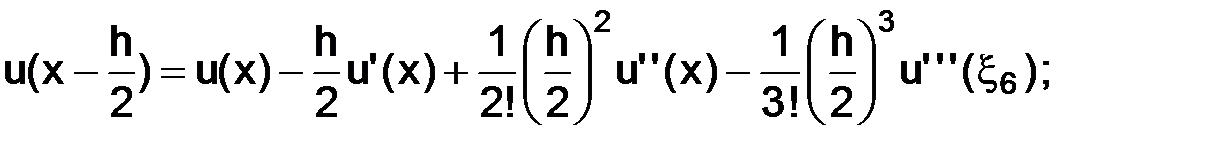
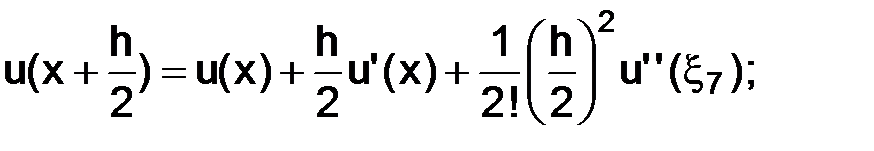
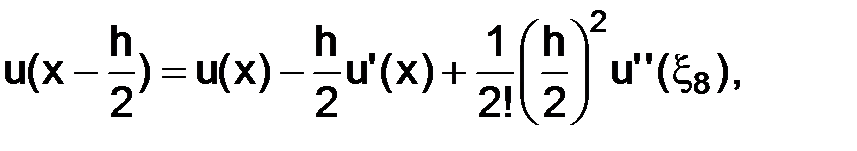
где точки 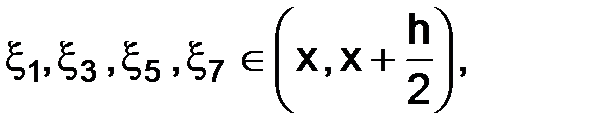 а
а 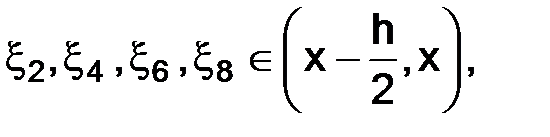 тогда
тогда
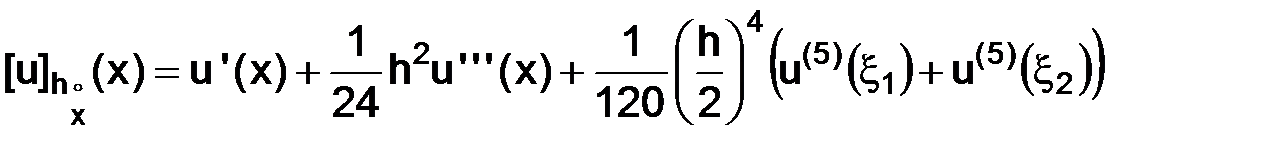 , (3.17)
, (3.17)
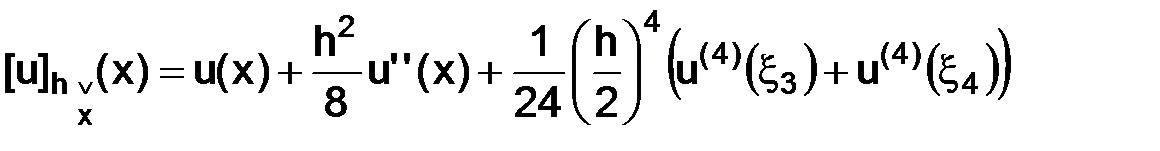 , (3.18)
, (3.18)
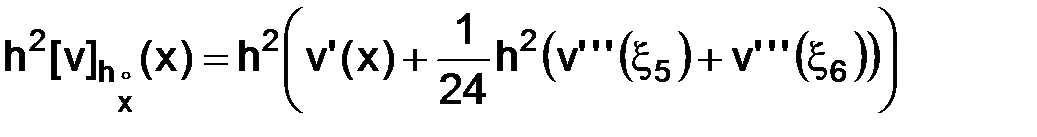 , (3.19)
, (3.19)
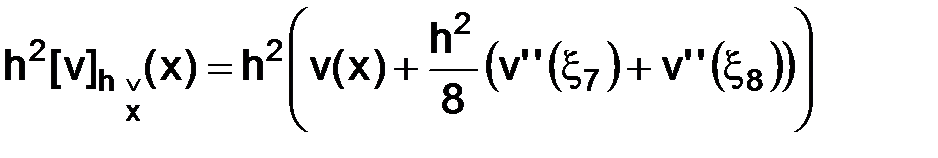 . (3.20)
. (3.20)
В результате применения (3.17), (3.18), (3.19), (3.20) получим
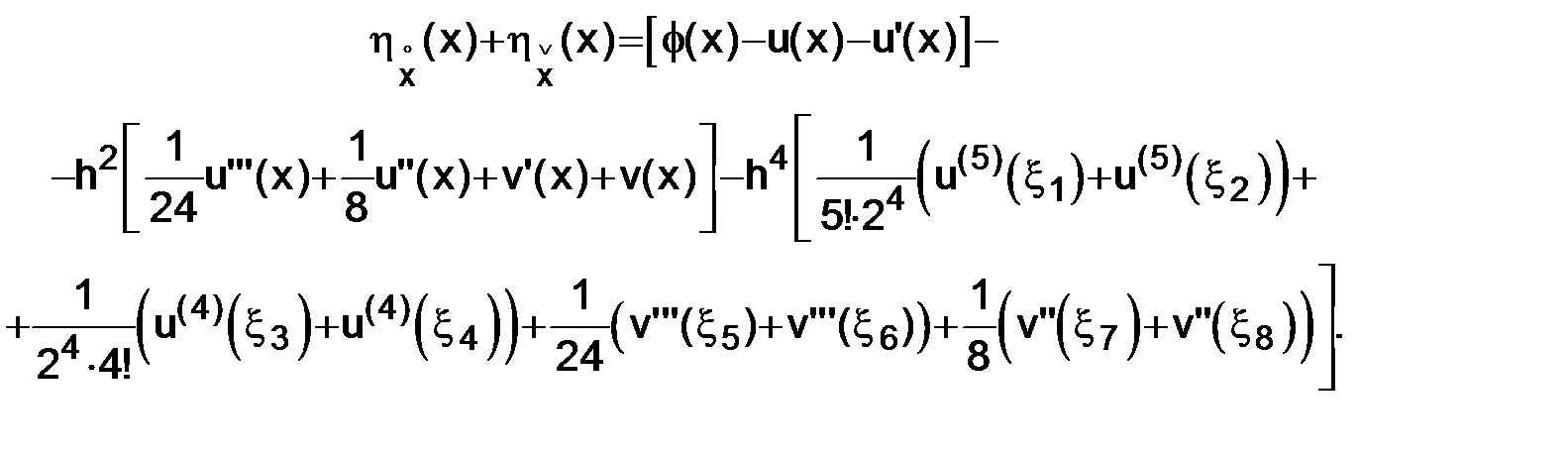 (3.21)
(3.21)
Поскольку любая производная от 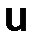 (x) и
(x) и  (x) непрерывна на
(x) непрерывна на 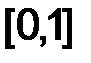 (а значит, ограничена), то правая часть (3.21) представляет собой величину, модуль которой ограничен числом
(а значит, ограничена), то правая часть (3.21) представляет собой величину, модуль которой ограничен числом 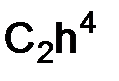 , где константа
, где константа 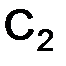 не зависит от
не зависит от 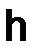 и
и  , при этом,
, при этом, 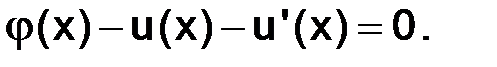 Учитывая сказанное, получим соотношение
Учитывая сказанное, получим соотношение
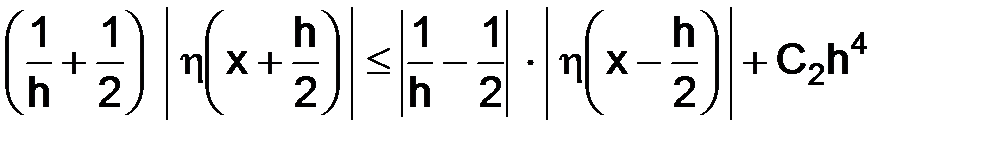 ,
,
из которого следует неравенство
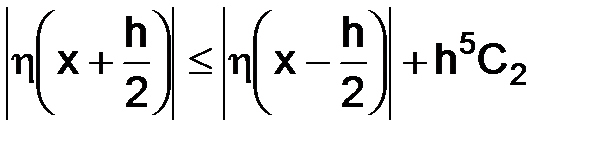 , (3.22)
, (3.22)
так как 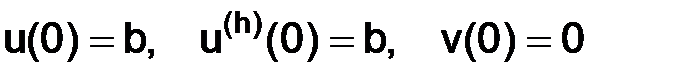 , следовательно, исходя из (3.1.16)
, следовательно, исходя из (3.1.16)
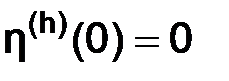 .
.
Поэтому из неравенства (3.22) выводится оценка
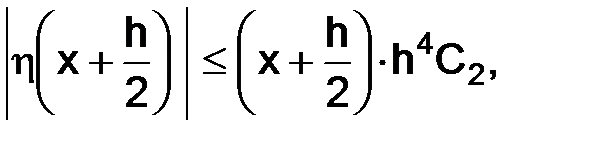
для любого 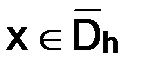 , так как
, так как 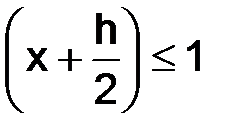 , то
, то
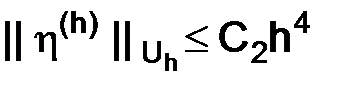 . (3.23)
. (3.23)
Тем самым мы показали, что при 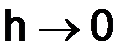 выполняется равенство
выполняется равенство
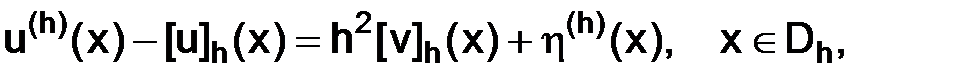
где
1) 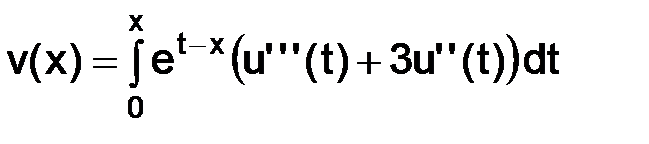 – гладкая функция, определенная на отрезке
– гладкая функция, определенная на отрезке 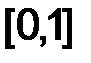 и не зависящая от
и не зависящая от 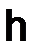 ;
;
2) 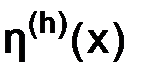 – функция, определенная в узлах сетки
– функция, определенная в узлах сетки 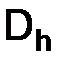 , со значениями порядка
, со значениями порядка 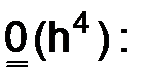
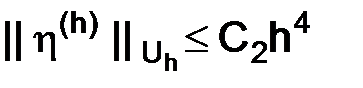 .
.
Изложим теперь метод повышения точности основанной на доказанном разложении. С этой целью построим сетки:
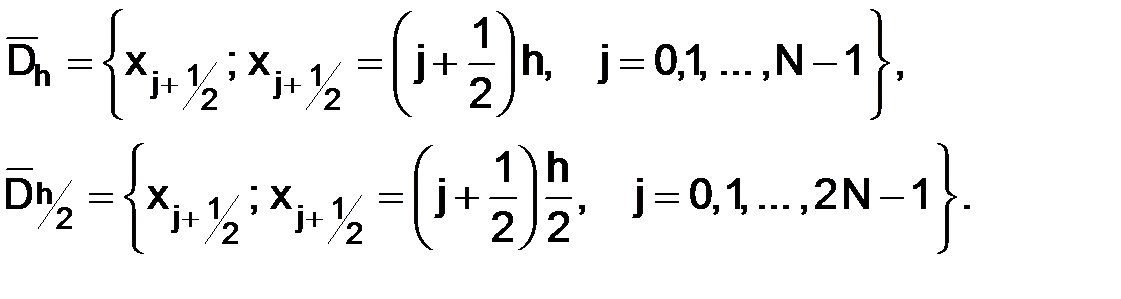
На каждой из них построим соответствующую разностную схему:
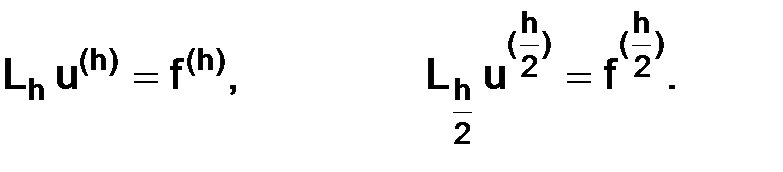 (3.24)
(3.24)
Пусть функции 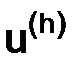 и
и 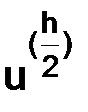 – решения, полученные с помощью разностных схем (3.24) (точность каждого из решений является величина порядка
– решения, полученные с помощью разностных схем (3.24) (точность каждого из решений является величина порядка 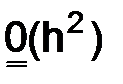 ). Составим в узлах сетки
). Составим в узлах сетки 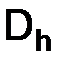 линейную комбинацию приближенных решений:
линейную комбинацию приближенных решений:
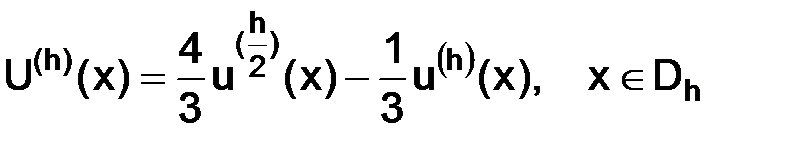 (3.25)
(3.25)
и покажем, что функция 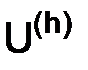 (x) приближает
(x) приближает 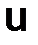 (x) с точностью четвертого порядка по шагу
(x) с точностью четвертого порядка по шагу 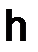 в узлах сетки
в узлах сетки 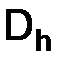 .
.
Согласно (3.6) справедливы разложения:
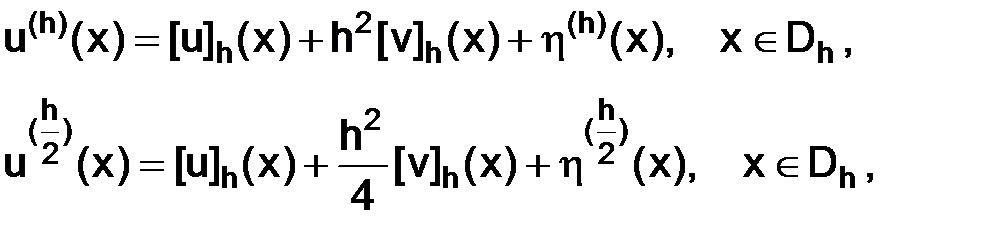
откуда, используя (3.25), следует, что
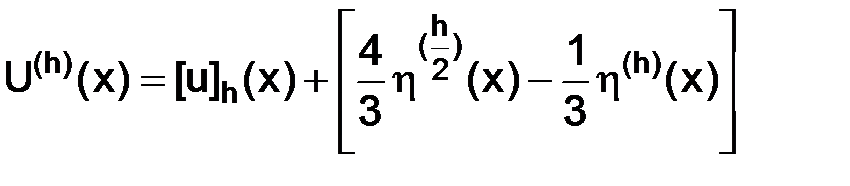 .
.
Учитывая оценку (3.23), будем иметь
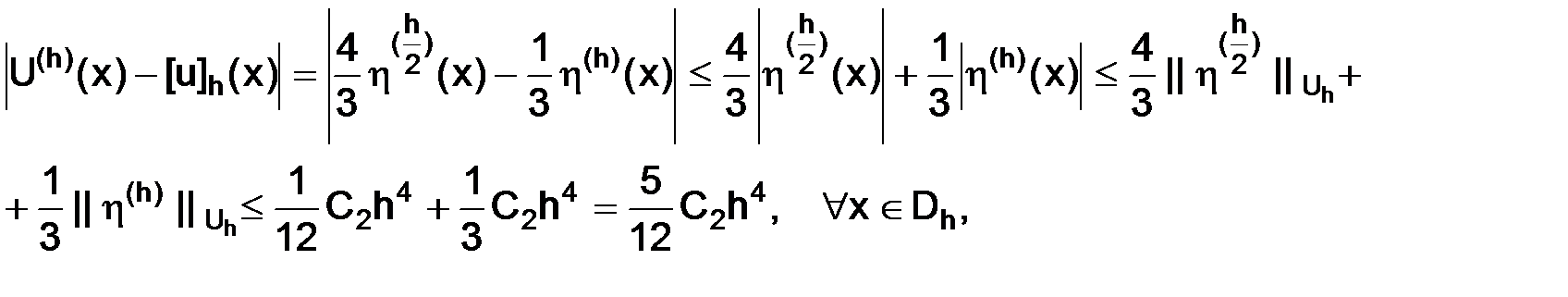
т. е. 
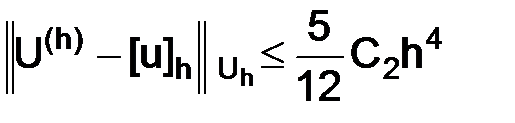 . (3.26)
. (3.26)
Таким образом, уточненное решение (3.25), построенное при помощи линейной комбинации из приближенных решений задачи (3.1) (с точностью второго порядка относительно шага 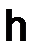 ), аппроксимирует решение
), аппроксимирует решение 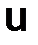 (x) дифференциальной задачи в узлах сетки
(x) дифференциальной задачи в узлах сетки 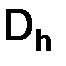 с порядком
с порядком 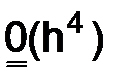 .
.
Определение. Построенный подход к получению приближенного решения более высокого порядка точности, на основе приближенных значений сеточных функций меньшего порядка точности, называется методом экстраполяции Ричардсона.
Пример (иллюстрация оценки (3.26) – результата численного эксперимента).
Рассмотрим дифференциальную задачу первого порядка
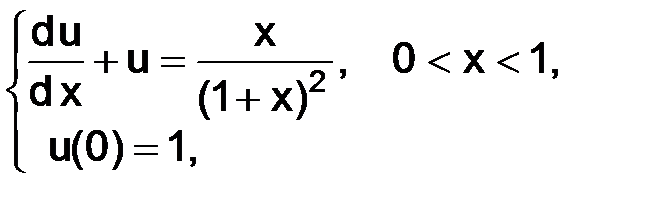
решением которой является функция: 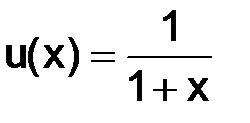 .
.
Построим сетки 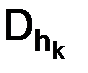 , где
, где 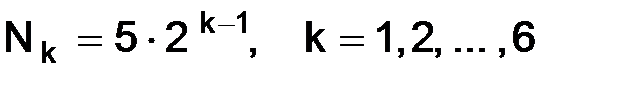 и соответствующие им разностные схемы
и соответствующие им разностные схемы 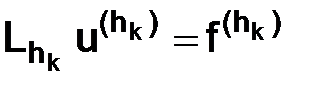 . После нахождения с помощью них приближенных решений определим величины
. После нахождения с помощью них приближенных решений определим величины 


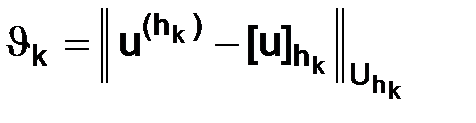 .
.
Затем на каждой сетке с шагом 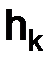 составлялась линейная комбинация из двух решений:
составлялась линейная комбинация из двух решений: 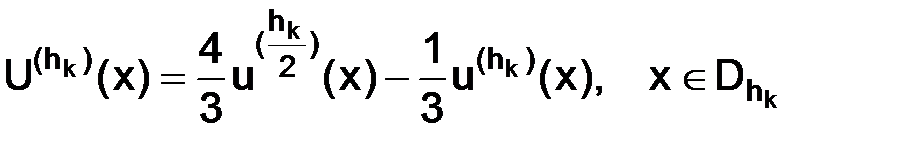 , и вновь вычислялась величина погрешности
, и вновь вычислялась величина погрешности
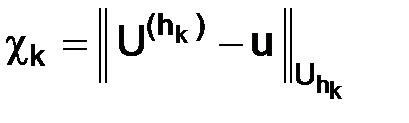 .
.
Получены следующие результаты:
1) величина погрешности не экстраполированных решений 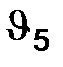
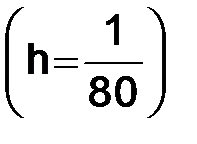 равна
равна 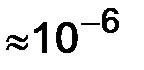 ,
, 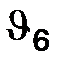
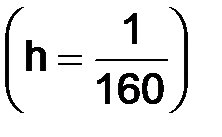
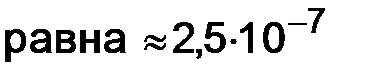 ;
;
2) величина погрешности экстраполированного решения 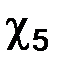
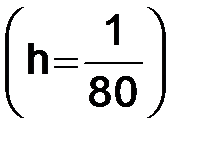 равна
равна 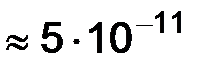 .
.
Вывод. Приведенные численные результаты показывают высокую эффективность экстраполяции Ричардсона в рассматриваемом примере.
ЗАКЛЮЧЕНИЕ
Настоящее пособие включает в себя необходимый теоретический и практический материал по теории разностных схем, предусмотренный программой подготовки специалистов вузов.
Большое внимание при изучении следует уделить прикладному характеру раздела математики. Подробное изложение учебного материала, большое количество примеров позволяют студенту самостоятельно освоить некоторые разделы программы курсов «Геометрическое моделирование в САПР» и «Модели и методы анализа проектных решений».
Авторы надеются, что овладение теорией разностных схем поможет формированию инженерного мышления будущего специалиста.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Марчук, Г.И. Методы вычислительной математики / Г.И. Марчук – М. : Лань, 2009. – 320 с.
2. Самарский, А.А. Устойчивость разностных схем / А.А. Самарский, А.В. Гулин – М. : Либроком, 2009. – 386 с.
3. Волков, Е.А. Численные методы / Е.А. Волков – М. : Лань, 2004.
– 256 с.
4. Бахвалов, Н.С. Численные методы / Н.С. Бахвалов, Н.П. Жидков, Г.М. Кобельков. – М. : МГУ, 2006. – 636 с.
5. Самарский, А.А. Введение в численные методы / А.А. Самарский.
– М. : Лань, 2009. – 288 с.
6. Романко, В.К. Разностные уравнения / В.К. Романко – М. : Бином, 2010. – 112 с.
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ............................................................................................................ 3
1. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ..................................................................................................... 4
1.1. Понятие о порядке точности и об аппроксимации............................. 4
1.1.1. Понятие о сетке и сеточной функции........................................ 4
1.1.2 Порядок точности разностной схемы........................................ 6
1.1.3. Порядок аппроксимации разностной схемы.......................... 13
1.1.4. Неустойчивая разностная схема............................................. 14
1.2. Сходимость разностной схемы........................................................... 17
1.2.1. Сходящиеся разностные схемы............................................... 17
1.2.2. Проверка сходимости разностной схемы.............................. 19
1.3. Аппроксимация дифференциальной краевой задачи
разностной схемой................................................................................ 20
1.3.1. Невязка 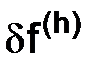 .................................................................................. 20
.................................................................................. 20
1.3.2. Вычисление невязки................................................................... 22
1.3.3. Аппроксимация порядка 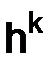 ........................................................ 24
........................................................ 24
1.4. Определение устойчивости разностной схемы.
Сходимость как следствие аппроксимации и устойчивости.......... 25
1.4.1 Определение устойчивости....................................................... 25
1.4.2. Зависимость между аппроксимацией,
устойчивостью и сходимостью.................................................. 26
1.5. Достаточный признак устойчивости разностных схем
решения задачи Коши........................................................................... 27
1.5.1. Вводный пример.......................................................................... 28
1.5.2. Каноническая запись разностной схемы................................ 30
1.5.3. Устойчивость как ограниченность норм степеней
оператора перехода.................................................................... 32
1.5.4. Пример исследования устойчивости...................................... 33
1.5.5. Схема Кранка–Николсона.......................................................... 34
1.6. Необходимый спектральный признак устойчивости....................... 37
1.6.1. Ограниченность норм степеней оператора перехода
необходима для устойчивости.................................................. 38
1.6.2. Спектральный признак устойчивости...................................... 39
2. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ
С ЧАСТНЫМИ ПРОИЗВОДНЫМИ............................................................ 41
2.1. Уравнения в частных производных и краевые задачи................... 41
2.2. Простейшие приемы построения и исследования разностных схем
для уравнений с частными производными....................................... 43
2.2.1. Построение сетки для задачи Коши........................................ 43
2.2.2. Различные разностные схемы................................................. 49
2.2.3. Метод неопределенных коэффициентов............................... 54
2.3. Некоторые основные приемы исследования устойчивости.......... 57
2.3.1. Устойчивость по начальным данным...................................... 57
2.3.2. Необходимое спектральное условие устойчивости............. 58
2.3.3. Примеры........................................................................................ 61
2.4. Разностная аппроксимация эллиптических уравнений.................. 65
2.4.1. Задача Дирихле для уравнения Пуассона
на прямоугольнике....................................................................... 65
2.4.2. Области с криволинейной границей........................................ 69
3. МЕТОД ПОВЫШЕННОЙ ТОЧНОСТИ....................................................... 70
3.1. Экстраполяция Ричардсона................................................................. 70
ЗАКЛЮЧЕНИЕ.................................................................................................... 73
БИБЛИОГРАФИЧЕСКИЙ СПИСОК................................................................ 73
Учебное издание
Рукавишников Алексей Викторович
Рукавишников Виктор Анатольевич
|
из
5.00
|
Обсуждение в статье: Что и требовалось доказать. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

