 |
Главная |
Второй способ аппроксимации граничных условий
|
из
5.00
|
Назовем совокупность узлов 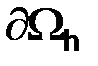 приграничными, а множество узлов
приграничными, а множество узлов  – граничными узлами сеточной области. В узлах множества
– граничными узлами сеточной области. В узлах множества 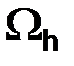 уравнение (2.34) заменим уравнением (2.40), а в узлах множества
уравнение (2.34) заменим уравнением (2.40), а в узлах множества 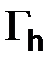 положим
положим 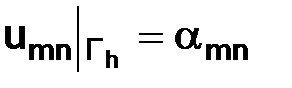 , т. е. в этом случае граничное условие выполнено точно.
, т. е. в этом случае граничное условие выполнено точно.
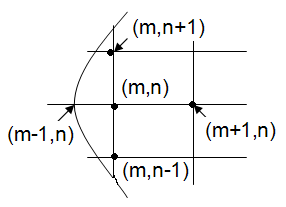 Рис. 2.12. Аппроксимация граничных условий
Рис. 2.12. Аппроксимация граничных условий
|
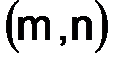 из множества
из множества 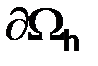 (приграничный). Для определенности будем считать, что узлы
(приграничный). Для определенности будем считать, что узлы 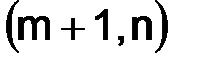 ,
, 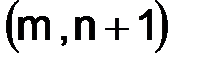 и
и  не принадлежат множеству
не принадлежат множеству 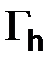 (отрезки, соединяющие их с узлом
(отрезки, соединяющие их с узлом  , принадлежат
, принадлежат  ), а узел
), а узел 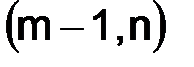 принадлежит
принадлежит 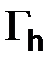 (в этом случае узел
(в этом случае узел 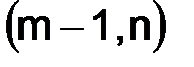 соответствует точке
соответствует точке 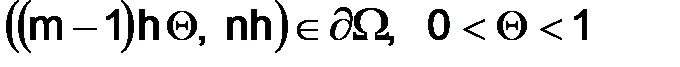 ).
).
Тогда аппроксимация (2.34) в приграничном узле (m,n) берется в виде:
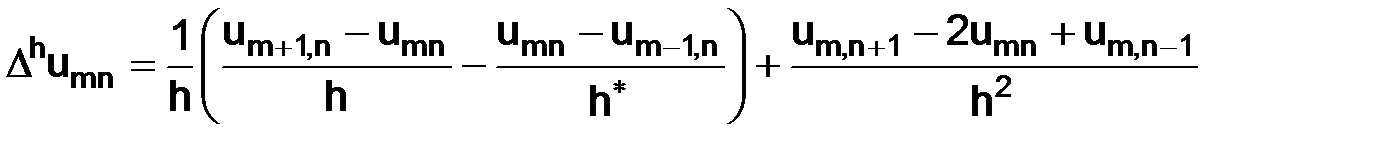 . (2.42)
. (2.42)
Здесь 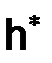 – расстояние между узлами (m–1,n) и (m,n). Аналогично поступаем и в остальных приграничных узлах
– расстояние между узлами (m–1,n) и (m,n). Аналогично поступаем и в остальных приграничных узлах  . Узлы множества
. Узлы множества  называют регулярными, а узлы множества
называют регулярными, а узлы множества  – нерегулярными. При этом:
– нерегулярными. При этом: 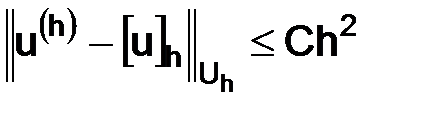 .
.
Вывод. При такой аппроксимации граничных условий, порядок сходимости приближенного решения к сеточной функции имеет тот же порядок, что и для прямоугольной области.
3. МЕТОД ПОВЫШЕННОЙ ТОЧНОСТИ
В этом разделе познакомимся с методом повышенной точности – экстраполяцией Ричардсона. Изложим схему обоснования повышенной точности экстраполированного решения и приведем численные результаты, иллюстрирующие практическую эффективность алгоритма.
3.1. Экстраполяция Ричардсона
Рассмотрим дифференциальное уравнение первого порядка
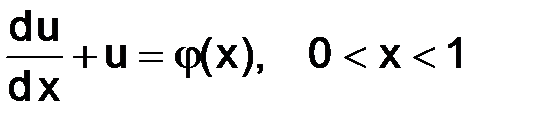 (3.1)
(3.1)
с начальным условием
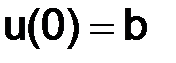 . (3.2)
. (3.2)
Предположим, что заданная функция  (x) бесконечно дифференцируема на
(x) бесконечно дифференцируема на 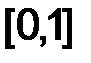 . Для численного решения задачи построим равномерную сетку
. Для численного решения задачи построим равномерную сетку 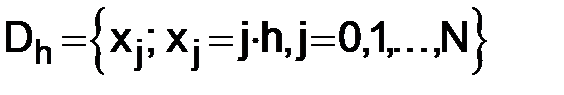 с шагом
с шагом 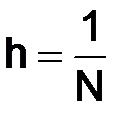 , а также введем набор средних точек, который обозначим через
, а также введем набор средних точек, который обозначим через 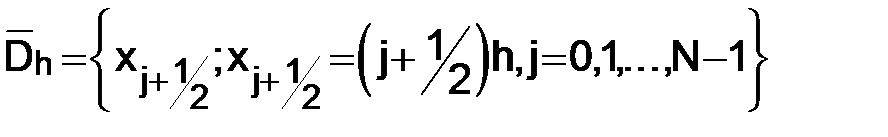 .
.
В соответствии со схемой Кранка–Николсона 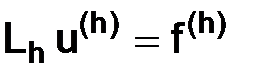 (см. п. 1.5.5) заменим уравнение (3.1) в точках
(см. п. 1.5.5) заменим уравнение (3.1) в точках 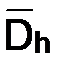 системой алгебраических уравнений, т. е.
системой алгебраических уравнений, т. е.
 (3.3)
(3.3)
где
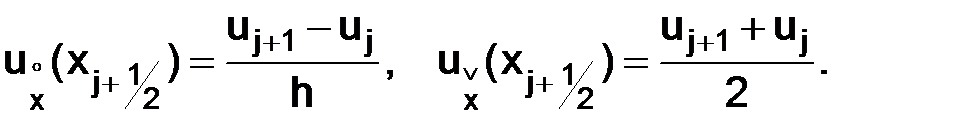
Дополним систему уравнений (3.3) условием
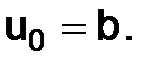 (3.4)
(3.4)
Решением задачи (3.3), (3.4) будет функция 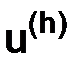 , которая приближает функцию
, которая приближает функцию 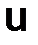 (x) со вторым порядком точности, как было показано в п. 1.5.5,
(x) со вторым порядком точности, как было показано в п. 1.5.5,
в узлах сетки 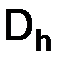 ; если
; если 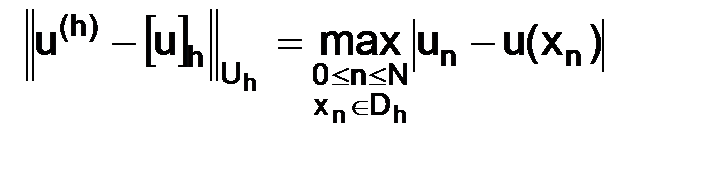 , то
, то
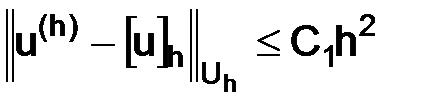 , (3.5)
, (3.5)
где 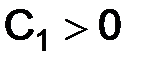 не зависит от
не зависит от 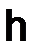 .
.
Рассмотрим погрешность решения как разность приближенного решения 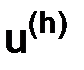 и сеточной функции
и сеточной функции 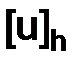 в узлах сетки
в узлах сетки 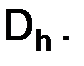
Покажем, что при  справедливо разложение
справедливо разложение
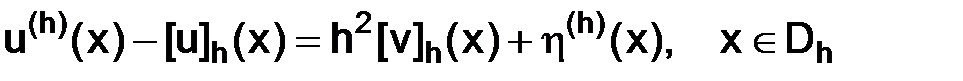 , (3.6)
, (3.6)
где 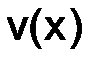 – некоторая гладкая функция, определенная на отрезке
– некоторая гладкая функция, определенная на отрезке 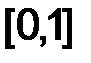 и не зависящая от
и не зависящая от 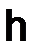 , а
, а  – функция, определенная в узлах сетки
– функция, определенная в узлах сетки 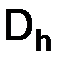 , со значениями порядка
, со значениями порядка 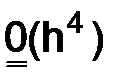 .
.
Сначала положим, что разложение (3.6) имеет место. Тогда перепишем его в таком виде
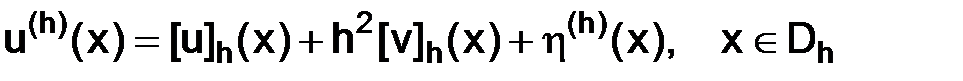 .
.
Следовательно, в узлах сетки 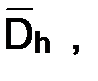 , будем иметь
, будем иметь
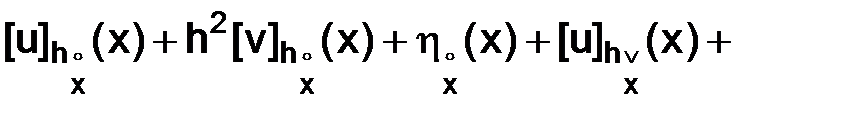
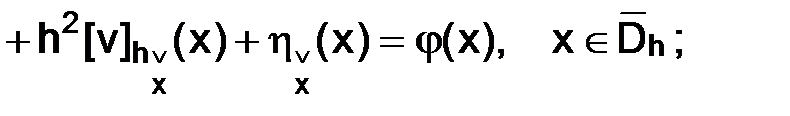 (3.7)
(3.7)
 . (3.8)
. (3.8)
Разложим в равенстве (3.7) функции 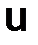 и
и  по формуле Тейлора в окрестности точки
по формуле Тейлора в окрестности точки  с остаточным членом в форме Пеано:
с остаточным членом в форме Пеано:
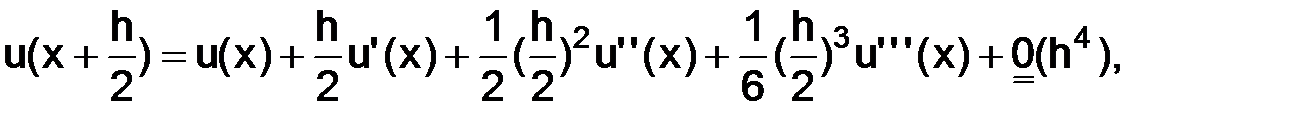
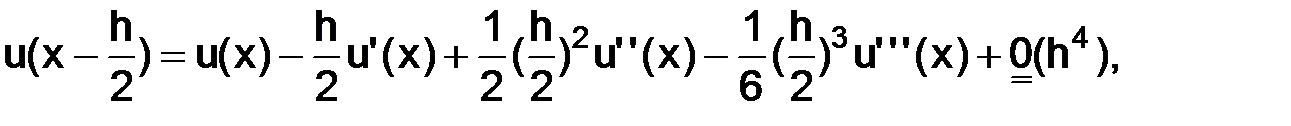

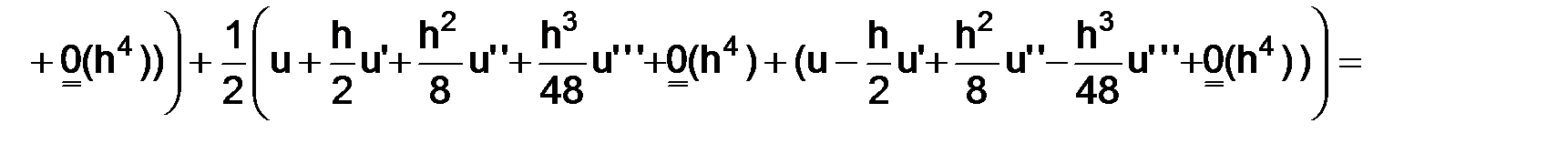
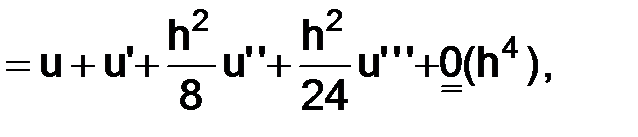
следовательно, и

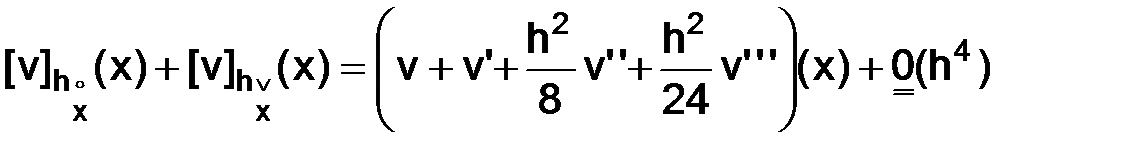 ,
,
тогда
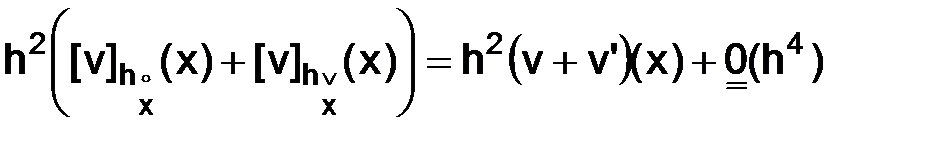 ,
,
и
 .
.
Поскольку коэффициенты при h0 и h2 не зависят от h, а остальные слагаемые в левой части предположительно имеют более высокий порядок малости (четвертый), то ввиду произвольности 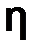 следует выполнение во всех точках сетки соотношений:
следует выполнение во всех точках сетки соотношений:
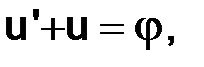 (3.9)
(3.9)
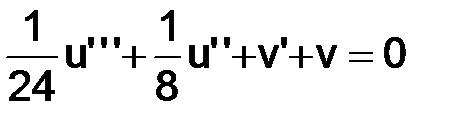 . (3.10)
. (3.10)
Аналогично рассуждая относительно (3.1.8), прейдем к тому, что
 (3.11)
(3.11)
Формулы (3.9) и (3.10) будем толковать как уравнения, которым должны удовлетворять функции 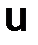 и
и  , а (3.11) как их начальные условия.
, а (3.11) как их начальные условия.
Отметим, что для функции 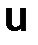 (x) эти условия выполняются автоматически, поскольку она является решением задачи (3.1), (3.2). Относительно функции
(x) эти условия выполняются автоматически, поскольку она является решением задачи (3.1), (3.2). Относительно функции  (x) получили важную информацию, которой воспользуемся в дальнейшем.
(x) получили важную информацию, которой воспользуемся в дальнейшем.
Заметим, что благодаря (3.11),  (x) – решение дифференциального уравнения
(x) – решение дифференциального уравнения
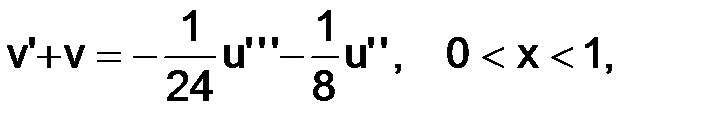 (3.12)
(3.12)
с начальным условием
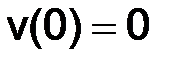 . (3.13)
. (3.13)
Задача (3.12), (3.13) разрешима, и имеет единственное решение:
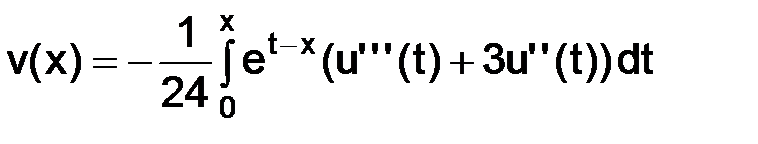 , (3.14)
, (3.14)
которое бесконечное число раз дифференцируемо по  на отрезке
на отрезке 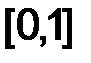 . При этом построенная функция
. При этом построенная функция  не зависит от параметра
не зависит от параметра 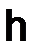 .
.
Сейчас мы покажем способ получения представления (3.14), решения дифференциального уравнения (3.12), с начальным условием (3.13).
Сделаем замену 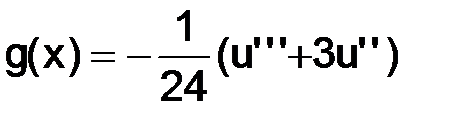 в правой части (3.12), тогда
в правой части (3.12), тогда
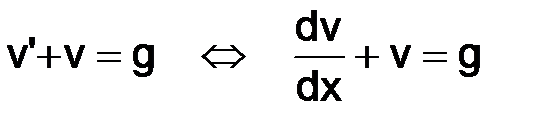 . (3.15)
. (3.15)
Решаем однородное обыкновенное дифференциальное уравнение:
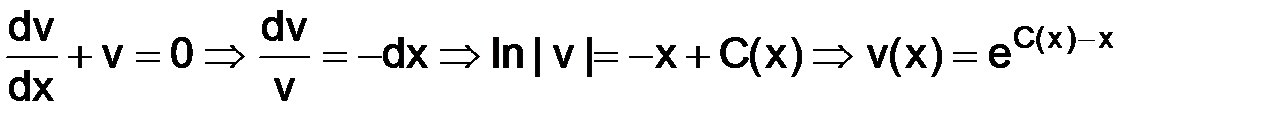 ,
,
где 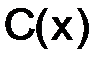 – константа, зависящая от переменной
– константа, зависящая от переменной  .
.
Следовательно, будем иметь
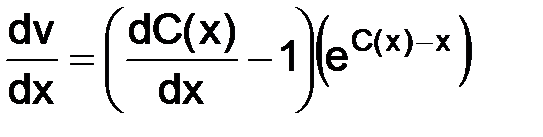 .
.
Далее, подставляем полученное для  выражение вместе с выражением для
выражение вместе с выражением для 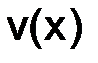 :
: 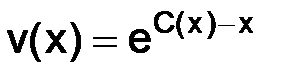 в (3.15), тогда
в (3.15), тогда 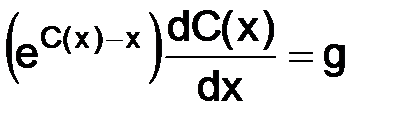 и
и 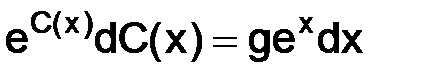 .
.
В правой части сделаем замену переменной x на  и проинтегрируем обе части от ноля до
и проинтегрируем обе части от ноля до  , получим
, получим
 ,
,
где 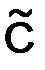 – константа, не зависящая от
– константа, не зависящая от  ; подставим
; подставим  в выражение для
в выражение для 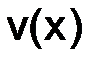 :
:
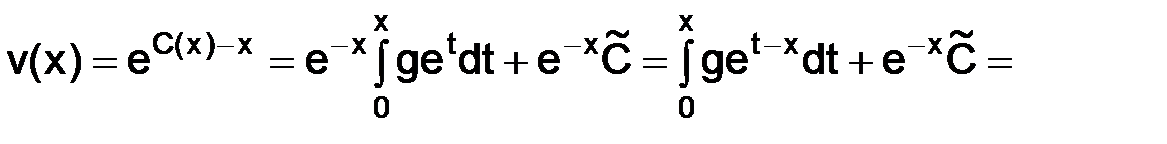
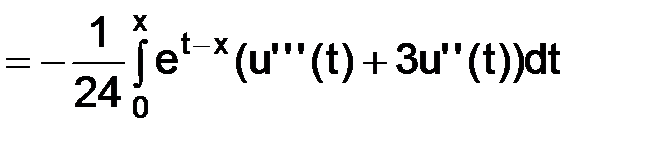 ,
,
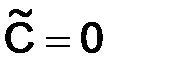 благодаря тому, что
благодаря тому, что 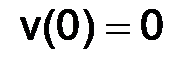 .
.
|
из
5.00
|
Обсуждение в статье: Второй способ аппроксимации граничных условий |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

