 |
Главная |
Устойчивость установлена .
|
из
5.00
|
1.5.2. Каноническая запись разностной схемы
Введем новые обозначения:
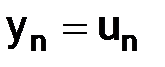 ,
, 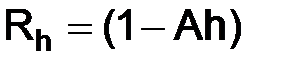 ,
, 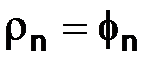 . (1.48)
. (1.48)
Равенства (1.44) (рекуррентные соотношения) запишем, используя (1.48) в виде:
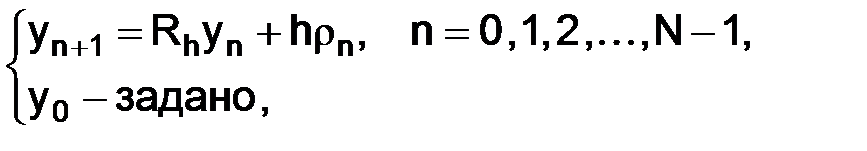 (1.49)
(1.49)
тогда представления (1.45), в обозначениях (1.48), имеют вид
 (1.45¢)
(1.45¢)
отсюда
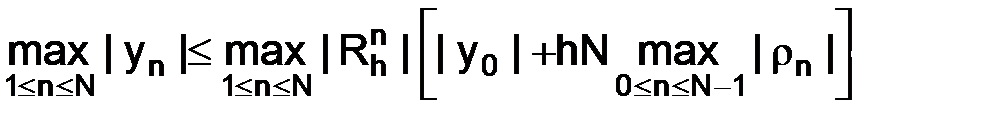 . (1.50)
. (1.50)
Далее, определим нормы
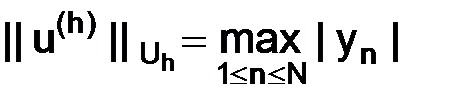 ,
, 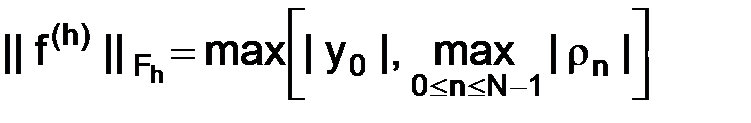 ,
,
тогда неравенство (1.50) примет вид:
 , (1.51)
, (1.51)
следовательно, для того чтобы разностная схема была устойчива, необходимо показать, что 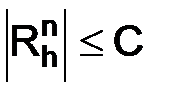 , для всех натуральных чисел
, для всех натуральных чисел 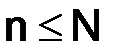 , где
, где  – некоторая положительная постоянная.
– некоторая положительная постоянная.
Вывод. Запись разностной схемы в форме (1.49) позволила свести доказательство устойчивости к получению оценки для 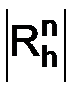 . Это удобно. Другие схемы также будем приводить к виду (1.49), который будем называть каноническим, понимая под
. Это удобно. Другие схемы также будем приводить к виду (1.49), который будем называть каноническим, понимая под 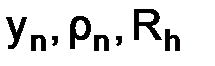 различные выражения, в каждом конкретном примере свои.
различные выражения, в каждом конкретном примере свои.
Пример. Приведем к виду  разностную схему
разностную схему 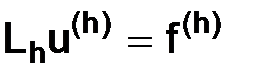 задачи (1.42):
задачи (1.42):
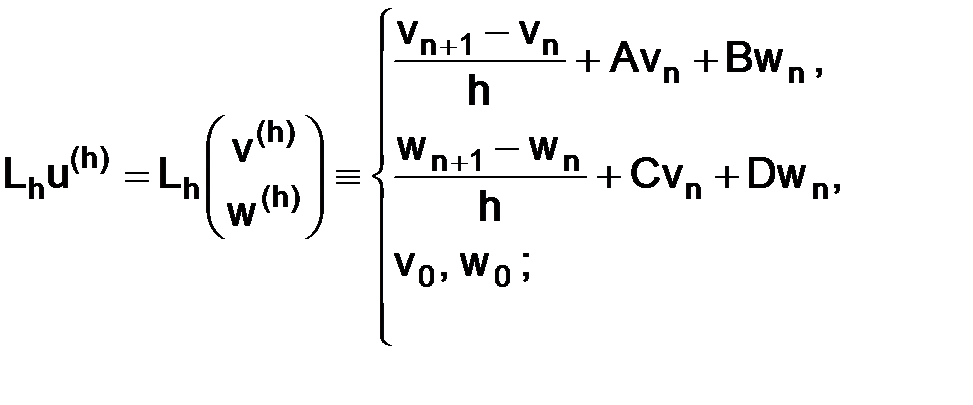
 (1.52)
(1.52)
Перепишем разностную схему (1.52) в следующем виде:

где  – матрица второго порядка (невырожденная,
– матрица второго порядка (невырожденная, 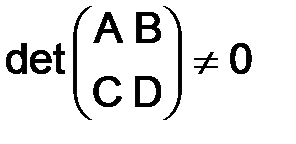 , ранг равен 2). Придадим этому векторному разностному уравнению вид рекуррентного соотношения:
, ранг равен 2). Придадим этому векторному разностному уравнению вид рекуррентного соотношения:
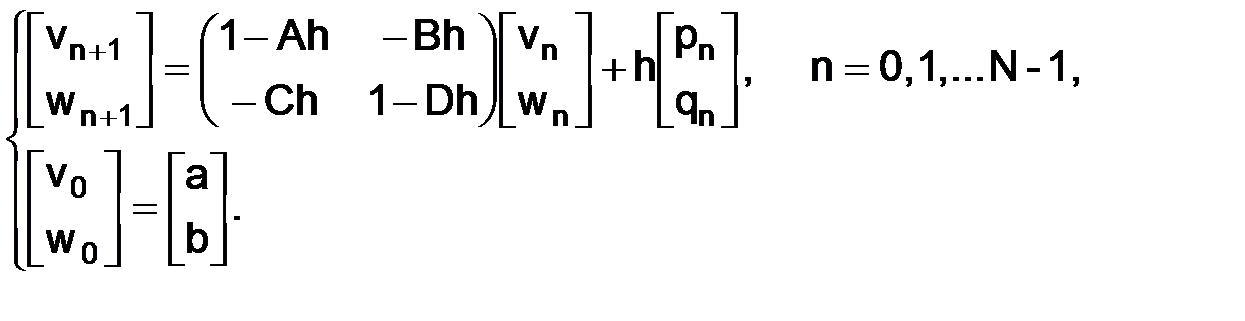 (1.53)
(1.53)
Если положить 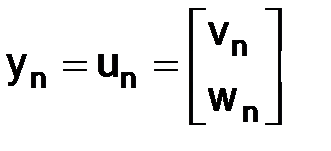 ,
, 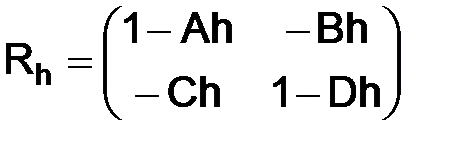 ,
, 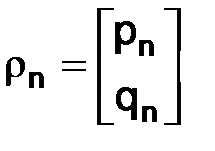 , то (1.53) приобретет требуемый вид (1.49).
, то (1.53) приобретет требуемый вид (1.49).
Сделаем отступление, а затем вернемся к этому примеру в п. 1.5.4.
1.5.3. Устойчивость как ограниченность норм степеней
оператора перехода
Сделаем замечание, которое одинаково применимо к уравнениям вида (1.49) независимо от размерности линейного пространства  , которому принадлежат векторы
, которому принадлежат векторы  и
и  , и от вида линейного оператора
, и от вида линейного оператора 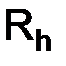 : из записи (1.49) следует запись (1.45 ¢ ).
: из записи (1.49) следует запись (1.45 ¢ ).
Если в пространстве  (
( 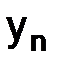 ,
, 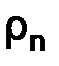
 ), введена какая-либо норма
), введена какая-либо норма  , то из равенства (1.45¢) вытекает оценка
, то из равенства (1.45¢) вытекает оценка
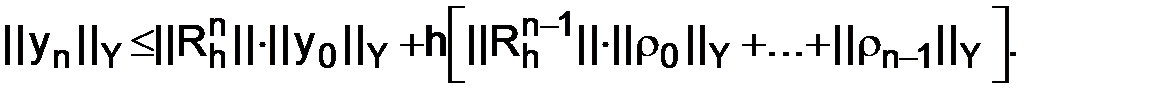 (1.54)
(1.54)
Определение. Нормой  линейного оператора Т, отображающего линейное нормированное пространство
линейного оператора Т, отображающего линейное нормированное пространство  в себя
в себя 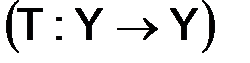 , называется число:
, называется число:
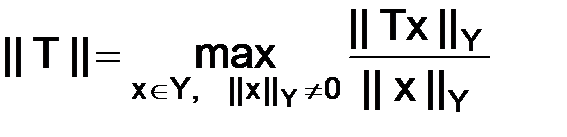 или
или 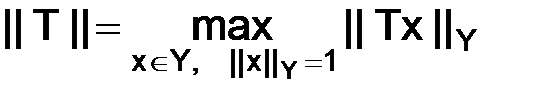 .
.
Отсюда из аксиом нормы элементов линейного пространства (см. п. 1.2.1) следует:
а)  ;
;
б) 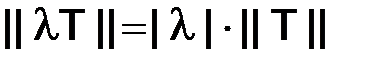 , где l – любое число;
, где l – любое число;
в) 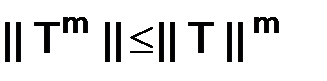 , где m – натуральное число.
, где m – натуральное число.
Задача. Проверить, используя определение нормы линейного оператора T 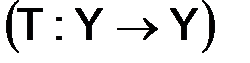 , справедливость свойств а–в.
, справедливость свойств а–в.
Первые два из этих свойств использованы для получения оценки (1.54). Из (1.54) вытекает, что
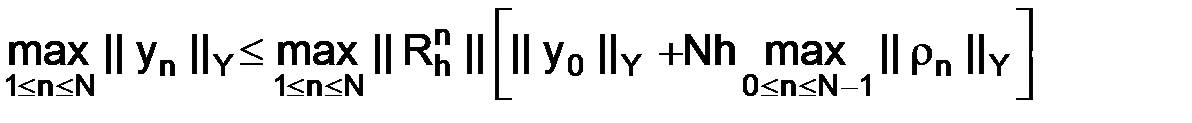 . (1.55)
. (1.55)
Утверждение. Пусть разностная схема 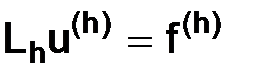 приведена к каноническому виду (1.49), и пусть нормы, введенные в пространствах
приведена к каноническому виду (1.49), и пусть нормы, введенные в пространствах 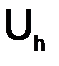 ,
, 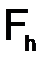 и
и  , подобраны так, что выполнены неравенства:
, подобраны так, что выполнены неравенства:
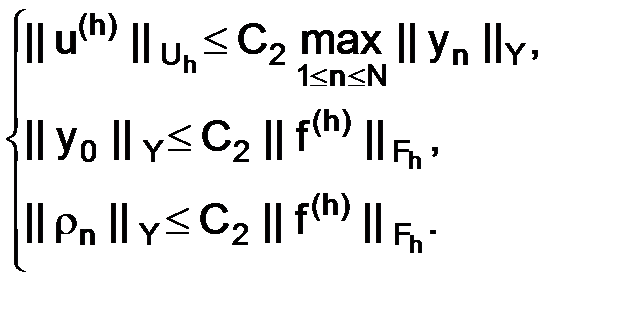 (1.56)
(1.56)
Тогда для устойчивости
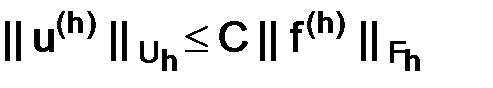 (1.57)
(1.57)
достаточно, чтобы нормы 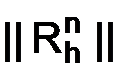 степеней оператора
степеней оператора 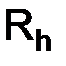 были (равномерно по
были (равномерно по  ) ограничены, т. е. чтобы выполнялось условие:
) ограничены, т. е. чтобы выполнялось условие:
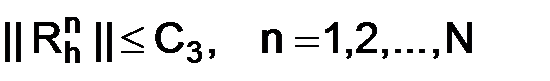 .
.
При этом, в качестве числа С, входящего в определение устойчивости (1.57), можно взять число 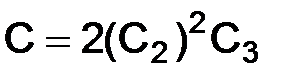 .
.
Доказательство.
Воспользуемся оценками (1.56) в условии утверждения, оценкой (1.55) и определением устойчивости разностной схемы (1.57), тогда будем иметь цепочку неравенств, которая приводит к необходимому результату утверждения
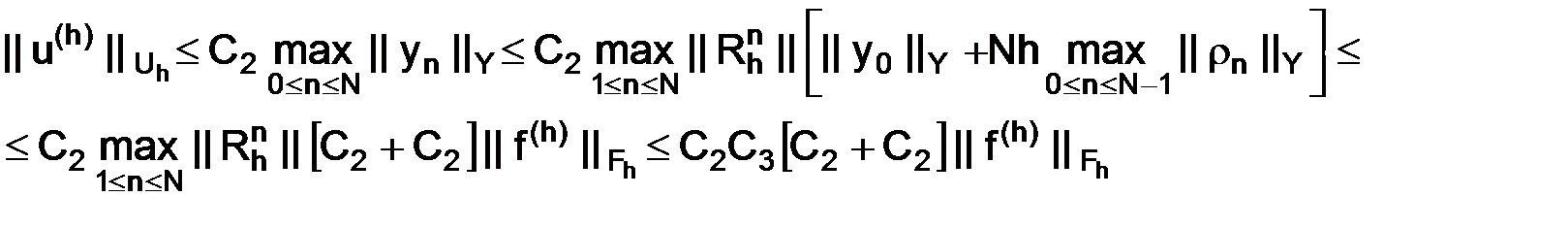
или
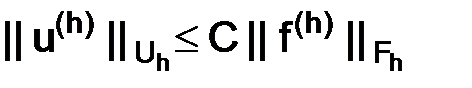 .
.
Утверждение доказано.
1.5.4. Пример исследования устойчивости
Нормы пространств 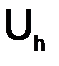 и
и 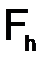 определим следующим образом:
определим следующим образом:
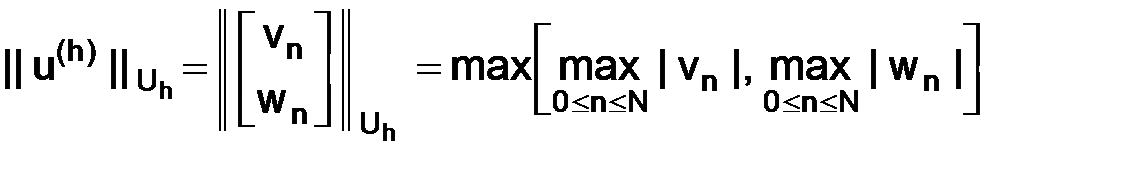 ,
,
 .
.
Имеем
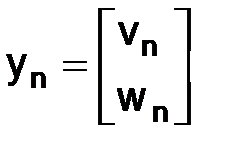 ,
,  ,
, 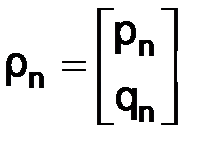 ,
, 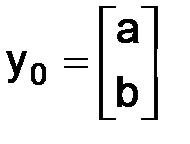 .
.
Теперь введем норму в пространстве Y, которому принадлежат векторы 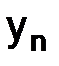 и
и 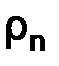 :
: 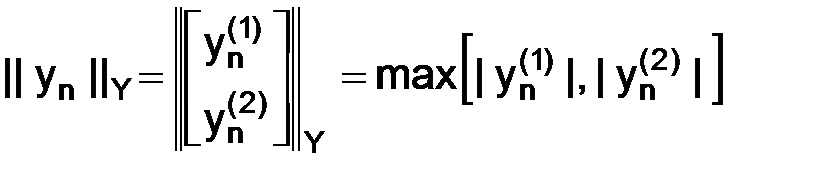 . Нормы пространств
. Нормы пространств  ,
, 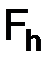 и
и  удовлетворяют условиям (1.56) утверждения предыдущего пункта. Поэтому для проверки устойчивости разностной схемы достаточно показать, что
удовлетворяют условиям (1.56) утверждения предыдущего пункта. Поэтому для проверки устойчивости разностной схемы достаточно показать, что
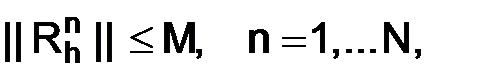
где  – положительная постоянная величина.
– положительная постоянная величина.
Заметим, что при выбранной в пространстве  норме векторов, норма соответствующего ему линейного (матричного) оператора
норме векторов, норма соответствующего ему линейного (матричного) оператора
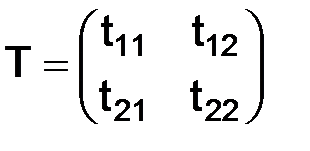
задается формулой
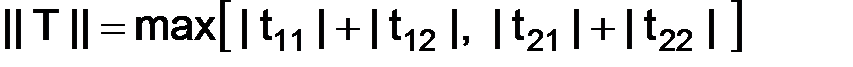 , (1.58)
, (1.58)
поскольку  достигается хотя бы при одном из двух
достигается хотя бы при одном из двух
векторов 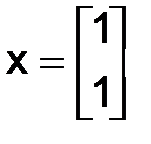 или
или  , то благодаря формуле (1.58) получим
, то благодаря формуле (1.58) получим
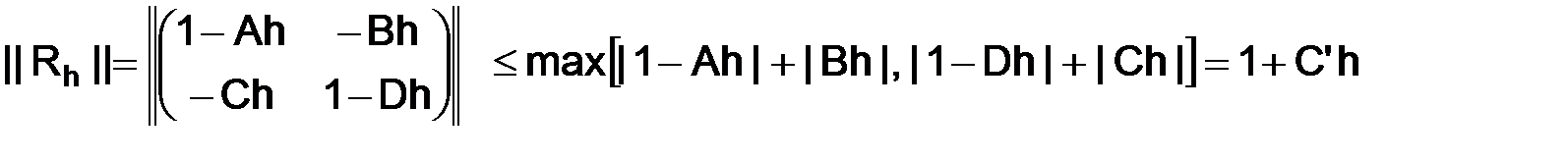 .
.
Следовательно,

для всех 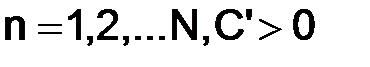 и устойчивость разностной схемы (1.52) установлена.
и устойчивость разностной схемы (1.52) установлена.
Важно.  .
.
1.5.5. Схема Кранка–Николсона
Рассмотрим задачу 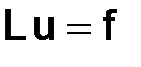 , где
, где

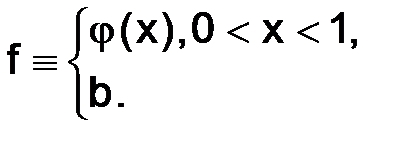 (1.59)
(1.59)
Введем норму в пространстве 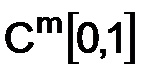 (пространстве непрерывно-дифференцируемых до m-го порядка функций на отрезке
(пространстве непрерывно-дифференцируемых до m-го порядка функций на отрезке  ):
):
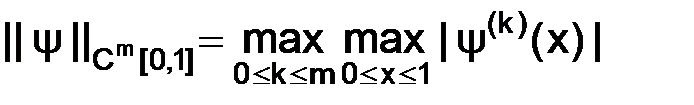 .
.
Известно, что если 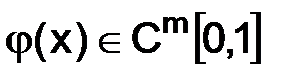 , то решение
, то решение 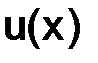 задачи (1.59) принадлежит классу функций из пространства
задачи (1.59) принадлежит классу функций из пространства  .
.
Построим сетку 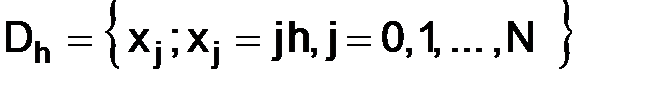 с шагом
с шагом 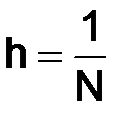 , где N – натуральное число.
, где N – натуральное число.
Введем серединные точки отрезков, соединяющих соседние точки в сетке 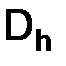 , их совокупность образует новую сетку, которую обозначим через
, их совокупность образует новую сетку, которую обозначим через  :
:
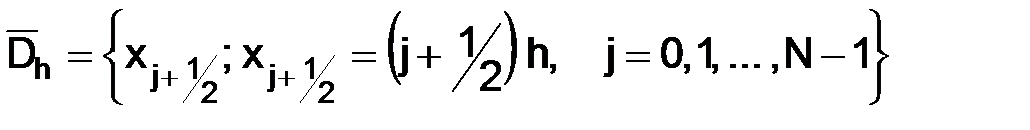
и рассмотрим разностную схему Кранка–Николсона в точках сетки 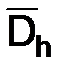 для задачи (1.59):
для задачи (1.59):
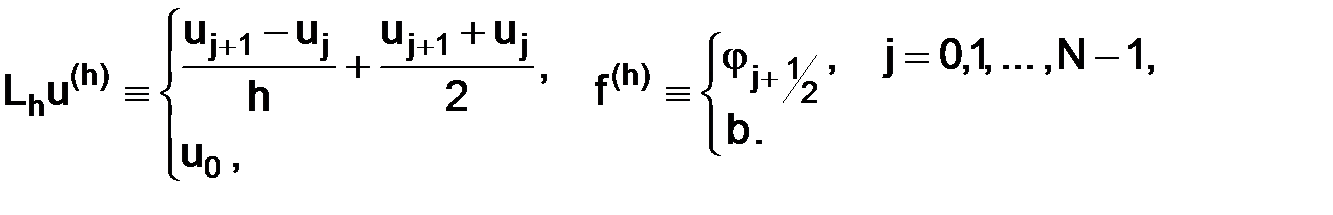
Покажем, что решение 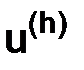 разностной краевой задачи сходится к решению
разностной краевой задачи сходится к решению 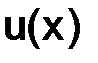 дифференциальной краевой задачи и
дифференциальной краевой задачи и
 ,
,
где константа С > 0 и не зависит от 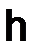 .
.
Необходимо показать:
а)  (аппроксимация порядка
(аппроксимация порядка 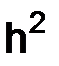 );
);
б) 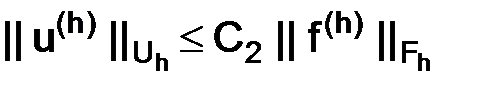 (устойчивость).
(устойчивость).
Докажем утверждение пункта а:
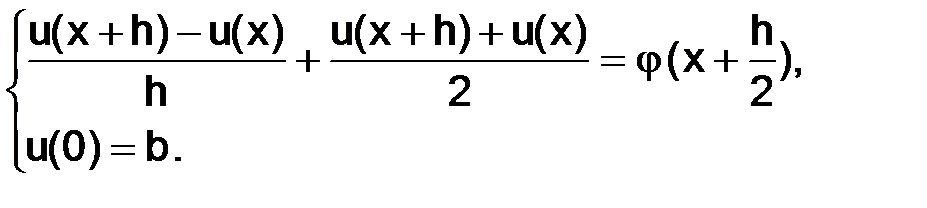 (1.60)
(1.60)
Разложим 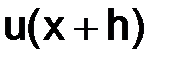 и
и 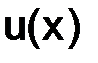 по формуле Тейлора в окрестности точки
по формуле Тейлора в окрестности точки 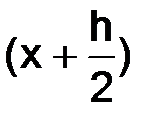 , с остаточным членом в форме Лагранжа, будем иметь
, с остаточным членом в форме Лагранжа, будем иметь
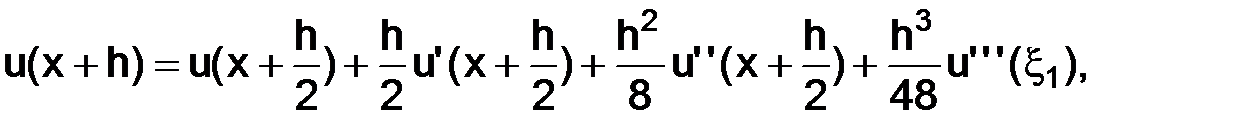
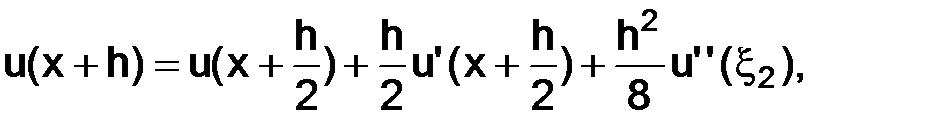
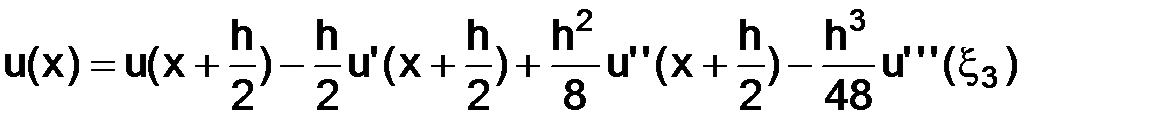 ,
,
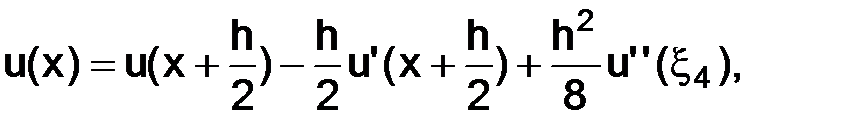
где точки  ,
, 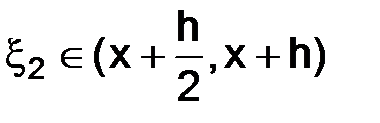 и
и  ,
, 
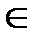
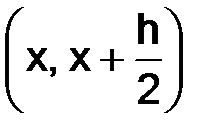 , так как
, так как
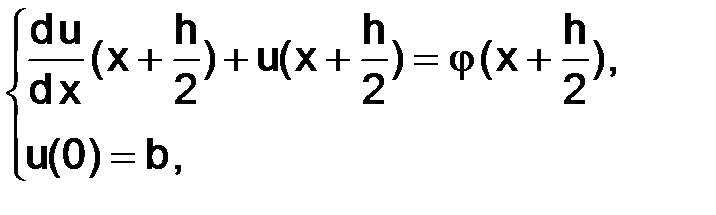
тогда, подставляя выписанные выше разложения в точках  , в (1.60), будем иметь
, в (1.60), будем иметь
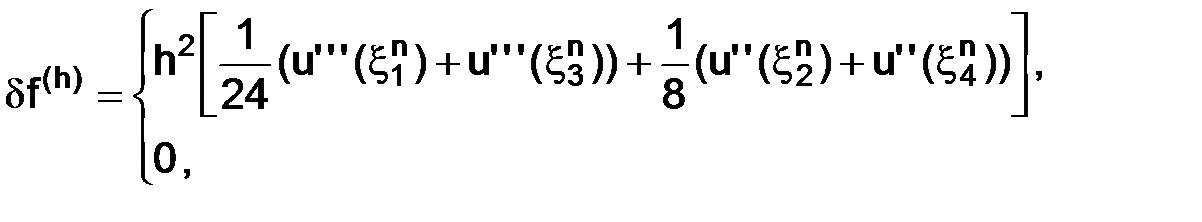
следовательно, если в пространствах 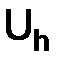 и
и 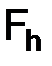 определены следующим
определены следующим
образом нормы:  ,
, 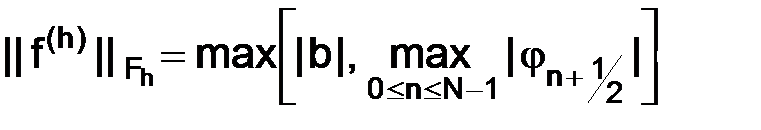 , то
, то 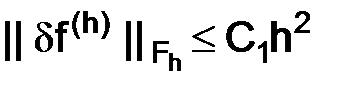 .
.
Пункт а доказан.
Докажем утверждение пункта б. Сделаем преобразование:
 ,
,
тогда
 ,
, 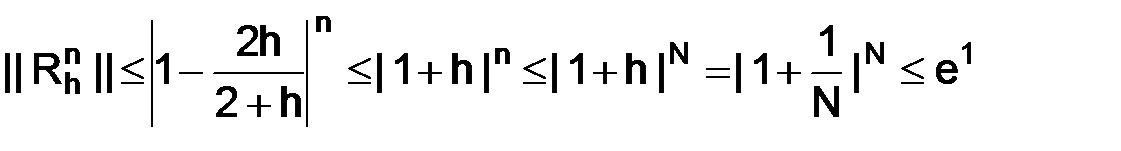 ,
,
( 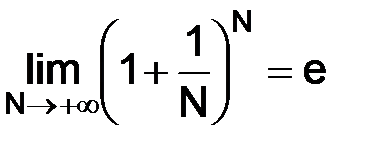 ),
), 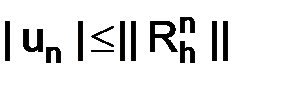
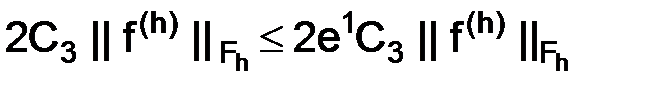 .
.
Следовательно, поскольку неравенство справедливо для любого натурального 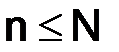 , то
, то
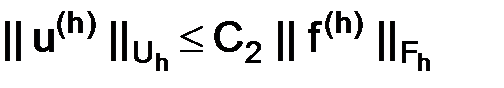 ,
,
где 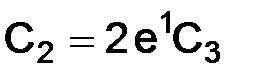 .
.
Пункт б доказан.
Вывод. Доказав пункты а и б, мы установили, что решение  разностной краевой задачи (разностной схемы Кранка–Николсона) сходится к решению
разностной краевой задачи (разностной схемы Кранка–Николсона) сходится к решению 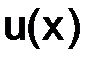 дифференциальной краевой задачи (1.59) и имеет место сходимость порядка
дифференциальной краевой задачи (1.59) и имеет место сходимость порядка 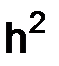 .
.
1.6. Необходимый спектральный признак устойчивости
В предыдущем пункте мы показали, что приведение разностной схемы решения задачи Коши
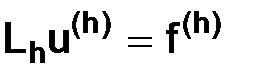 (1.61)
(1.61)
к виду
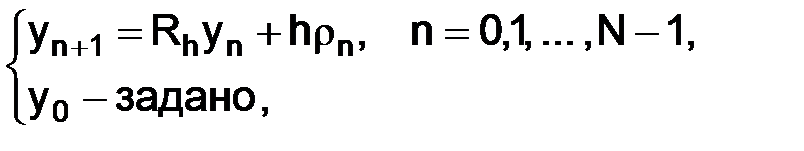 (1.62)
(1.62)
может быть использовано для доказательства устойчивости. Если выполнены условия:
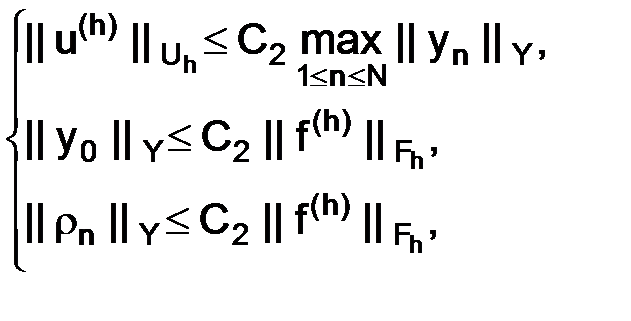 (1.63)
(1.63)
то оценка 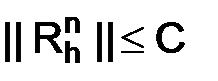 достаточна для устойчивости (1.62).
достаточна для устойчивости (1.62).
Здесь мы покажем, что эта оценка при некоторых естественных условиях необходима для устойчивости.
Покажем, что, независимо от выбора нормы, для оценки (1.62) необходимо, чтобы спектр матрицы 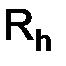 , т. е. совокупность корней уравнения (относительно
, т. е. совокупность корней уравнения (относительно  )
)
 (1.64)
(1.64)
лежал в круге
 (1.65)
(1.65)
где константа С > 0 не зависит от  ; Е – единичная матрица.
; Е – единичная матрица.
1.6.1. Ограниченность норм степеней оператора перехода
необходима для устойчивости
Отметим, что если мы приводим разностную схему (1.61) к виду (1.62) с нулевой правой частью, то значения 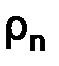 также равны нeлю.
также равны нeлю.
Пусть постоянные 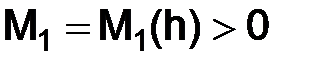 и
и 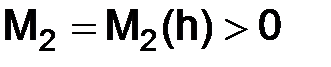 выбраны так, чтобы выполнялись неравенства:
выбраны так, чтобы выполнялись неравенства:
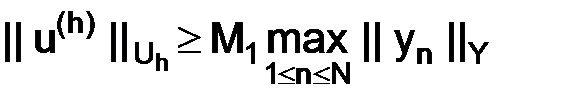 и
и 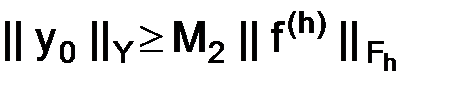 , (1.66)
, (1.66)
тогда
 и
и  , (1.67)
, (1.67)
далее, используя (1.66) и (1.67), будем иметь
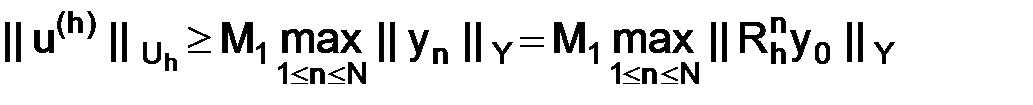 . (1.68)
. (1.68)
Из определения нормы линейного оператора (см. пункт 1.5.3) следует, что всегда из конечномерного пространства можно выбрать такой вектор 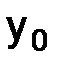 , чтобы для фиксированной натуральной степени n оператора перехода было справедливо равенство
, чтобы для фиксированной натуральной степени n оператора перехода было справедливо равенство 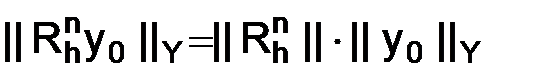 . Поэтому для этого вектора
. Поэтому для этого вектора 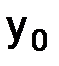 , зависящего от величины
, зависящего от величины 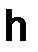 , имеет место тождество
, имеет место тождество
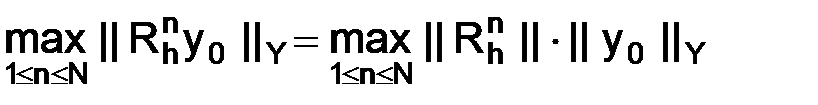 (1.69)
(1.69)
и благодаря (1.68), (1.69) и (1.66)

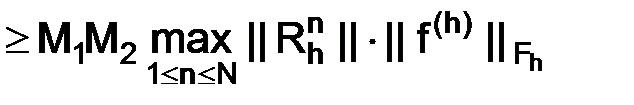 ,
,
т. е.
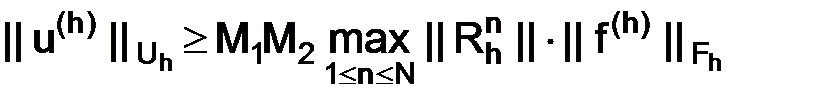 . (1.70)
. (1.70)
Из оценки (1.70) следует, что в случае устойчивости схемы (1.61) постоянная 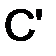 >0, входящая в определение устойчивости
>0, входящая в определение устойчивости 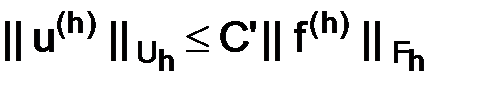 , должна удовлетворять оценке
, должна удовлетворять оценке
 ,
,
т. е.
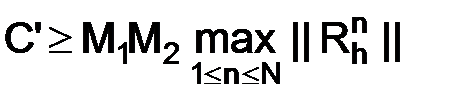 .
.
Вывод. Если нормы 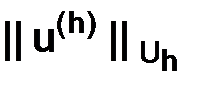 ,
, 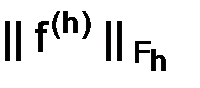 и
и 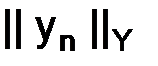 согласованы так, что выполнены условия (1.66), то условие (1.63) необходимо для устойчивости. Условие (1.63) равносильно тому, что решение
согласованы так, что выполнены условия (1.66), то условие (1.63) необходимо для устойчивости. Условие (1.63) равносильно тому, что решение 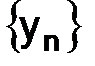 однородного уравнения
однородного уравнения 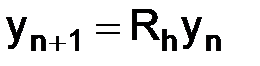 для любого
для любого  удовлетворяет неравенству
удовлетворяет неравенству
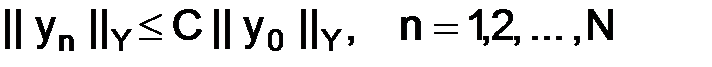 , (1.71)
, (1.71)
где  – положительная постоянная.
– положительная постоянная.
1.6.2. Спектральный признак устойчивости
Для оценки 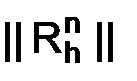 можно воспользоваться собственными значениями матрицы
можно воспользоваться собственными значениями матрицы 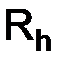 , т. е. корнями уравнения
, т. е. корнями уравнения  . Если
. Если 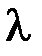 – собственное значение матрицы перехода
– собственное значение матрицы перехода  , то существует ненулевой собственный вектор
, то существует ненулевой собственный вектор  (ненулевой вектор – вектор, у которого хотя бы одна ненулевая компонента), такой, что
(ненулевой вектор – вектор, у которого хотя бы одна ненулевая компонента), такой, что 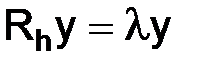 . Следовательно,
. Следовательно,
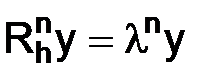 ,
, 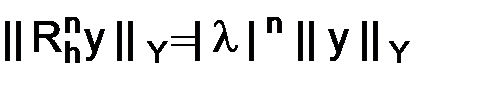 ,
, 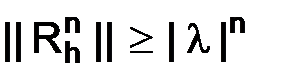 . (1.72)
. (1.72)
Таким образом, для ограниченности норм степеней оператора перехода 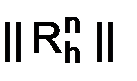 необходимо, чтобы были ограничены степени
необходимо, чтобы были ограничены степени 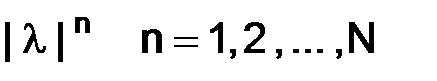 . Для этого все собственные значения должны лежать в круге радиуса
. Для этого все собственные значения должны лежать в круге радиуса  :
:
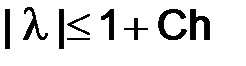 (1.73)
(1.73)
на комплексной плоскости, где С > 0 и не зависит от 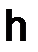 .
.
Если не выполнено (1.73), т. е.  , то для произвольного положительного числа С и некоторого достаточно малого
, то для произвольного положительного числа С и некоторого достаточно малого 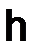 , такого, что
, такого, что 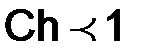 (здесь символом
(здесь символом 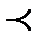 означает, что величина
означает, что величина  чуть меньше 1), справедливо
чуть меньше 1), справедливо
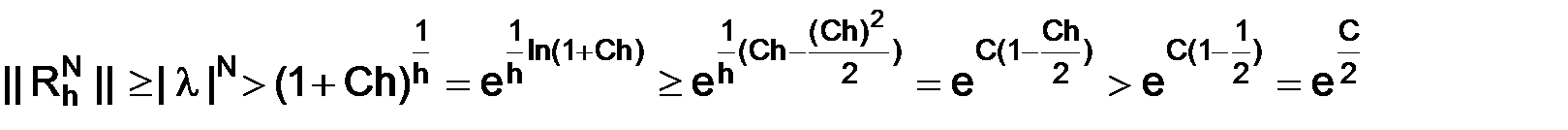
(использовали разложение по формуле Тейлора в окрестности точки ноль: 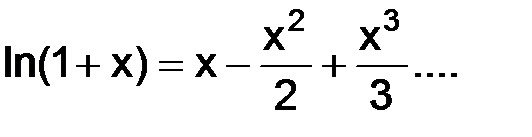 ), следовательно, будем иметь
), следовательно, будем иметь
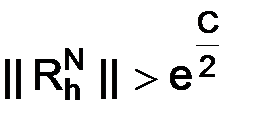 ,
,
но константа С может быть сколь угодно большой и при этом  .
.
Вывод. Сформулированный признак оценки норм степеней оператора перехода 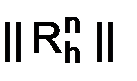 по расположению спектра (1.73) (т. е. совокупности собственных значений) оператора
по расположению спектра (1.73) (т. е. совокупности собственных значений) оператора 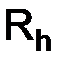 не зависит от выбора нормы в пространстве, где действует оператор
не зависит от выбора нормы в пространстве, где действует оператор 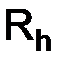 . Спектральный признак устойчивости (1.73) не зависит от способа приведения разностной схемы (1.61) к каноническому виду (1.62).
. Спектральный признак устойчивости (1.73) не зависит от способа приведения разностной схемы (1.61) к каноническому виду (1.62).
Пример. Воспользуемся необходимым спектральным признаком устойчивости (1.73) и докажем, что схема, рассмотренная в подразд. 1.1, действительно неустойчива. В подразд. 1.1 строгого исследования устойчивости не могло быть проведено, хотя бы потому, что там еще не были введены строгие определения сходимости, аппроксимации и устойчивости.
Интересующая нас разностная схема приближает дифференциальную задачу первого порядка
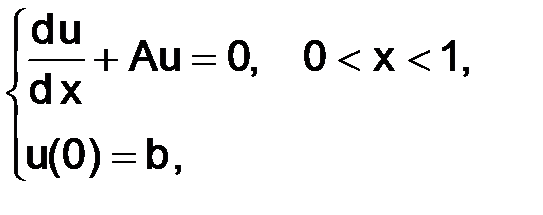
и имеет вид
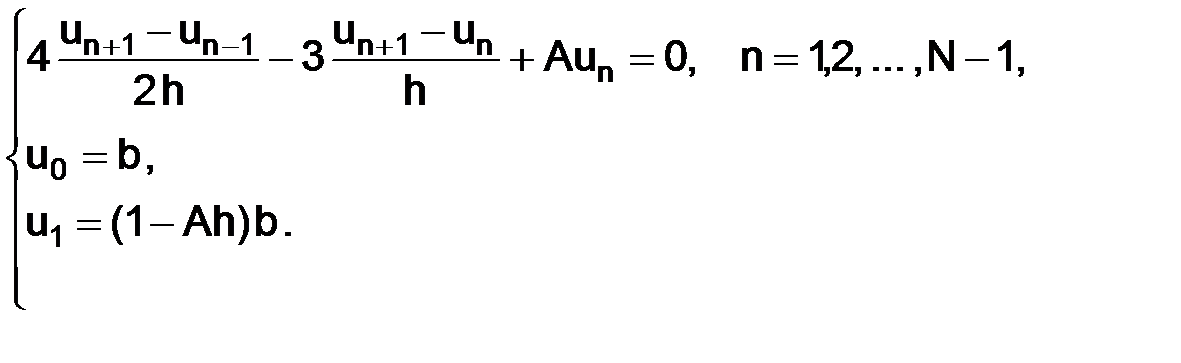 (1.74)
(1.74)
Положив 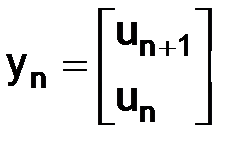 , приведем схему (1.74) к каноническому виду (1.62):
, приведем схему (1.74) к каноническому виду (1.62): 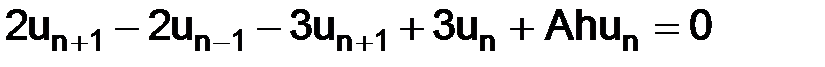 , т. е.
, т. е.  . Следовательно, и
. Следовательно, и  . Выразив
. Выразив 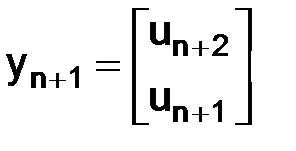 через
через 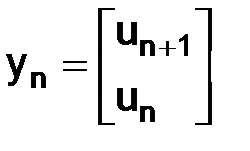 , имеем
, имеем
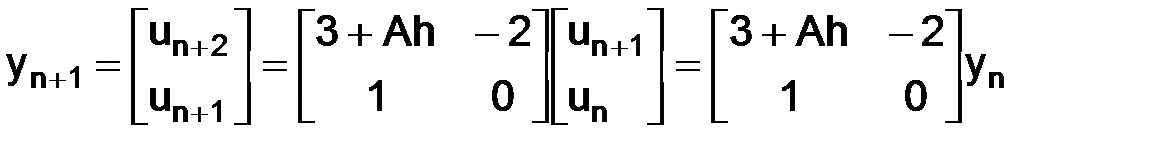 ,
,
т. е.
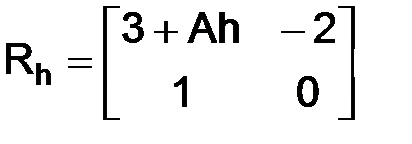 и
и 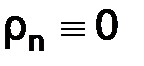 .
.
Собственные значения матрицы 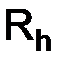 ,
, 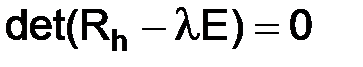 ,
, 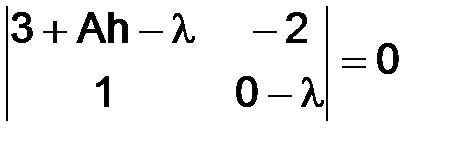 , есть корни квадратного уравнения
, есть корни квадратного уравнения 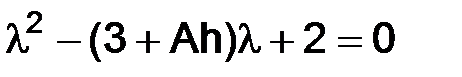 :
:
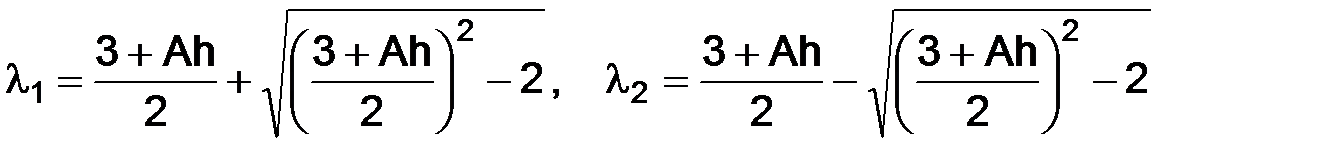 ,
,
следовательно, 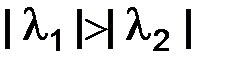 и
и 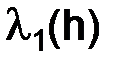 при
при 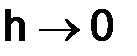 стремится к числу 2, так, что при малых
стремится к числу 2, так, что при малых 
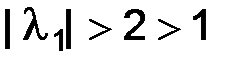 , поэтому нельзя ожидать устойчивости.
, поэтому нельзя ожидать устойчивости.
Важно. Подчеркнем, однако, что расположение спектра оператора 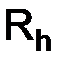 внутри круга радиуса
внутри круга радиуса 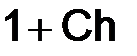 :
: 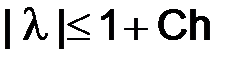 еще не гарантирует устойчивости.
еще не гарантирует устойчивости.
2. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ
С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
В этом разделе проиллюстрируем некоторые основные способы построения разностных схем и проверки их устойчивости для уравнений с частными производными. При этом обнаружится много важных и новых, по сравнению со случаем обыкновенных дифференциальных уравнений, обстоятельств.
Главные из них:
– разнообразие сеток и способов аппроксимации;
– неустойчивость большинства взятых наудачу аппроксимирующих схем;
– сложность исследования устойчивости;
– трудности вычисления решений разностных краевых задач, требующие специальных усилий для их преодоления.
2.1. Уравнения в частных производных и краевые задачи
В общем случае дифференциальное уравнение в частных производных с 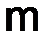 независимыми переменными можно записать в виде
независимыми переменными можно записать в виде
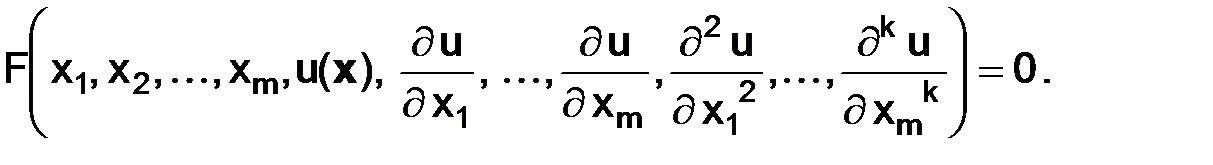
Напомним, что наивысший порядок k производной от неизвестной функции  , входящей в дифференциальное уравнение, называется его порядком. Будем рассматривать только линейные уравнения первого и второго порядка. В общем случае они соответственно записываются в виде
, входящей в дифференциальное уравнение, называется его порядком. Будем рассматривать только линейные уравнения первого и второго порядка. В общем случае они соответственно записываются в виде
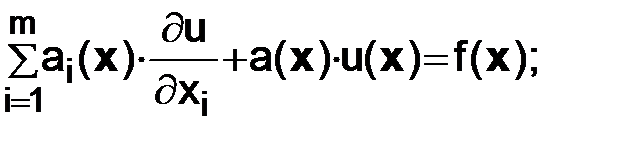 (2.1)
(2.1)
 (2.2)
(2.2)
где  – заданные функции, зависящие от переменных
– заданные функции, зависящие от переменных 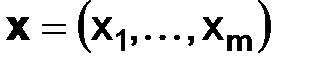 .
.
Функции 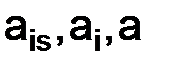 называют коэффициентами уравнения. Функция f, стоящая в правой части уравнения, называется свободным членом. Различают уравнения однородные, когда
называют коэффициентами уравнения. Функция f, стоящая в правой части уравнения, называется свободным членом. Различают уравнения однородные, когда 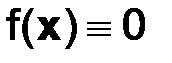 , и неоднородные в противном случае.
, и неоднородные в противном случае.
В уравнениях, связанных с физикой, независимые переменные часто суть время и пространственные переменные координаты, для их обозначения используют буквы 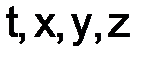 .
.
Примеры.
1. Уравнение колебания струны
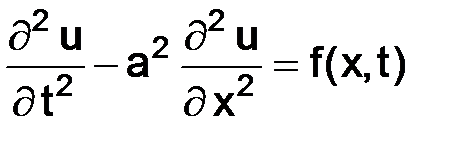 .
.
2. Уравнение Пуассона
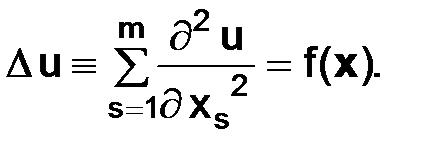 (2.3)
(2.3)
3. Уравнение Лапласа
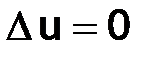 .
.
Желая полностью охарактеризовать физическую задачу, мы не можем ограничиться только дифференциальным уравнением; необходимо добавить дополнительные соотношения, которые обычно носят характер так называемых краевых (или граничных) условий.
Поясним на примере. Допустим, в теле установилось распределение температур. Если тело однородное и анизотропное, то мы приходим к уравнению (2.3), где 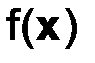 – тепловыделение. Одного уравнения (2.3) недостаточно, чтобы однозначно определить распределение температуры в теле
– тепловыделение. Одного уравнения (2.3) недостаточно, чтобы однозначно определить распределение температуры в теле  , уравнения имеют бесконечно много решений, необходима дополнительная информация. Ее можно получить, например, так. Поверхность
, уравнения имеют бесконечно много решений, необходима дополнительная информация. Ее можно получить, например, так. Поверхность 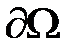 (граница) рассмотренного тела доступна для наблюдений, в любой ее точке можно измерить температуру. Пусть температура
(граница) рассмотренного тела доступна для наблюдений, в любой ее точке можно измерить температуру. Пусть температура 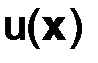 на
на 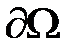 равна
равна 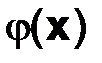 , тогда получаем дополнительное краевое условие
, тогда получаем дополнительное краевое условие
 . (2.4)
. (2.4)
Уравнение (2.3) при краевом условии (2.4) называют задачей Дирихле или первой краевой задачей.
Дополнительная информация для уравнения (2.3) может описываться не только краевым условием (2.4). Так, если известно, что в точке 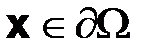 интенсивность теплового потока равна
интенсивность теплового потока равна 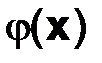 , то
, то
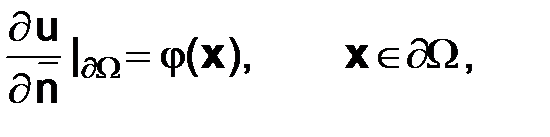 (2.5)
(2.5)
где  – вектор внешней нормали к
– вектор внешней нормали к 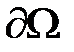 .
.
Задача (2.3), (2.5) называется задачей Неймана или второй краевой задачей.
Если для уравнения (2.3) поставлено краевое условие

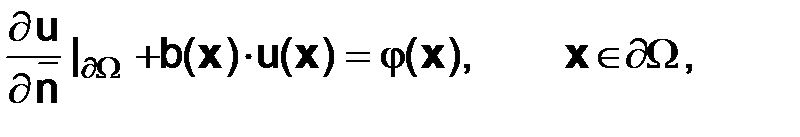 (2.6)
(2.6)
где 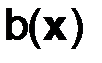 – заданная функция, то задачу (2.3), (2.6) называют третьей краевой задачей.
– заданная функция, то задачу (2.3), (2.6) называют третьей краевой задачей.
2.2. Простейшие приемы построения и исследования разностных схем для уравнений с частными производными
2.2.1. Построение сетки для задачи Коши
Отметим, что определения сходимости, аппроксимации и устойчивости имеют место (ничем не отличающиеся от определений для обыкновенных дифференциальных уравнений) для уравнений с частными производными.
Рассмотрим задачу Коши:
 (2.7)
(2.7)
Решение ищем в полосе (шириной Т) по временному слою, длина полосы по пространственной переменной бесконечность (не ограниченна).
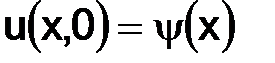 – начальное условие, в момент времени
– начальное условие, в момент времени 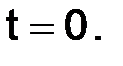
Определение. Задача, в которой решение зависит от времени, называется нестационарной задачей.
Пример нестационарной задачи – (2.7).
Определение. Задача, в которой решение не зависит от времени, называется стационарной задачей.
Пример стационарной задачи – (2.3), (2.4).
Далее, запишем задачу (2.7) в следующей форме 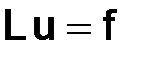 :
:
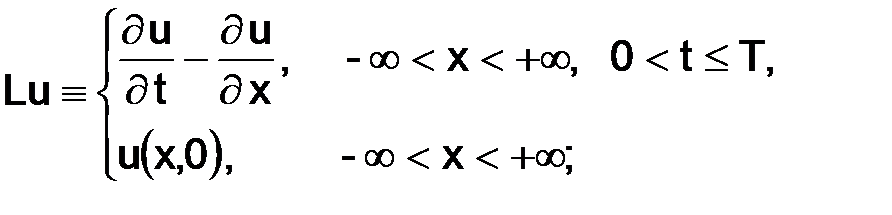
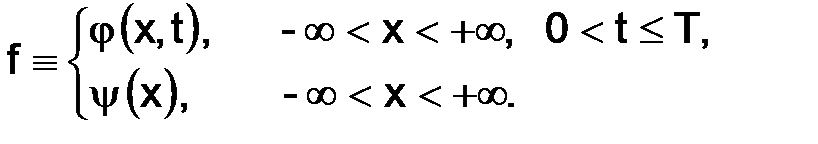
Затем построим сетку  в рассматриваемой области
в рассматриваемой области  (рис. 2.1):
(рис. 2.1): 
 числа
числа 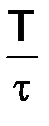 , где
, где 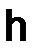 шаг по пространственной переменной
шаг по пространственной переменной  , а
, а  шаг по временной
шаг по временной
переменной  .
.
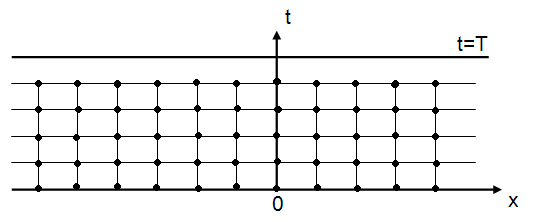
Рис. 2.1. Сетка в бесконечной полосе
Будем считать, что шаг t связан с шагом h отношением t = rh, где  положительная постоянная величина, так что сетка Dh как совокупность узлов
положительная постоянная величина, так что сетка Dh как совокупность узлов 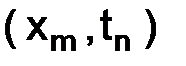 зависит только от одного параметра h (см. рис. 2.1). Искомая сеточная функция (таблица)
зависит только от одного параметра h (см. рис. 2.1). Искомая сеточная функция (таблица)  – значения решения u(x,t) дифференциального уравнения с частными производными в точках сетки Dh.
– значения решения u(x,t) дифференциального уравнения с частными производными в точках сетки Dh.
Перейдем к построению аппроксимирующей задачу (2.7) разностной схемы  . Значения функции u(h) в точках
. Значения функции u(h) в точках  сетки Dh будем обозначать через
сетки Dh будем обозначать через 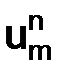 .
.
Построим разностную схему для задачи (2.7). Для этого заменим частные производные  и
и 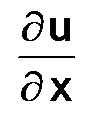 разностными отношениями в точке (x,t):
разностными отношениями в точке (x,t):
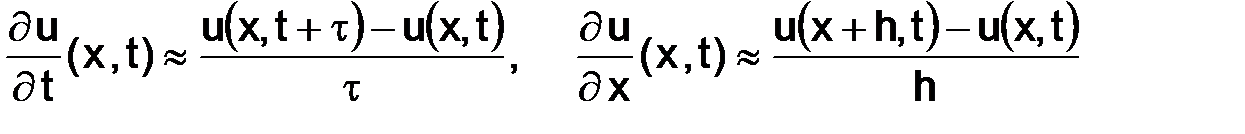 ,
,
тогда будем иметь
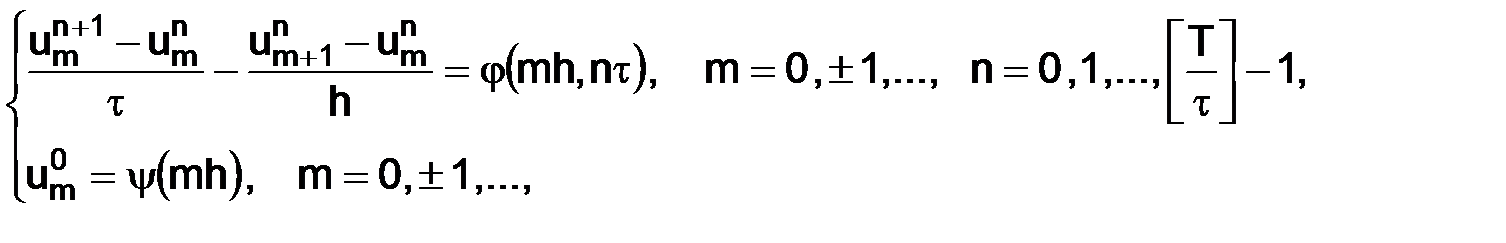 (2.8)
(2.8)
а в виде  :
:
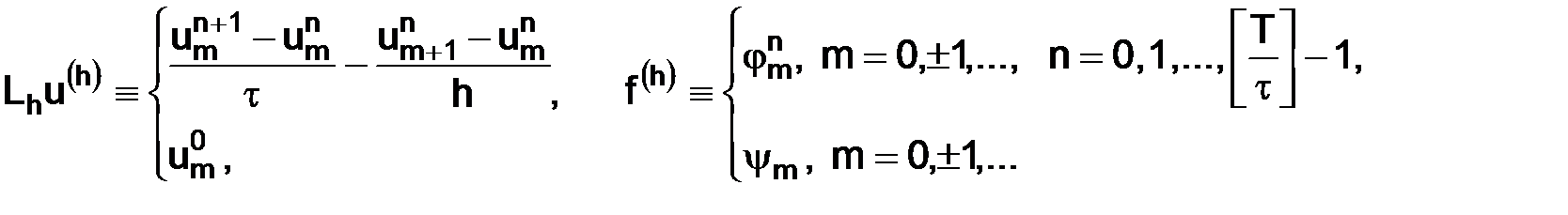
где 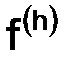 – пара функций
– пара функций 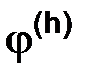 и
и 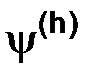 , первая задана на двумерной сетке, вторая – на одномерной (в момент времени
, первая задана на двумерной сетке, вторая – на одномерной (в момент времени 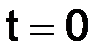 ). Разностное уравнение (2.8) можно разрешить относительно неизвестной
). Разностное уравнение (2.8) можно разрешить относительно неизвестной 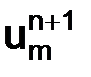 , используя соотношение
, используя соотношение 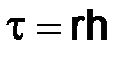 :
:
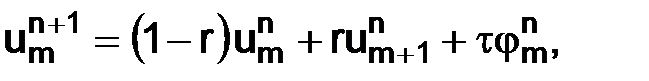 (2.9)
(2.9)
т. е., зная значения 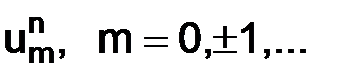 решения
решения 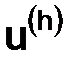 в точках сетки в момент времени
в точках сетки в момент времени 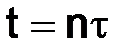 , можно вычислить значения
, можно вычислить значения 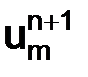 в точках сетки в момент времени
в точках сетки в момент времени  , где
, где 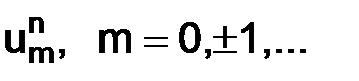 – значения на n-м временном слое.
– значения на n-м временном слое.
Поскольку известны значения на нулевом слое, т. е. 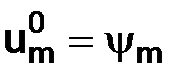 , то мы, можем вычислить значения
, то мы, можем вычислить значения 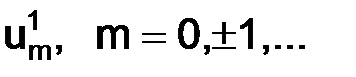 на 1-м слое, и т. д. мы можем находить значения решения
на 1-м слое, и т. д. мы можем находить значения решения  в точках сетки на прямых
в точках сетки на прямых 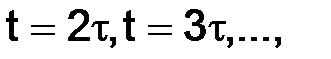 всюду на Dh.
всюду на Dh.
Перейдем к выяснению порядка аппроксимации, которым обладает схема (2.8). За Fh можно принять линейное пространство всех пар ограниченных функций 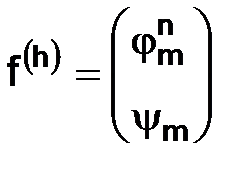 , положив
, положив
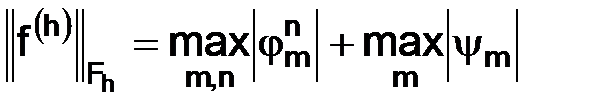 .
.
Если 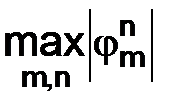 или
или 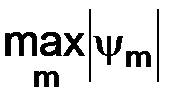 функций не достигается, то имеется в виду их точная верхняя грань:
функций не достигается, то имеется в виду их точная верхняя грань: 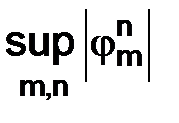 или
или 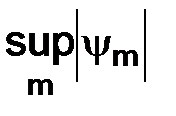 .
.
Предположим, что решение u(x,t) задачи (2.7) имеет ограниченные вторые производные по x и по t. Тогда, разложив по формуле Тейлора в окрестности точки 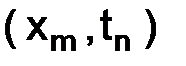 по переменным
по переменным  и
и  , с остаточными членами в форме Лагранжа, будем иметь
, с остаточными членами в форме Лагранжа, будем иметь
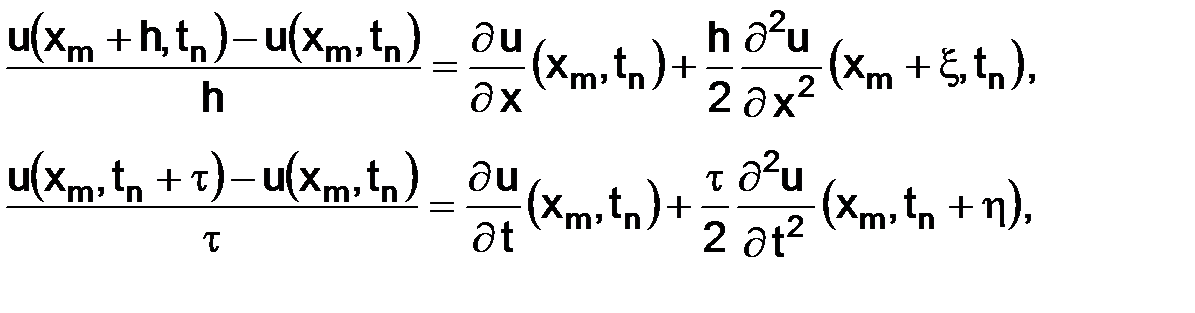 (2.10)
(2.10)
где 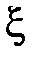 и
и 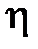 – некоторые числа, зависящие от m, n и h и удовлетворяющие неравенствам
– некоторые числа, зависящие от m, n и h и удовлетворяющие неравенствам 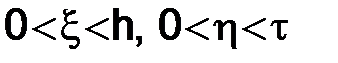 . С помощью (2.10) выражение
. С помощью (2.10) выражение
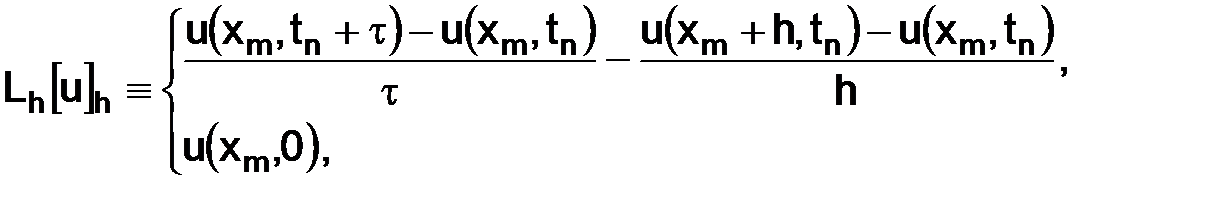
можно переписать так:

а если представить в виде
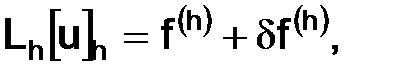
то
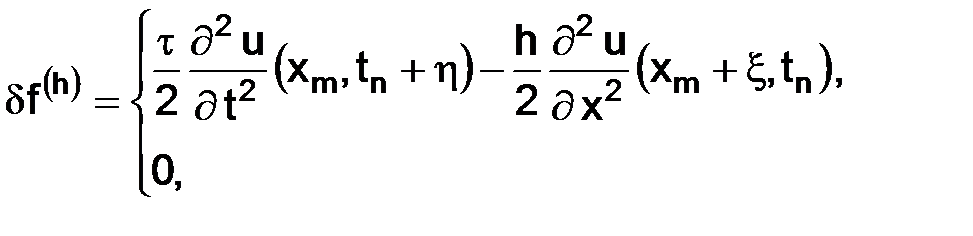
следовательно, справедлива оценка для величины невязки:
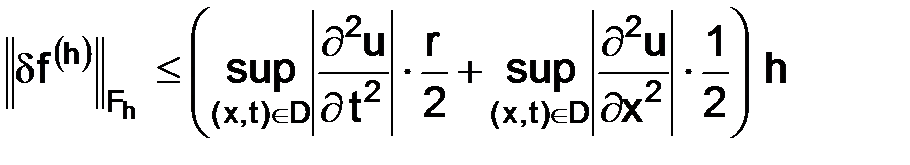 .
.
Таким образом, рассматриваемая разностная схема (2.8) имеет первый порядок аппроксимации относительно h, на
|
из
5.00
|
Обсуждение в статье: Устойчивость установлена . |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

