Дифференциальные уравнения материальной точки. Прямая и обратная задачи динамики точки.

Основные законы динамики точки.

Динамика – раздел теоретической механики, в котором изучается движение материальной точки в зависимости от сил, вызывающих это движение.

Инерциальная система координат – система координат, движущаяся поступательно, равномерно и прямолинейно относительно абсолютно неподвижной системы координат.

Законы Ньютона:

1) Изолированная материальная точка сохраняет состояние равномерного и прямолинейного движения или находится в состоянии покоя относительно инерциальной системы координат.

2) 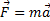 – ускорение, сообщаемое материальной точке приложенной к ней силой, по величине пропорционально силе и имеет направление этой силы. Масса материальной точки – физическая величина, являющаяся мерой инертности и гравитационных свойств.

3) Закон действия и противодействия. Силы, с которыми действуют друг на друга равны по модулю и направлены по одной прямой в противоположные стороны.

4) Закон независимости действия сил: при одновременном движении нескольких сил ускорения, сообщаемое материальной точке, равно векторной сумме ускорений, которую имела бы точка при действии каждой из сил в отдельности. ; ; ; .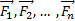

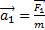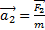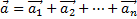Дифференциальные уравнения материальной точки. Прямая и обратная задачи динамики точки.

Ускорение материальной точки массой m, движущейся под действием сил 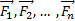, на основе закона Ньютона в векторной форме: 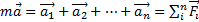. Проецируя данное уравнение на оси декартовых координат, получаем дифференциальные уравнения движения материальной точки в проекциях на оси неподвижных декартовых координат:

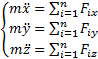 (2)   

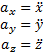
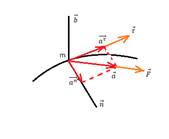Проецируя векторное уравнение на оси естественных координат, дифференциальное уравнение движения материальной точки в проекциях на оси естественных координат:

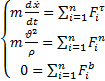 (3) ;
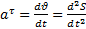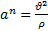
С помощью дифференциального уравнения решаются 2 основные задачи динамики: прямая и обратная. Прямой называется задача, в которой по заданному закону движения и массе материальной точки определяют равнодействующую всех сил, приложенных к этой точке.

1. Дано: m, x(t), y(t), z(t). Найти: F=?

; ; ;  → ; ; ; .

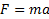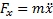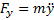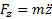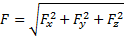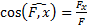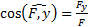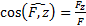2. Дано: m, S(t), 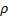. Найти: F=?

; ; ;  → .

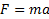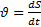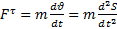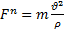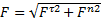Прямую задачу динамики несвободной материальной точки, в которой требуется определить активную силу или реакцию связей, решают в следующем порядке:

1) Изображаем на рисунке материальную точку в текущем положении и приложенные к ней активные силы.

2) Применив закон освобождаемости от связей, показать соответствующие реакции связей.

3) Выбрать систему отсчёта, если она не указана в условиях задачи.

4) Составить дифференциальные уравнения и определить требуемые величины.

Обратной называется задача, в которой по заданной силе и массе материальной точки определяют законы её движения.

1. Дано: m, 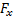, , 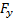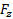. Найти: x(t), y(t), z(t)=?

2. Дано: m, 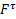, 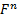. Найти: S(t)=?

Решение обратных задач динамики связано с интегрированием дифференциальных уравнений (2) и (3). Обратные задачи динамики решаются в следующем порядке:

1) Выбрать систему координат.

2) Записать начальные условия движения точек.

3) Изобразить активные силы и реакции связей.

4) Составить дифференциальные уравнения.

5) Проинтегрировать, используя начальные условия, определить постоянные интегрирования.

6) определить требуемые величины.