Приближенное решение дифференциального уравнения методом Эйлера и Рунге – Кутта.

Содержание

1.Лабораторная работа №1. Приближенное решение дифференциального уравнения методом Эйлера и Рунге – Кутта:

1.1 Теоретический материал……………………………………3

1.2 Решение уравнение методом Эйлера в MathCAD ………5

1.3 Решение уравнение методом Рунге-Кутта……………….7

Лабораторная работа №2

Приближенное вычисление определенных интегралов.

2.1 Теоретический материал………………………………………..9

2.2 Вычисление площади, ограниченную кривыми……………12

2.3 Вычисление координаты центра тяжести пластины плотности γ =1, ограниченной линиями………………………….13

Лабораторная работа №3

Разложение функций в степенной ряд. Ряд Фурье. Гармонический анализ.

3.1 Теоретический материал…………………………………………………………16

3.2 Разложение указанной функции в степенной ряд, вблизи точки x = 0………………………………………………………………………………………………………21

3.3 гармонический анализ указанной функции на отрезке [0;2 π ]…………………………………………………………………...23

Лабораторная работа № 1

Приближенное решение дифференциального уравнения методом Эйлера и Рунге – Кутта.

 

Метод Эйлера — простейший численный метод решения систем обыкновенных дифференциальных уравнений. Впервые описан Леонардом Эйлером в 1768 году в работе «Интегральное исчисление». Метод Эйлера является явным, одношаговым методом первого порядка точности. Он основан на аппроксимации интегральной кривой кусочно-линейной функцией, так называемой ломаной Эйлера..

Значение:

Метод Эйлера являлся исторически первым методом численного решения задачи Коши. О. Коши использовал этот метод для доказательства существования решения задачи Коши. Ввиду невысокой точности и вычислительной неустойчивости для практического нахождения решений задачи Коши метод Эйлера применяется редко. Однако в виду своей простоты метод Эйлера находит своё применение в теоретических исследованиях дифференциальных уравнений, задач вариационного исчисления и ряда других математических проблем.

Пусть необходимо найти решение уравнения

                                                                                                               (1)

с начальным условием . Такая задача называется задачей Коши.

Разложим искомую функцию в ряд вблизи точки и ограничимся первыми двумя членами разложения

.

Учтя уравнение (1) и обозначив , получаем

Эту формулу можно применять многократно, находя значения функции во все новых и новых точках.

                                                                                               (2)

Такой метод решения обыкновенных дифференциальных уравнений называется методом Эйлера.

 

 

Ме́тоды Ру́нге — Ку́тта — большой класс численных методов решения задачи Коши для обыкновенных дифференциальных уравнений и их систем. Первые методы данного класса были предложены около 1900 года немецкими математиками К. Рунге и М. В. Куттой.

К классу методов Рунге — Кутты относятся явный метод Эйлера и модифицированный метод Эйлера с пересчётом, которые представляют собой соответственно методы первого и второго порядка точности. Существуют стандартные явные методы третьего порядка точности, не получившие широкого распространения. Наиболее часто используется и реализован в различных математических пакетах (Maple, MathCAD, Maxima) классический метод Рунге — Кутты, имеющий четвёртый порядок точности. При выполнении расчётов с повышенной точностью всё чаще применяются методы пятого и шестого порядков точности. Построение схем более высокого порядка сопряжено с большими вычислительными трудностями.

Методы седьмого порядка должны иметь по меньшей мере девять стадий, а методы восьмого порядка — не менее 11 стадий. Для методов девятого и более высоких порядков (не имеющих, впрочем, большой практической значимости) неизвестно, сколько стадий необходимо для достижения соответствующего порядка точности^[3].

Оценку значения производной можно улучшить, увеличивая число вспомогательных шагов. На практике наиболее распространенным методом решения обыкновенных дифференциальных уравнений является метод Рунге-Кутты четвертого порядка. Для оценки значения производной в этом методе используется четыре вспомогательных шага. Формулы метода Рунге-Кутты следующие

,

,

,

,

,

.

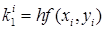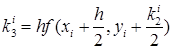Перечисленные методы можно применять и для решения систем дифференциальных уравнений. Поскольку многие дифференциальные уравнения высших порядков могут быть сведены заменой переменных к системе дифференциальных уравнений первого порядка, рассмотренные методы могут быть использованы и для решения дифференциальных уравнений порядка выше первого.

 

Задание.

1. Изучить теоретические сведения о численном решении дифференциальных уравнений.

2. Изучить способы решения дифференциальных уравнений в MathCAD.

 

 1.Решим уравнение методом Эйлера в MathCAD.

 

1) Правая часть уравнения равна:

2) Зададим границы изменения x: 

    

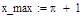
3) Зададим число точек и величину шага:

4) Зададим начальные условия:

 

5) Вычислим x и y по формулам Эйлера:

Представим результат графически и сравним его с аналитическим решением.

Аналитическое решение:

Точное аналитическое решение и решение, полученное численно, отличаются в точке x=2 на  

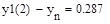
То есть относительная ошибка составляет: