 |
Главная |
Элементарные методы обработки расчетных данных
|
из
5.00
|
При изучении совокупности значений изучаемых величин, помимо средних, используют и другие характеристики. При анализе больших массивов данных обычно интересуются двумя аспектами: во-первых, величинами, которые характеризуют ряд значений как целого, т.е. характеристиками общности, во-вторых, величинами, которые описывают различия между членами совокупности, т.е. характеристиками разброса (вариации) значений.
Середина интервала возможных значений xi рассчитывается по формуле:
 ; ;
| (50) |
Мода - такое значение изучаемого признака, которое среди всех его значений встречается наиболее часто. Если чаще других встречаются два или более различных значений, такую совокупность данных называют бимодальной или мультимодальной. Если же ни одно из значений не встречается чаще других (т.е. если все значения встречаются по одному разу или равное количество раз), такая совокупность является безмодальной.
Чтобы рассчитать моду, постройте ряд данных. Слева перечислите классы с постоянными интервалами; справа частоты, соответствующие этим классам. Средний класс будет считаться классом моды, для которого вы должны отметить нижний предел и разницу в частоте для нижнего и верхнего пределов. Послемодальный класс – это следующий класс в ряду, который «выше»; заметьте разницу в частоте. Затем, чтобы найти значение моды, примените следующую формулу.
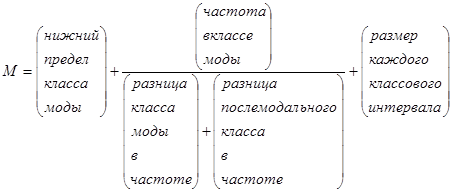
| (51) |
Пример. Определить моду по данным таблицы 27
Таблица 27
Данные для примера
| Доход за период, (руб.) Класс | Объем реализации (тыс. руб.) |
| 2000-2500 | 100,0 |
| 3000-3500 | 120,0 |
| 3000-3500 | 150,0 |
| 2500-3000 | 130,0 |
| 2200-2700 | 100,0 |
Классы (категории дохода за период) ранжированы так, что наиболее часто встречающееся значение находится в середине. Это модальный класс. Поскольку каждый класс должен иметь постоянный интервал, данный необходимо разбить на два класса 3,000 – 3,500; класс, где частота больше, был выбран модальным.
Интервал класса составляет 500. Нижний предел модального класса - 3000, разница между нижней и верхней частотами равна 30 (150,0 – 120,0). Послемодальный класс – 2500 - 3000, а разница между нижней и верхней частотами равна 20 (150,0 – 130,0).

Значение модального дохода равно 3300.
Медиана – такое значение изучаемой величины, которое делит изучаемую совокупность на две равные части, в которых количество членов со значениями меньше медианы равно количеству членов, которые больше медианы. Медиану можно найти только в совокупностях данных, содержащих нечетное количество значений. Только тогда и слева, и справа от медианного значения будет одинаковое число членов.
Пример. Рассмотрим данные по категориям объема реализации и количеству организаций в каждой категории.
Таблица 28
Данные для примера
| Реализация, тыс. руб. | Количество организаций | Кумулятивная частота |
| 0-199 | 40 | 40 |
| 200-299 | 60 | 100 |
| 300-399 | 100 | 200 |
| 400-499 | 100 | 300 |
| 500-599 | 100 | 400 |
| 600 и выше | 80 | 480 |
| 480 |
Классовые интервалы – это пределы объема реализации в левой колонке.
Количество организаций в каждом классе – это частота (средняя колонка). В правой колонке находятся кумулятивные частоты; к каждой новой частоте добавляется сумма предыдущих. Классом медианы является 400.0 – 499.0, потому что средний показатель в колонке. Его средний предел – 400.0, а интервал – 100. Кумулятивная частота до класса медианы – 200, а общая кумулятивная частота (общее количество во всех классах) равна 480.

Медиана реализации для этого ряда равна 440000.
В качестве показателей размаха и интенсивности вариации показателей чаще всего используются следующие величины: размах вариации, среднее линейное отклонение, среднеквадратическое отклонение, дисперсия и коэффициент вариации.
Размах вариации рассчитывается по формуле:
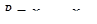 ; ;
| (52) |
Среднее линейное отклонение (средний модуль отклонения) от среднего арифметического исчисляется по формуле:
 ; ;
| (53) |
Если используются весовые коэффициенты, то формула средневзвешенного среднего линейного отклонения имеет вид:
 ; ;
| (54) |
где wi – частота, с которой в изучаемой совокупности встречается значение xi.
Пример. Рассмотрим пример расчета среднего линейного отклонения по исходным данным, приведенным в таблице 29.
Таблица 29
Распределение фирм по оснащенности работников промышленно – производственными основными фондами
Группа фирм по величине ППОФ на одного работника, тыс. руб.

| Число фирм, % к итогу

| Середина интервалов

|  
|  
|  
|
| До 1,0 | 7,8 | 0,5 | 3,9 | 6,16 | 48,048 |
| 1,1-2,0 | 12,2 | 1,5 | 18,3 | 5,16 | 62,952 |
| 2,1-3,0 | 14,9 | 2,5 | 37,25 | 4,16 | 61,984 |
| 3,1-5,0 | 23,3 | 4,0 | 93,2 | 2,66 | 61,078 |
| 5,1-10,0 | 24,3 | 7,5 | 182,25 | 0,84 | 20,412 |
| 10,1-20,0 | 10,6 | 15,0 | 159 | 8,34 | 88,404 |
| 20,1 и более | 6,9 | 25,0 | 172,5 | 18,34 | 126,56 |
| Итого | 100 | 666,4 | 470,324 |
Алгоритм расчета среднего взвешенного линейного отклонения.
1.Принимаем середины интервалов столбца А за варианты признака и определяем их значение хi′.
2. Находим произведение середин интервалов на их веса xiwi, в итоге получаем значение 666,4.
3. Рассчитываем среднее значение показателя по формуле средней арифметической взвешенной
 тыс. руб.
тыс. руб.
1. Определяем значение величины 
2. Рассчитываем произведение 
 , в результате получим значение 470, 324
, в результате получим значение 470, 324
3. Рассчитываем взвешенное среднее линейное отклонение
 тыс. руб.
тыс. руб.
Среднее линейное отклонение позволяет определить обобщенную характеристику колеблемости признака в совокупности, однако при его исчислении приходится иметь дело с модулями алгебраических выражений, что при упрощенных конечных выражениях может приводить к ошибкам и неточностям.
Более удобно использовать показатели вариации, найденные с использованием вторых степеней отклонений.
Полученная при этом мера вариации называется дисперсией (σ2), а корень квадратный из дисперсии – средним квадратическим отклонением (σ).
Дисперсия - средняя величина квадратов отклонений индивидуальных значений признака от их средней величины.
Рабочие зависимости для расчета дисперсии имеют вид:
а) простая дисперсия для не сгруппированных данных:
 ; ;
| (55) |
б) взвешенная дисперсия для интервального вариационного ряда:
 ; ;
| (56) |
Среднеквадратическое отклонение – корень квадратный из дисперсии.
а) простое среднеквадратическое отклонение для не сгруппированных данных:
 ; ;
| (57) |
б) взвешенное среднеквадратическое отклонение для интервального вариационного ряда:
 ; ;
| (58) |
Среднеквадратическое отклонение выражается в тех же единицах измерения, что и значение признака.
Величина среднеквадратического отклонения, как следует из ее определения, зависит от абсолютных значений самого изучаемого признака. Чем больше величины xi, тем больше будет σ. Поэтому для сравнения рядов данных, отличающихся по абсолютным величинам, вводят коэффициент вариации:
 ; ;
| (59) |
Этот коэффициент является показателем "количественной" неоднородности совокупности данных. Критическое значение его считается равным 33%. Если Vаr > 33%, то совокупность нельзя признать однородной.
Индексный метод
Мощным орудием сравнительного анализа экономики являются индексы. Индекс – это статистический показатель, представляющий собой отношение двух состояний какого – либо признака. С помощью индексов проводятся сравнения с планом, в динамике, в пространстве. Индекс называется простым (синонимы: частный, индивидуальный), если исследуемый признак берется без учета связи его с другими признаками изучаемых явлений. Простой индекс имеет вид:
 ; ;
| (60) |
где p1 и p0 – сравниваемые состояния признака.
Индекс называется аналитическим (синонимы: общий, агрегатный), если исследуемый признак берется не изолированно, а в связи с другими признаками. Аналитический индекс всегда состоит из двух компонент: индексируемый признак р (тот, динамика которого исследуется) и весовой признак q. С помощью признаков-весов измеряется динамика сложного экономического явления, отдельные элементы которого несоизмеримы. Простые и аналитические индексы дополняют друг друга.
 ; ;
| (61) |
где q0 или q1 – весовой признак.
С помощью индексов в анализе финансово-хозяйственной деятельности решаются следующие основные задачи:
– оценка изменения уровня явления (или относительного изменения показателя);
– выявление роли отдельных факторов в изменении результативного признака;
– оценка влияния изменения структуры совокупности на динамику.
Пример. Выручка, полученная организацией от производства и реализации продукции, может рассчитываться как цена, умноженная на физический объем реализуемой продукции.
В первом квартале реализовано 12 тыс. единиц продукции при средней цене 2400 руб. Показатели второго квартала - 11 тыс. единиц при цене 2500 руб.

Вывод: вследствие сокращения физического объёма производства и реализации на 8,3% и увеличения цены на 4,1% выручка сократилась на 4,5%.
Пример. Предприятие выпускает два вида продукции –“А” и “Б”, имеющие разные цены. Индекс выручки в этом случае будет иметь вид:
 ; ;
| (62) |
Такой индекс нельзя представить в виде произведения субиндексов (индексов факторов), как это было сделано ранее. В этом случае поступают иным образом:
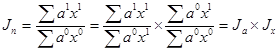 ; ;
| (63) |
Субиндекс  характеризует влияние фактора а;
характеризует влияние фактора а;
Субиндекс  характеризует влияние фактора х;
характеризует влияние фактора х;
Индекс может быть представлен в несколько ином виде:
 ; ;
| (64) |
Возникает вопрос: какой из вариантов правильно отражает влияние факторов?
Объективного ответа на этот вопрос нет. Применяется следующий подход. Если экономический показатель является произведением качественного и количественного факторов, то
а) при определении влияния количественного фактора качественный фактор фиксируется на базисном уровне;
б) при определении влияния качественного фактора количественный фактор фиксируется на новом уровне.
Если показатель является функцией двух факторов, то качественным считается тот, который является характеристикой единицы совокупности, а количественным тот, который является характеристикой всей совокупности.
Пример. Цена - характеристика единицы продукции, следовательно это качественный показатель. Объем продукции - характеристика всей совокупности. Следовательно это количественный показатель.
Тогда правильной будет следующая подстановка:
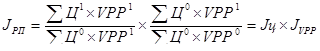 ; ;
| (65) |
Таблица 30
Данные для примера
| Вид продукции | 1 квартал | 2 квартал | ||
| Ц | VРП | Ц | VРП | |
| А | 1800 | 10 | 2000 | 8 |
| Б | 2800 | 2 | 3000 | 3 |

Вопросы для самопроверки
1. Что понимается под факторным анализом?
2. Что такое детерминированный и стохастический факторный анализ?
3. Что такое моделирование факторных систем?
4. Какие типы факторных систем бывают?
5. Какие типы сравнений применяются в анализе?
6. Каковы основные виды относительных величин?
7. В чем сущность и каковы виды средних величин?
8. В чем сущность структурных и аналитических группировок?
9. Для чего используют приемы корреляционного анализа?
10. В чем сущность индексного метода в анализе?
|
из
5.00
|
Обсуждение в статье: Элементарные методы обработки расчетных данных |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

