 |
Главная |
Задания для самостоятельного решения.
|
из
5.00
|
Ю.С.Налбандян
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к практическим занятиям по курсу
«Введение в математический анализ»
(специальность «Зарубежное регионоведение»)
Часть 1.
Элементы линейной алгебры и аналитической геометрии
Ростов-на-Дону
2012
Методические указания разработаны кандидатом физико-математических наук, доцентом кафедры математического анализа Ю.С.Налбандян
Ответственный редактор канд. физ.-матем. наук Д.А.Абанина
Компьютерный набор и верстка канд. физ.-матем. наук Ю.С.Налбандян
Печатается в соответствии с решением кафедры математического анализа факультета математики, механики и компьютерных наук, протокол № 6 от 24 апреля 2012 года.
© Ю.С.Налбандян, 2012
ВВЕДЕНИЕ
Курс «Введение в математический анализ», который читается студентам отделения «зарубежное регионоведение», решает такие важные задачи, как ознакомление студентов с основными понятиями математического анализа и смежных дисциплин (линейная алгебра, аналитическая геометрия), необходимыми для решения теоретических и практических задач экономики; воспитание абстрактного мышление и умения строго излагать свои мысли. Кроме того, он способствует подготовке обучающихся к практическому применению полученных знаний.
В связи с вышесказанным основное внимание уделяется практическим занятиям и самостоятельной работе студентов, организации которых и должно способствовать данное методическое пособие.
В первую часть включены вспомогательные разделы, изучение которых позволит легче осваивать азы математического анализа. Каждый из параграфов содержит необходимые теоретические положения, разобранные «типовые» задачи, которые сопровождаются указаниями по организации самостоятельной проверки полученного результата, а также упражнения для самостоятельного решения, позволяющие закрепить полученные навыки. При возникновении затруднений рекомендуется использовать следующую литературу:
1. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов. – СПб.: Лань, 2010
2. Выгодский М.Я. Справочник по высшей математике. – М.: ACT: Астрель, 2006.
3. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. – М.: АСТ: Астрель 2007.
4. Справочник по математике для экономистов /Под ред. В.И.Ермакова. – М.: Инфра-М, 2009.
ПРЕОБРАЗОВАНИЯ МАТРИЦ
1.1. Предварительные сведения. Матрицей называется прямоугольная таблица чисел, состоящая из m строк и n столбцов, которую записывают в следующем виде:
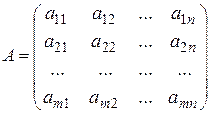 .
.
Для обозначения матрицы используют прописные латинские буквы, причем в скобках указывается размер – количество строк и столбцов. Так, запись B(2x3) означает, что речь идет о матрице, состоящей из двух строк и трех столбцов, например 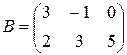 . Далее, bij - обозначение элемента, стоящего на пересечении i-й строки и j-го столбца данной матрицы (в примере b23=5). Через Ai обозначают i -ю строку матрицы A , через Aj – j -й столбец.
. Далее, bij - обозначение элемента, стоящего на пересечении i-й строки и j-го столбца данной матрицы (в примере b23=5). Через Ai обозначают i -ю строку матрицы A , через Aj – j -й столбец.
Матрицы A , B называются равными (A = B), если они имеют одинаковый размер, и их элементы, стоящие на одинаковых позициях, совпадают.
Матрица, у которой число строк совпадает с числом столбцов, называется квадратной. Элементы квадратной матрицы A ( nxn) a11 , a22 ,…, ann образуют главную диагональ. Квадратная матрица, у которой отличные от нуля элементы могут стоять только на главной диагонали, называется диагональной. Диагональная матрица, у которой все элементы (главной диагонали!) равны 1, называется единичной. Наконец, квадратная матрица, у которой ниже (выше) главной диагонали находятся только нули, называется верхней (нижней) треугольной матрицей. Например, среди квадратных матриц размера 3 x 3
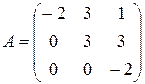 ,
, 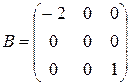 ,
, 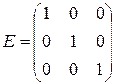 ,
, 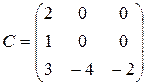
матрица A является верхней треугольной, B – диагональной, C – нижней треугольной, E – единичной.
1.2. Арифметические действия с матрицами. Чтобы умножить матрицу A (mxn) на отличное от нуля вещественное число k, необходимо каждый элемент матрицы умножить на это число:
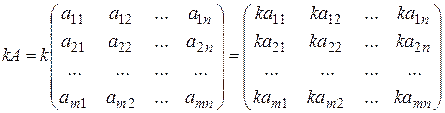 .
.
Чтобы найти сумму матриц A (mxn), B(mxn) (одного и того же размера!), необходимо сложить элементы с одинаковыми индексами (стоящие на одинаковых местах):
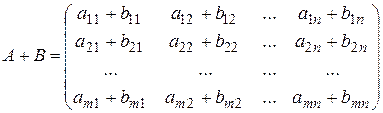 .
.
При этом речь идет об алгебраической разности, т.е. при вычислении A - B находим разность элементов, стоящих на одинаковых местах.
Пример 1.1. Найти 2 A - B, если 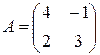 ,
, 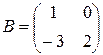 .
.
Решение. Сначала умножаем матрицу A на число "2", затем находим разность:
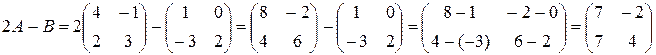
Произведение AB можно определить только для матриц размера A(mxn), B(nxp), при этом AB=C, матрица C имеет размер C(mxp) и ее элемент cij находится как скалярное произведение i-й строки матрицы A на j-й столбец матрицы B, т.е. 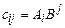 ( i =1,2,..., m ; j =1,2,..., p ). Фактически каждую строку матрицы A необходимо скалярно умножить на каждый столбец матрицы B
( i =1,2,..., m ; j =1,2,..., p ). Фактически каждую строку матрицы A необходимо скалярно умножить на каждый столбец матрицы B
Пример 1.2. Найти AB и BA для 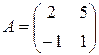 и
и 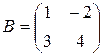 .
.
Решение. Размеры матриц 2х2, поэтому оба произведения определены:
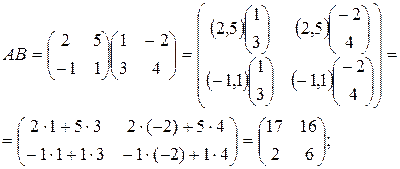
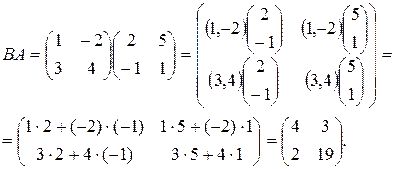
Как видно, 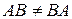 , т.е. эта операция не коммутативна.
, т.е. эта операция не коммутативна.
Матрицей, транспонированной к матрице A (mxn), называется матрица AT (nxm), строки которой являются соответствующими столбцами исходной матрицы. Например, если 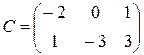 , то
, то 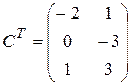 .
.
Пример 1.3. Вычислить AB +2 CT, если 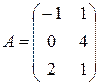 ,
, 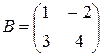 ,
, 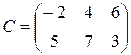 .
.
Решение. Учитывая все правила действий с матрицами, получаем:
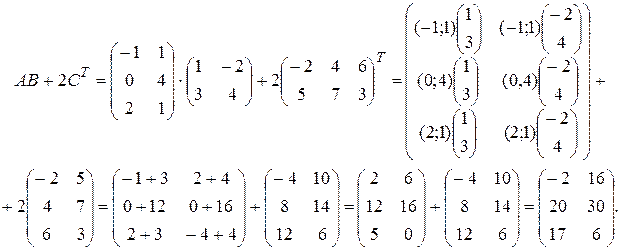
1.3. Элементарные преобразования матриц.К таким преобразованиям матриц относятся следующие действия:
1) перемена местами двух строк матрицы (краткая запись: 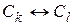 );
);
2) вычеркивание нулевой строки матрицы (строки, в которой все элементы равны нулю);
3) умножение всех элементов одной строки матрицы на одно и то же число, отличное от нуля (коротко: 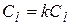 );
);
4) прибавление к элементам одной строки матрицы соответствующих элементов другой ее строки, умноженных на одно и то же отличное от нуля число (коротко: 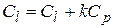 ).
).
Так как вычеркивание нулевой строки приводит к изменению размера матрицы, говорить о равенстве матриц при подобных преобразованиях нельзя.
Матрицы A, B называются эквивалентными, если одна получена из другой путем элементарных преобразований.
Матрица A (mxn) называется ступенчатой, если в каждой ее строке есть элемент, в столбце которого все элементы ниже являются нулями, а в последней строке есть хотя бы один ненулевой элемент. Упомянутые в определении ненулевые элементы называют ведущими.
Ступенчатыми являются, например, треугольные матрицы, матрицы  ,
, 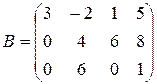 и т.д.
и т.д.
Любую ненулевую матрицу можно путем элементарных преобразований свести к эквивалентной ей ступенчатой. Алгоритм доказательства этого утверждения совпадает с алгоритмом практического преобразования матрицы.
Пример 1.4. Привести к ступенчатому виду матрицы 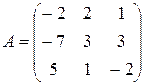 ,
, 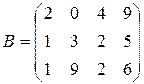 .
.
Решение. При преобразованиях матрицы A ведущим элементом в первой строке будет a 13, во второй a21 . Имеем:
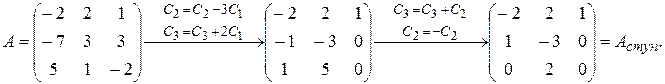
Итак, 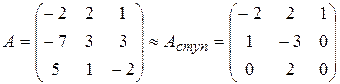 . Ведущим элементом в третьей строке является a32 .
. Ведущим элементом в третьей строке является a32 .
Проведем преобразования для матрицы B и покажем, что
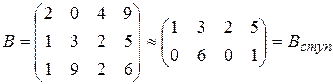
Действительно,
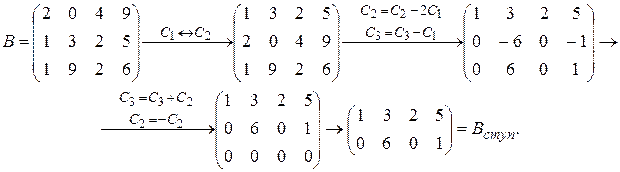 .
.
В первой строке ведущим является элемент b 11, во второй в качестве ведущего может выступить либо b22, либо b24.
Рангом матрицы A (mxn) в дальнейшем будем называть число строк эквивалентной ей ступенчатой матрицы. Стандартное обозначение ранга матрицы A (mxn): r ( A ). Так, в примере 1.4 r ( A )=3, r ( B )=2.
Замечание. Ранг матрицы не зависит ни от выбора ведущих элементов, ни от проводимых преобразований. Поэтому полученный результат всегда можно проверить, попытавшись привести матрицу к ступенчатой другим способом. Например, после перестановки первой и второй строки в матрице B можно в качестве ведущего сначала рассмотреть элемент b 12:
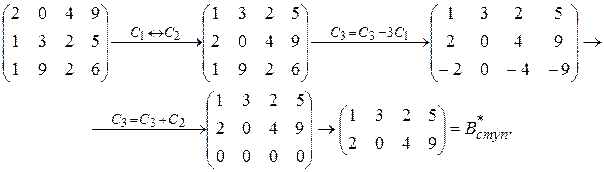 Получили другую матрицу, эквивалентную B. Но она тоже является ступенчатой, причем состоит из двух строк, поэтому и в данном случае r ( B )=2.
Получили другую матрицу, эквивалентную B. Но она тоже является ступенчатой, причем состоит из двух строк, поэтому и в данном случае r ( B )=2.
Задания для самостоятельного решения.
Упражнение 1.1. Выполнить арифметические действия с матрицами:
1) а) 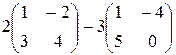 ; б)
; б) 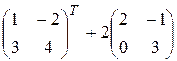
2) 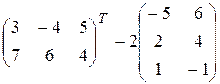 ; 3)
; 3) 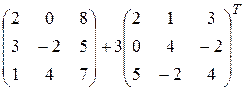 ;
;
4) 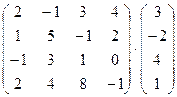 ; 5)
; 5) 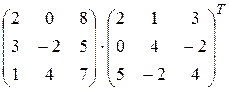 ;
;
6) 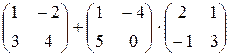 ; 7)
; 7) 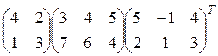 ;
;
8) 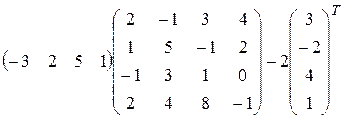 ;
;
9) 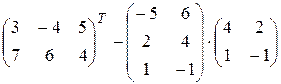
10) 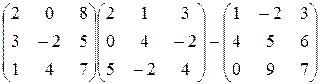 ;
;
11) 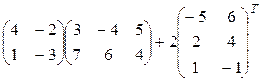 .
.
Упражнение 1.2. Найти значение заданного многочлена P(X) от заданной матрицы X (всюдув задании E – единичная матрица нужного размера):
1) 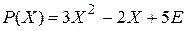 ,
,  ; 2)
; 2) 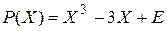 ,
, 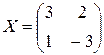 ;
;
Упражнение 1.3. Решить матричные уравнения (O - нулевая матрица соответствующего размера):
1) 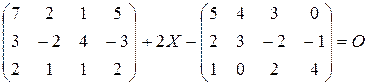 ;
;
2) 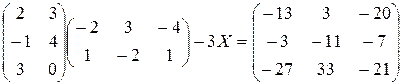 .
.
Упражнение 1.4. Проверить равенства AB = BA , ( AB ) C = A ( BC ) для матриц:
1) 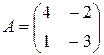 ,
, 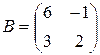 ,
, 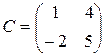 ;
;
2) 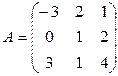 ,
, 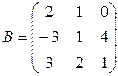 ,
, 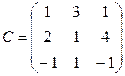 ;
;
3) 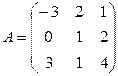 ,
, 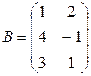 ,
, 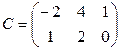 ;
;
Упражнение 1.5. Свести матрицу A к эквивалентной ей ступенчатой, определить ранг матрицы A:
1) 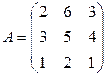 2)
2) 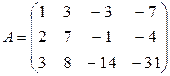 3)
3) 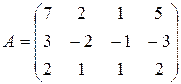
4) 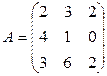 5)
5) 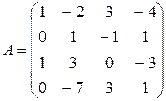 6)
6) 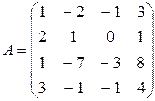
|
из
5.00
|
Обсуждение в статье: Задания для самостоятельного решения. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

