 |
Главная |
Задания для самостоятельного решения.
|
из
5.00
|
Упражнение 3.1. Доказать, что  :
:
1)  ,
,  ; 2)
; 2)  ,
,  ;
;
3)  ,
,  .
.
Упражнение 3.2. Проверить, имеет ли матрица обратную:
 ; ;
| 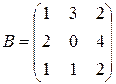 ; ;
|  ; ;
|  . .
|
Упражнение 3.3. Найти матрицы, обратные к данным, методом Гаусса и методом алгебраических дополнений.
1)  ; 2)
; 2)  ; 3)
; 3) 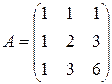 ;
;
4)  ; 5)
; 5)  ; 6)
; 6)  ;
;
Упражнение 3.4. Найти  удобным методом, сделать проверку.
удобным методом, сделать проверку.
1)  ; 2)
; 2)  ; 3)
; 3)  .
.
Упражнение 3.5. Решить матричные уравнения.
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  .
.
§ 4. ОБЩАЯ ТЕОРИЯ СИСТЕМ
ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ.
4.1. Основные обозначения.В п.2.2 рассматривались «квадратные» системы линейных алгебраических уравнений (далее будет использоваться сокращение СЛАУ). Теперь предметом изучения становятся СЛАУ произвольной размерности, состоящие из m уравнений с n неизвестными:
 . (10)
. (10)
Матрица  , составленная из коэффициентов системы (10), называется матрицей системы, векторы
, составленная из коэффициентов системы (10), называется матрицей системы, векторы  и
и  - вектором неизвестных и столбцом (вектором) свободных членов (соответственно). Матрицу вида
- вектором неизвестных и столбцом (вектором) свободных членов (соответственно). Матрицу вида 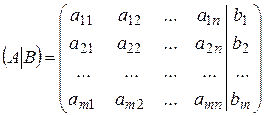 называют расширенной матрицей системы (10). Любой набор чисел
называют расширенной матрицей системы (10). Любой набор чисел  является решением системы (10), если эти числа удовлетворяют всем уравнениям системы (т.е. превращают их в тождества). В матричной форме записи система (10) имеет вид
является решением системы (10), если эти числа удовлетворяют всем уравнениям системы (т.е. превращают их в тождества). В матричной форме записи система (10) имеет вид  , так как при каждом i =1,2,…, m i -е уравнение представляет собой произведение i -й строки матрицы системы на вектор X
, так как при каждом i =1,2,…, m i -е уравнение представляет собой произведение i -й строки матрицы системы на вектор X
Пример 4.1. Записать СЛАУ  в виде (10), если
в виде (10), если  ,
,  .
.
Решение. Введем в рассмотрение вектор X и с каждым столбцом мысленно сопоставим неизвестное: с первым столбцом -  , со вторым -
, со вторым -  , с третьим -
, с третьим -  , с четвертым -
, с четвертым -  . Первое уравнение в (10), как отмечено выше, представляет собой скалярное произведение первой строки матрицы A на вектор X. Аналогично получаем второе и третье уравнение (используя, соответственно, вторую и третью строки). Заметим, что если коэффициент равен нулю, то соответствующее слагаемое в системе отсутствует. Окончательно нужная система линейных алгебраических уравнений имеет вид
. Первое уравнение в (10), как отмечено выше, представляет собой скалярное произведение первой строки матрицы A на вектор X. Аналогично получаем второе и третье уравнение (используя, соответственно, вторую и третью строки). Заметим, что если коэффициент равен нулю, то соответствующее слагаемое в системе отсутствует. Окончательно нужная система линейных алгебраических уравнений имеет вид  .
.
4.2. Классификация систем линейных алгебраических уравнений. Если СЛАУ (10) имеет хотя бы одно решение, она называется совместной (соответственно, система несовместная, если она вообще не имеет решений). Совместная система (10) называется определенной, если она имеет единственное решение, и неопределенной, если имеет более одного решения (в последнем случае у нее бесконечно много решений).
Матрицу системы (10) будем называть приведенной, если в каждой ее строке есть элемент, равный 1, а все остальные элементы этого столбца равны нулю. Соответствующая приведенной матрице система линейных алгебраических уравнений называется канонической, элементы, равные 1 (и соответствующие им неизвестные) называются ведущими (базисными), а оставшиеся неизвестные – свободными.
Теорема Кронекера-Капелли. СЛАУ (10) совместна тогда и только тогда, когда ранг матрицы системы совпадает с рангом ее расширенной матрицы, т.е  .
.
Для совместной системы число  назовем рангом системы.
назовем рангом системы.
Теорема о количестве решений. Пусть СЛАУ (10) совместна. Если ее ранг равен числу неизвестных (  ), то система является определенной; если ранг системы меньше числа неизвестных (
), то система является определенной; если ранг системы меньше числа неизвестных ( 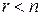 ), то исходная система – неопределенная.
), то исходная система – неопределенная.
Неопределенная система, как было отмечено, имеет бесконечное множество решений. Совокупность всех решений называется общим решением системы.
4.3. Алгоритм метода Гаусса.Цель рассуждений – путем элементарных преобразований свести исходную систему к равносильной, решение которой можно выписать непосредственно. Основными шагами метода Гаусса являются следующие.
I. Прямой ход. Выписать расширенную матрицу системы, путем элементарных преобразований свести ее к эквивалентной ступенчатой и определить ранги матрицы и расширенной матрицы системы. Если они различны, то исходная система в силу теоремы 4.1 несовместна, т.е. не имеет решений. Если  , то переходим к следующему этапу.
, то переходим к следующему этапу.
II. Сравнить ранг системы и число неизвестных, сделать вывод о количестве решений, учитывая теорему 4.2.
III. Обратный ход. Ступенчатую матрицу преобразовать к эквивалентной ей приведенной. Определить, какие неизвестные являются ведущими, какие – свободными.
IV. Выписать по полученной матрице систему, записать ответ (выразив, в случае необходимости, ведущие элементы через свободные).
Пример 4.2. Решить СЛАУ 
Решение. Приведем расширенную матрицу к ступенчатому виду:

Очевидно, что 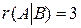 , а
, а  (матрица A расположена слева от вертикальной черты и у нее третья строка состоит только из нулей!). Таким образом, ранги различны, а система несовместна.
(матрица A расположена слева от вертикальной черты и у нее третья строка состоит только из нулей!). Таким образом, ранги различны, а система несовместна.
Пример 4.3. Решить СЛАУ  .
.
Решение. Преобразуем расширенную матрицу системы:

Последняя матрица – ступенчатая. Ведущими неизвестными для нее являются  в первой строке,
в первой строке,  во второй и
во второй и  в третьей. Очевидно, что система совместна и ее ранг равен 3:
в третьей. Очевидно, что система совместна и ее ранг равен 3:  . Поскольку число неизвестных также равно 3, исходная система является определенной.
. Поскольку число неизвестных также равно 3, исходная система является определенной.
Переходим к проведению преобразований по обратному методу Гаусса (теперь необходимо получать нули НАД ведущими элементами).
 Теперь составляем по последней матрице систему:
Теперь составляем по последней матрице систему: 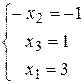 и выписываем значения неизвестных в порядке их номеров: X =(3;1;1). Это и есть ответ, записанный в виде вектор-строки (так удобнее).
и выписываем значения неизвестных в порядке их номеров: X =(3;1;1). Это и есть ответ, записанный в виде вектор-строки (так удобнее).
Заметим, что эта же система была решена в примере 2.4, ответы совпали. В дальнейшем для проверки результата можно пользоваться подстановкой найденных значений в уравнения системы.
Пример 4.4. Для СЛАУ  найти общее и два частных решения.
найти общее и два частных решения.
Решение. Приведем расширенную матрицу системы к ступенчатому виду:

Очевидно, что  , число неизвестных n =4 и в соответствии с теоремой 4.2 исходная система является неопределенной. Ведущие неизвестные:
, число неизвестных n =4 и в соответствии с теоремой 4.2 исходная система является неопределенной. Ведущие неизвестные:  в первой строке,
в первой строке,  во второй,
во второй,  в третьей. Свободное неизвестное -
в третьей. Свободное неизвестное -  . Обратным ходом преобразуем матрицу к приведенному виду:
. Обратным ходом преобразуем матрицу к приведенному виду:

Выписываем полученную систему, ведущие неизвестные выражаем через свободные:  . Общее решение записываем в порядке нумерации неизвестных:
. Общее решение записываем в порядке нумерации неизвестных:  ,
,  .
.
Частное решение можно получить, если придать  конкретное числовое значение. Например, при
конкретное числовое значение. Например, при  имеем
имеем  , а при
, а при 
 .
.
4.4. Метод обратной матрицы. Предположим, что в системе AX = B матрица A невырожденная, т.е. | A | ¹ 0. Тогда матрица A имеет обратную. Умножая равенство AX = B слева на  , получаем решение системы:
, получаем решение системы:  .
.
Пример 4.5. Решить с помощью обратной матрицы: 
Решение. Методом Гаусса найдем матрицу, обратную к матрице системы:

Итак,  . Теперь найдем решение исходной системы:
. Теперь найдем решение исходной системы: 
|
из
5.00
|
Обсуждение в статье: Задания для самостоятельного решения. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

