 |
Главная |
Числовые характеристики двумерного случайного вектора
|
из
5.00
|
54.1. Пусть случайные величины 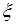 и
и  имеют совместную плотность вероятности
имеют совместную плотность вероятности  и
и  - функция двух переменных. Тогда
- функция двух переменных. Тогда  - случайная величина, полученная подстановкой случайных величин
- случайная величина, полученная подстановкой случайных величин 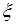 и
и  вместо аргументов
вместо аргументов  и
и 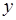 .
.
Математическим ожиданием случайной величины  называется число
называется число
 . (54.1)
. (54.1)
Если 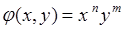 ,
, 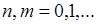 , тогда из (54.1) следует
, тогда из (54.1) следует
 ,
,  ,
,  . (54.2)
. (54.2)
Числа  называются начальными смешанными моментами порядка
называются начальными смешанными моментами порядка  случайных величин
случайных величин 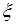 и
и  . Эти числа применяются в качестве статистических характеристик двумерного случайного вектора. Рассмотрим частные случаи (54.2). 1).
. Эти числа применяются в качестве статистических характеристик двумерного случайного вектора. Рассмотрим частные случаи (54.2). 1).  , тогда
, тогда  - начальный момент порядка
- начальный момент порядка  случайной величины
случайной величины  . При дополнительном условии
. При дополнительном условии  получаем
получаем 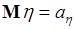 - математическое ожидание случайной величины
- математическое ожидание случайной величины  , при
, при  -
-  - среднее ее квадрата и т.д. Таким образом, при
- среднее ее квадрата и т.д. Таким образом, при  смешанные моменты (54.2) совпадают с начальными моментами случайной величины
смешанные моменты (54.2) совпадают с начальными моментами случайной величины  . 2). Если положить
. 2). Если положить  , тогда
, тогда 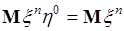 - смешанные моменты совпадают с начальными моментами случайной величины
- смешанные моменты совпадают с начальными моментами случайной величины 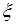 . В обоих случаях получаем индивидуальные характеристики одной из случайных величин. 3). Для получения групповой характеристики (54.2), отражающей свойства совокупности двух случайных величин, необходимо рассмотреть ненулевые
. В обоих случаях получаем индивидуальные характеристики одной из случайных величин. 3). Для получения групповой характеристики (54.2), отражающей свойства совокупности двух случайных величин, необходимо рассмотреть ненулевые  . Наиболее простой вариант:
. Наиболее простой вариант:  ,
,  . При этом из (54.2) следует
. При этом из (54.2) следует
 . (54.3)
. (54.3)
Число  называется корреляцией случайных величин
называется корреляцией случайных величин 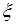 и
и  и представляет собой важнейшую характеристику совокупности двух случайных величин.
и представляет собой важнейшую характеристику совокупности двух случайных величин.
Если 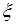 и
и  - независимы, то
- независимы, то  и (54.3) преобразуются следующим образом:
и (54.3) преобразуются следующим образом:

 , (54.4)
, (54.4)
где 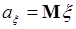 и
и  . При этом
. При этом  выражается через индивидуальные характеристики
выражается через индивидуальные характеристики  и
и  , т.е. каких-либо групповых эффектов в
, т.е. каких-либо групповых эффектов в  не проявляется, что является следствием независимости случайных величин
не проявляется, что является следствием независимости случайных величин 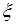 и
и  . Из цепочки преобразований (54.4) следует равенство
. Из цепочки преобразований (54.4) следует равенство  - математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.
- математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.
54.2. Аналогично (54.2) числа
 (54.5)
(54.5)
называются центральными смешанными моментами, порядка  . Наиболее важной групповой характеристикой двух случайных величин среди чисел (54.5) является ковариация
. Наиболее важной групповой характеристикой двух случайных величин среди чисел (54.5) является ковариация
 , (54.6)
, (54.6)
которая является центральным смешанным моментом порядка 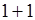 . Для ковариации используется также обозначение:
. Для ковариации используется также обозначение: 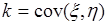 . Если
. Если  , то
, то  - совпадает с дисперсией случайной величины
- совпадает с дисперсией случайной величины 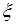 .
.
Если 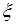 и
и  - независимы, то из (54.6) следует, что ковариация
- независимы, то из (54.6) следует, что ковариация
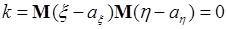 .
.
Обратное утверждение в общем случае неверно, т.е. из равенства  в общем не следует независимость случайных величин
в общем не следует независимость случайных величин 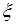 и
и  . В частности, обратное утверждение справедливо, если
. В частности, обратное утверждение справедливо, если 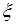 и
и  - гауссовы случайные величины. Более подробно этот вопрос обсуждается ниже.
- гауссовы случайные величины. Более подробно этот вопрос обсуждается ниже.
54.3. Найдем связь между корреляцией  и ковариацией
и ковариацией  случайных величин
случайных величин 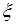 и
и  . Из определения ковариации (54.6) следует
. Из определения ковариации (54.6) следует

 .
.
Таким образом, ковариация  и корреляция
и корреляция  связаны соотношением
связаны соотношением
 . (54.7)
. (54.7)
|
из
5.00
|
Обсуждение в статье: Числовые характеристики двумерного случайного вектора |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

