 |
Главная |
Распределение вероятностей функции одной случайной величины
|
из
5.00
|
65.1. Пусть случайная величина  имеет плотность вероятности
имеет плотность вероятности  и функция одной переменной
и функция одной переменной 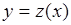 ,
,  , является взаимно однозначной, тогда плотность вероятности
, является взаимно однозначной, тогда плотность вероятности 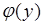 случайной величины
случайной величины  определяется соотношением:
определяется соотношением:
 , (65.1)
, (65.1)
где  - функция, обратная функции
- функция, обратная функции 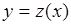 .
.
Вывод формулы (65.1) основан на соотношениях (64.4) и (64.6). Поскольку функция 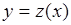 - взаимно однозначная, то эта функция или монотонно возрастающая
- взаимно однозначная, то эта функция или монотонно возрастающая  или монотонно убывающая
или монотонно убывающая 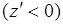 . Очевидны соотношения:
. Очевидны соотношения:
 , (65.2)
, (65.2)
 . (65.3)
. (65.3)
Пусть  ,
,  - функции распределения вероятностей случайных величин
- функции распределения вероятностей случайных величин  и
и  . Если
. Если  , тогда используя (65.2),
, тогда используя (65.2),
 . (65.4)
. (65.4)
Продифференцируем по  равенство (65.4), тогда
равенство (65.4), тогда
 . (65.5)
. (65.5)
Аналогично при 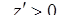 справедливо равенство (65.3), поэтому
справедливо равенство (65.3), поэтому
 (65.6)
(65.6)
Отсюда:
 . (65.7)
. (65.7)
Теперь из соотношений (65.5) и (65.7) следует (65.1).
Существенным условием при выводе формулы (65.1) является свойство взаимной однозначности функции 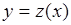 . Примерами таких функций являются: 1). Линейная функция
. Примерами таких функций являются: 1). Линейная функция 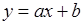 , где
, где 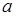 ,
,  - числа, при этом обратная функция имеет вид
- числа, при этом обратная функция имеет вид  ; 2). Экспонента -
; 2). Экспонента -  , откуда обратная функция
, откуда обратная функция  ,
,  , и другие. Однако условие взаимной однозначности функции
, и другие. Однако условие взаимной однозначности функции 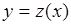 может нарушаться, например, для функции
может нарушаться, например, для функции 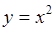 обратная функция
обратная функция  ,
, 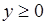 - двузначная. При этом рассматриваются две функции
- двузначная. При этом рассматриваются две функции 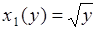 и
и  ,
, 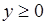 , которые называются первая и вторая ветви обратного преобразования
, которые называются первая и вторая ветви обратного преобразования  . Более сложный пример:
. Более сложный пример:  . Здесь обратная функция – многозначная.
. Здесь обратная функция – многозначная.
65.2. Рассмотрим модификацию формулы (65.1) на случай многозначного обратного преобразования  . Для этого на области определения функции
. Для этого на области определения функции 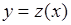 выделим неперекрывающиеся интервалы
выделим неперекрывающиеся интервалы  ,
,  - целое, на которых
- целое, на которых  , тогда на интервалах вида
, тогда на интервалах вида  выполняется условие
выполняется условие  . Функция
. Функция 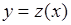 , для
, для  , монотонная возрастающая, а для
, монотонная возрастающая, а для  - монотонная убывающая. Поэтому для каждого из указанных интервалов существует однозначная обратная функция по отношению к функции
- монотонная убывающая. Поэтому для каждого из указанных интервалов существует однозначная обратная функция по отношению к функции  . Пусть функция
. Пусть функция 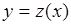 для
для  имеет обратную функцию вида
имеет обратную функцию вида  ,
,  , очевидно
, очевидно  - монотонная возрастающая, поскольку обратная ей
- монотонная возрастающая, поскольку обратная ей  - монотонная возрастающая. Аналогично обозначим через
- монотонная возрастающая. Аналогично обозначим через  - функцию со значениями
- функцию со значениями 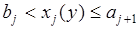 , обратную к
, обратную к  на интервале
на интервале  . Очевидно
. Очевидно  - монотонная убывающая. Функция
- монотонная убывающая. Функция  называется
называется  -я ветвь обратного преобразования функции
-я ветвь обратного преобразования функции 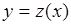 . Теперь по формуле сложения вероятностей для несовместных событий:
. Теперь по формуле сложения вероятностей для несовместных событий:
 (65.8)
(65.8)
где суммирование ведется по всем ветвям обратного преобразования.
На рис. 65.1. представлен простой пример функции  , у которой ветви обратного преобразования:
, у которой ветви обратного преобразования:  со значениями
со значениями  , и
, и  - со значениями
- со значениями 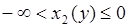 . На интервале
. На интервале  функция
функция  - монотонно возрастающая, а на интервале
- монотонно возрастающая, а на интервале 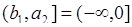 функция
функция  - монотонная убывающая. Равенство (65.8) в этом случае принимает вид:
- монотонная убывающая. Равенство (65.8) в этом случае принимает вид:
 .
.

Рис. 65.1. Пример преобразования случайной величины.
Представим вероятности в (65.8) через плотности вероятностей, тогда:
 . (65.9)
. (65.9)
Дифференцируя по  обе части (65.9), получим
обе части (65.9), получим
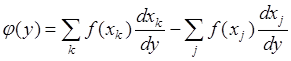 (65.10)
(65.10)
или
 , (65.11)
, (65.11)
где суммирование по  ведется по всем ветвям обратного преобразования.
ведется по всем ветвям обратного преобразования.
65.3. Рассмотрим примеры вычисления плотности вероятности случайной величины  по формуле (65.11). Пусть
по формуле (65.11). Пусть  - линейное преобразование случайной величины
- линейное преобразование случайной величины  . Функция
. Функция 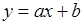 - взаимно однозначная, поэтому обратное преобразование имеет одну ветвь и сумма в (65.11) содержит одно слагаемое. Поскольку
- взаимно однозначная, поэтому обратное преобразование имеет одну ветвь и сумма в (65.11) содержит одно слагаемое. Поскольку  , то (65.11) принимает вид:
, то (65.11) принимает вид:
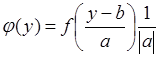 . (65.12)
. (65.12)
Рассмотрим квадратичное преобразование 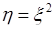 . Обратное преобразование имеет две ветви
. Обратное преобразование имеет две ветви  и
и 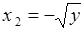 . Поэтому сумма (65.11) состоит из двух слагаемых. Вычисляя,
. Поэтому сумма (65.11) состоит из двух слагаемых. Вычисляя,  для
для  , получаем:
, получаем:
 (65.13)
(65.13)
Пусть  и случайная величина
и случайная величина  имеет равномерное распределение вероятностей на интервале
имеет равномерное распределение вероятностей на интервале  , с плотностью
, с плотностью  , если
, если 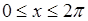 , и
, и 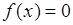 при
при 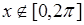 . Обратное преобразование имеет две ветви:
. Обратное преобразование имеет две ветви: 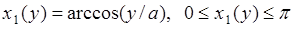 , а также
, а также 
 . Вычисление производных
. Вычисление производных  и подстановка в (65.11) приводит к результату:
и подстановка в (65.11) приводит к результату:
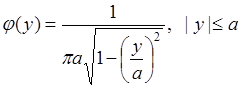 . (65.14)
. (65.14)
На рис. 65.2. представлен график плотности 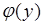 косинус-преобразования
косинус-преобразования
равномерно распределенной случайной величины. Таким образом, исходная

Рис. 65.2. Плотность вероятности косинус-преобразования.
исходная величина  и преобразованная величина
и преобразованная величина 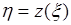 могут иметь совершенно непохожие плотности вероятности.
могут иметь совершенно непохожие плотности вероятности.
|
из
5.00
|
Обсуждение в статье: Распределение вероятностей функции одной случайной величины |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

