Преобразование нескольких случайных величин

66.1. Соотношение (65.11), определяющее плотность вероятности 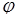 преобразованной величины  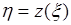через плотность  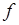исходной случайной величины 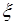, можно обобщить на случай преобразования  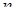случайных величин. Пусть случайные величины  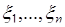имеют совместную плотность 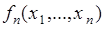, и заданы  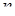функций 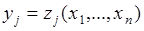,  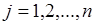переменных 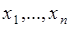. Необходимо найти совместную плотность вероятности  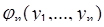случайных величин:

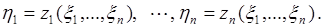                        (66.1)

Эта задача отличается от общей постановки, п. 6.4., условием 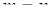 - число исходных случайных величин равно числу преобразованных величин. Преобразование, обратное (66.1), находится как решение системы уравнений 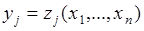, , 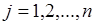относительно переменных 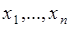. При этом каждое  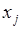зависит от 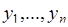. Совокупность таких функций 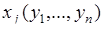, , 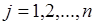образует обратное преобразование. В общем случае обратное преобразование неоднозначно. Пусть 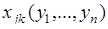, , 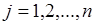- - я ветвь обратного преобразования 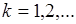, тогда справедливо соотношение:

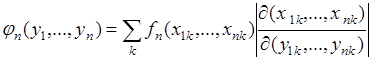 ,                      (66.2)

где сумма берется по всем ветвям обратного преобразования,

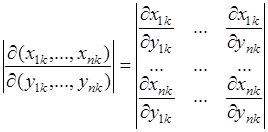                          (66.3)

- якобиан преобразования от случайных величин 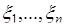 к случайным величинам .

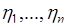Если из каждой совокупности 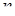 случайных величин получается  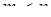случайных величин 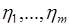, то формулой (66.2) можно воспользоваться, дополнив систему  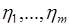до 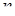 случайных величин, например, такими величинами 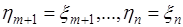. Если же 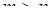, то  случайных величин из совокупности 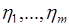 функционально связаны с остальными  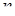величинами, поэтому 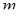- мерная плотность  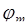будет содержать  дельта-функций.

Соотношения (64.4), (64.6) и (66.2) определяют два метода решения задачи вычисления плотности 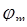 совокупности случайных величин 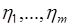, полученных функциональным преобразованием исходных случайных величин  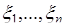с совместной плотностью вероятности 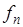. Основная трудность в применении первого метода состоит в вычислении 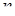-мерного интеграла по сложной области 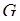. Во втором методе основная трудность – это нахождение всех ветвей обратного преобразования.

66.2. Рассмотрим простой пример вычисления плотности вероятности суммы двух случайных величин 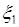 и 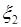 с плотностью  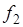по формуле (66.2). Очевидно, в качестве первой преобразованной величины следует выбрать сумму: 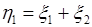, а в качестве второй  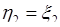(хотя можно взять и 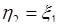). Таким образом, функциональное преобразование от 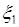,  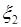к 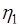,  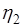задается системой уравнений:

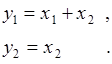                    (66.4)

Обратное преобразование – это решение системы уравнений относительно , :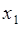

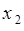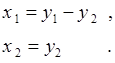          (66.5)

Обратное преобразование однозначно, поэтому в (66.2) сумма состоит из одного слагаемого. Найдем якобиан преобразования:

 .                                           

Теперь (66.2) для 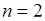 принимает вид:

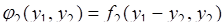 .              (66.6)

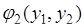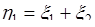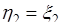Функция  - это совместная плотность вероятности случайных величин  и . Отсюда плотность вероятности  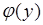суммы 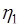 находится из условия согласованности:

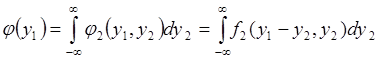.            (66.7)

Рассмотрим первый метод решения этой же задачи. Из (64.4) следует:

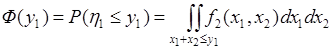.                  66.8)

Задача сводится к преобразованию интеграла по области 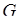, определяемой условием 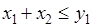. Этот интеграл можно представить в виде:

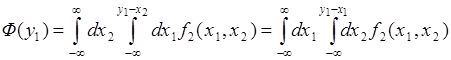(66.9)

Отсюда плотность вероятности:

Отсюда плотность вероятности:

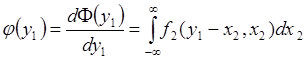 ,                (66.10)

что совпадает с формулой (66.7).