 |
Главная |
Выравнивание статистического закона распределения случайной величины Т
|
из
5.00
|
На практике число опытов n ограничено, и статистический закон распределения является каким-то приближением к теоретическому (истинному) закону распределения случайной величины Т. Стремятся подобрать такую теоретическую кривую, которая бы отражала существенные черты статистического закона распределения и не отражала бы случайностей из-за малого количества данных. Вид закона распределения подбирают из существа задачи, либо по внешнему виду статистического закона распределения.
Будем аппроксимировать статистический закон распределения случайной величины Т экспоненциальным законом распределения f(t).
Для экспоненциального закона распределения имеем
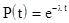 ;
;
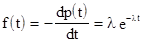 .
.
Нужно определить параметры выбранного закона распределения. Выбранный экспоненциальный закон распределения зависит от одного параметра 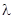 . Оценку параметра
. Оценку параметра 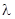 обозначим через
обозначим через 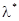 . Оценку
. Оценку 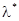 мы определяем из результатов опытов.
мы определяем из результатов опытов.
Используем для определения 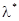 метод моментов; приравниваем теоретические и статистические моменты данного закона распределения. Имеем
метод моментов; приравниваем теоретические и статистические моменты данного закона распределения. Имеем
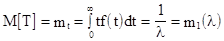 .
.
Здесь 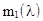 - первый теоретический момент. По результатам опытов определяем статистический первый момент
- первый теоретический момент. По результатам опытов определяем статистический первый момент 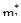 . Имеем
. Имеем
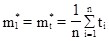 ;
;
где 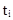 -время безотказной работы i - го изделия; n - число опытов или число изделий, поставленных на испытания. Приравниваем эти моменты
-время безотказной работы i - го изделия; n - число опытов или число изделий, поставленных на испытания. Приравниваем эти моменты
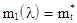
или 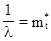
откуда 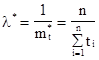
Пример 2: из результатов опытов определим 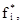 i =1, 2, …., k.
i =1, 2, …., k.
 Будем аппроксимировать статистический закон распределения случайной величины Т нормальным законом распределения f(t) вида
Будем аппроксимировать статистический закон распределения случайной величины Т нормальным законом распределения f(t) вида
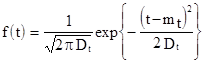
Нужно определить параметры выбранного закона распределения. Выбранный нормальный закон распределения зависит от двух параметров 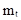 и
и 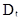 . Определим оценки
. Определим оценки 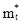 и
и 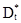 этих параметров из результатов опытов. Используем для определения
этих параметров из результатов опытов. Используем для определения 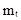 и
и 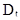 метод моментов. Теоретические моменты закона распределения случайной величины Т:
метод моментов. Теоретические моменты закона распределения случайной величины Т:
начальные моменты порядка S определяются соотношением
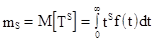 ; S = 1, 2,……;
; S = 1, 2,……;
центральные моменты порядка S определяются формулой
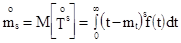 ; S = 1, 2, …….
; S = 1, 2, …….
Здесь 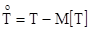 .
.
Определим 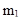 и
и 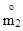 (
( 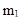 - начальный момент 1 - го порядка;
- начальный момент 1 - го порядка; 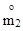 - центральный момент 2 - го порядка). Имеем:
- центральный момент 2 - го порядка). Имеем:
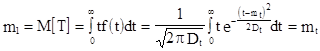 ;
;
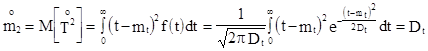 ;
;
Таким образом 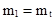 ;
;
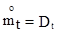 ;
;
По результатам опытов определяем статистические моменты 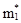 и
и 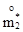 .
.
Имеем: 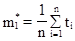 ;
;
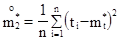 .
.
Приравниваем 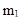 и
и 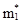 ,
, 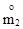 и
и 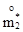 ; Имеем
; Имеем
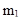 =
= 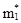 ,
, 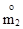 =
= 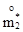 ;
;
или 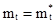 ,
, 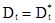 .
.
Следовательно 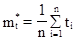 ;
;
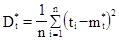 .
.
Для оценки степени расхождения статистического закона распределения с теоретическим законом распределения выбираем меру расхождения, по величине которой можно судить о том, вызвано ли расхождение случайными причинами, или разница между распределениями настолько велика, что выбранный теоретический закон распределения непригоден.
Обозначим меру расхождения через 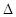 , которая может быть выбрана различными способами.
, которая может быть выбрана различными способами.
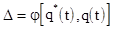 , где
, где 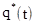 - статистическая функция распределения случайной Т ; q(t) - функция распределения случайной величины Т.
- статистическая функция распределения случайной Т ; q(t) - функция распределения случайной величины Т.
Например:
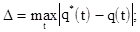
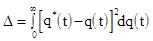 ;
;
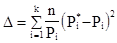 ;
;
где 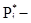 частота попадания случайной величины Т в интервал
частота попадания случайной величины Т в интервал 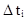 , i = 1, 2, …., K;
, i = 1, 2, …., K;
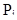 - вероятность попадания случайной величины Т в интервал
- вероятность попадания случайной величины Т в интервал 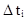 , i = 1, 2, …..K.
, i = 1, 2, …..K.
Чем меньше 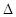 , тем лучше согласуется статистический закон распределения с теоретическим законом распределения.
, тем лучше согласуется статистический закон распределения с теоретическим законом распределения.
Выдвигаем гипотезу H о том, что выбранный нами закон распределения случайной величины Т не противоречит статистическому закону распределения. На основании имеющегося статистического материала следует проверить эту гипотезу H. Широко используются два критерия проверки гипотезы H: критерий Пирсона и критерий Колмогорова.
Критерий Пирсона
Разбиваем полученные в опытах значения Т на k интервалов:
k - число интервалов. Выдвигаем гипотезу H о том, что выбранная теоретическая плотность вероятности случайной величины Т есть функция f(t).
В качестве величины 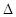 выбираем величину
выбираем величину 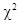 , определяемую по формуле
, определяемую по формуле
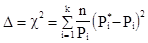 ;
;
где n - число опытов (число отказов);
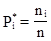 - частота попадания случайной величины Т в интервал
- частота попадания случайной величины Т в интервал 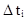 ;
;
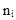 - количество значений случайной величины Т, попавших в интервал
- количество значений случайной величины Т, попавших в интервал 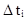 ;
;
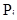 - вероятность попадания случайной величины Т в интервал
- вероятность попадания случайной величины Т в интервал 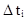 ;
;
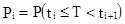 ;
; 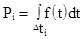 ; i = 1, 2, …., K;
; i = 1, 2, …., K; 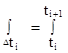 ;
;
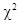 - это случайная величина.
- это случайная величина.
Можно доказать, что если верна гипотеза Н, то при 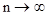 распределение величины
распределение величины 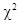 независимо от вида функции f(t) стремится к распределению
независимо от вида функции f(t) стремится к распределению 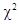 с числом степеней свободы
с числом степеней свободы
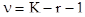 ; где K - число интервалов, r - число параметров функции f(t), оцениваемых по результатам опытов, по результатам статистической выборки объёма n.
; где K - число интервалов, r - число параметров функции f(t), оцениваемых по результатам опытов, по результатам статистической выборки объёма n.
Т.о. при 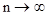
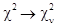
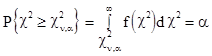 ;
;
Пусть 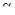 - такое число, что можно считать практически невозможным осуществление события с такой вероятностью
- такое число, что можно считать практически невозможным осуществление события с такой вероятностью 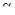 .
.
Если 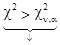 то
то 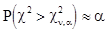 .
.
маловероятное событие для гипотезы Н.
Т.о, в этом случае гипотеза Н отклоняется, т.е выбранная теоретическая плотность вероятности не согласуется с результатами опытов.



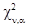
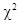
Область 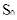 Область
Область 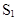
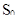 - область принятия гипотезы Н (выбранная теоретическая плотность вероятности согласуется с результатами опытов).
- область принятия гипотезы Н (выбранная теоретическая плотность вероятности согласуется с результатами опытов).
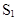 - область отклонения гипотезы Н.
- область отклонения гипотезы Н.
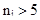 , n - порядка сотен.
, n - порядка сотен.
Критерий Колмогорова
Критерий Пирсона можно применять как для непрерывных, так и для дискретных случайных величин. Критерий Колмогорова применяется только для непрерывных случайных величин.
При использовании критерия Колмогорова сравниваются статистическая функция распределения 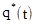 случайной величины Т и выбранная теоретическая функция распределения q(t). Предполагается, что значения параметров функции q(t) известны.
случайной величины Т и выбранная теоретическая функция распределения q(t). Предполагается, что значения параметров функции q(t) известны.
Если параметры теоретической функции распределения q(t) неизвестны, то вместо параметров могут использоваться оценки этих параметров, полученные по результатам опытов, т.е. по статистической выборке. В этом случае принимают 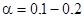 .
.
Определяем
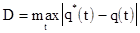 .
.
Определяем величину 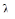
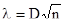 ;
;
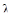 - случайная величина.
- случайная величина.
Выдвигаем гипотезу Н о том, что выбранная нами теоретическая функция распределения 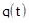 не противоречит статистической функции распределения
не противоречит статистической функции распределения 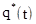 .
.
Колмогоров доказал следующую теорему.
Если верна гипотеза Н, то при 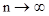 независимо от вида функции q(t) случайная величина
независимо от вида функции q(t) случайная величина 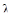 имеет функцию распределения вида
имеет функцию распределения вида
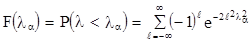 ;
;
тогда
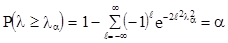 .
.
Методика проверки гипотезы Н по критерию Колмогорова:
1) определяем статистическую функцию распределения 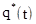 ;
;
2) определяем 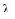 ;
;
3) для заданного  определяем
определяем 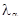 по таблице распределения Колмогорова.
по таблице распределения Колмогорова.
Если 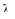
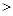
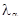 , то проверяемая гипотеза Н отклоняется, т.е. выбранная теоретическая функция распределения q(t) не согласуется (противоречит) статистической функции распределения
, то проверяемая гипотеза Н отклоняется, т.е. выбранная теоретическая функция распределения q(t) не согласуется (противоречит) статистической функции распределения 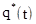 .
.
Если 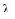 <
< 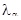 , то проверяемая гипотеза Н принимается, т.е. теоретическая функция распределения q(t) не противоречит функции распрделения
, то проверяемая гипотеза Н принимается, т.е. теоретическая функция распределения q(t) не противоречит функции распрделения 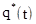 .
.








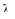
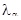
Область 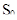 Область
Область 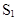
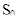 - область принятия гипотезы Н,
- область принятия гипотезы Н,
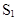 - область отклонения гипотезы Н.
- область отклонения гипотезы Н.
|
из
5.00
|
Обсуждение в статье: Выравнивание статистического закона распределения случайной величины Т |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

