Тема 1. Система линейных уравнений

 

    В общем случае система 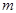 линейных уравнений с  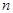неизвестными имеет вид

 

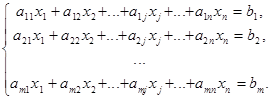 (1)

 

Через 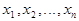 обозначены неизвестные, подлежащие определению, величины 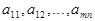, называемые коэффициентами системы, и величины 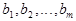, называемые свободными членами, считаются известными. Решением системы (1) называют такую совокупность  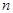чисел 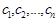, которая при подстановке в систему (1) на место неизвестных 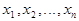обращает все уравнения системы в тождества. Система уравнений (1) либо не имеет решения, либо имеет единственное решение, либо имеет бесчисленное множество решений. Две системы линейных уравнений называются эквивалентными, если решение одной из них является решением другой и наоборот. Коэффициенты системы образуют матрицу, которую называют основной матрицей системы

 

.

 

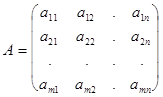Если 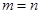, то матрица  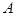является квадратной и ее определитель  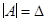называется определителем системы. Если определитель квадратной системы уравнений  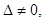то система имеет единственное решение, определяемое по формулам, называемых формулами Крамера:

 

 

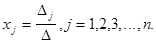
Здесь 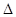- определитель системы, 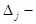определитель матрицы, получаемой из матрицы  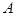заменой 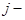го столбца столбцом ее свободных членов.

Пример 1. Решить систему линейных уравнений

 

 

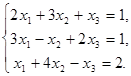
Решение. Найдем определитель системы

 

 =

 

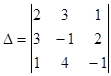
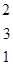
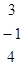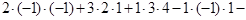
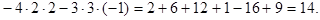
Далее вычислим определитель 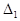, заменив первый столбец матрицы системы на столбец свободных членов

 

 

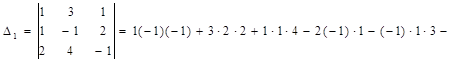
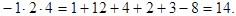
Аналогично находим определители :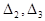

 

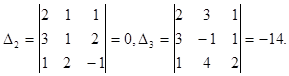
Отсюда по формулам Крамера находим решение системы

 

 

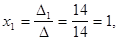
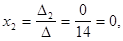
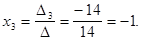
Общую систему линейных уравнений вида (1) можно решить методом Гаусса - методом последовательного исключения неизвестных. Исключение неизвестных методом Гаусса удобно выполнять, осуществляя преобразования не с самими уравнениями, а с матрицей их коэффициентов, к которой справа добавлен столбец свободных членов

 

 

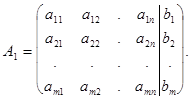
Полученную матрицу 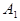 называют расширенной матрицей системы.

Элементарными преобразованиями строк матрицы называют:

Умножение всех элементов строки на число, не равное нулю.

Перестановка строк матрицы.

Прибавление к элементам строки соответствующих элементов другой строки, умноженных на общее произвольное число.

Метод Гаусса заключается в том, чтобы с помощью элементарных преобразований строк основную матрицу системы 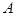 привести к ступенчатому (или треугольному) виду. Если вернуться к уравнениям, то это означает, что неизвестная  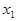содержится только в первом уравнении, неизвестная 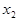- только в первом и втором уравнении и т. д. Таким образом, неизвестные системы частично исключаются из исходных уравнений системы, а полученная новая система уравнений является эквивалентной исходной системе. Рассмотрим решение методом Гаусса на примерах.

Пример 2. Решить систему уравнений

 

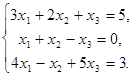 (2)

 

Решение. Расширенная матрица системы имеет вид

 

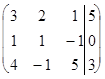 (3)

 

Поменяем местами первую и вторую строку в матрице (3), чтобы получить

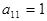 (в этом случае упрощаются последующие вычисления).

 

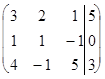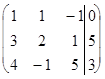~ (4)

 

Символ “~” обозначает эквивалентность матриц. Умножим первую строку полученной матрицы (4) на число (-3) и прибавим соответственно к элементам второй строки, далее первую строку матрицы (4) умножим на число (-5) и прибавим к элементам третьей строки этой матрицы. В результате получим матрицу, которой соответствует система уравнений, содержащая неизвестную 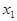 только в первом уравнении

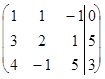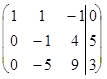 ~ . (5)

 

Так как в матрице (5) 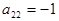, то, умножая вторую строку этой матрицы на число (-5) и прибавляя ее к третьей строке, получим основную матрицу треугольного вида. Для упрощения разделим элементы последней строки на число (-11):

 

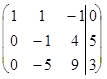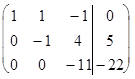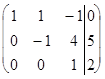~ ~  (6)

 

Расширенной матрице (6) соответствует следующая система уравнений, эквивалентная исходной системе (2)

 

 

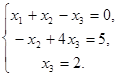
Отсюда из третьего уравнения получаем 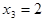. Подставляя найденное значение  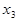во второе уравнение, определяем неизвестную :

 

 

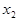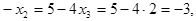
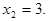
Наконец, после подстановки найденных значений 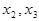 в первое уравнение, находим неизвестную 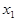:  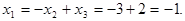Таким образом, решение системы единственное: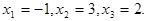

Пример 3. Решить систему уравнений

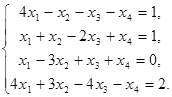 (7)

 

Решение. Запишем и преобразуем расширенную матрицу системы (7)

 

~ ~

 

~ ~ ~

 

~ ~ .

 

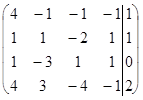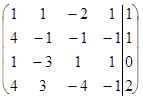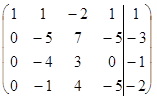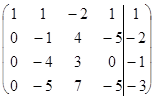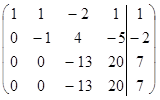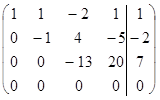Расширенная матрица, полученная на последнем шаге путем вычитания из элементов четвертой строки соответствующих элементов третьей строки, содержит нулевую строку и имеет ступенчатый вид. Отсюда следует, что исходной системе уравнений эквивалентна система из трех уравнений с 4 неизвестными

 

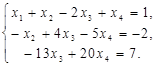
Неизвестную 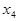 перенесем в правые части уравнений

 

 

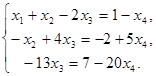
Отсюда определяем

 

 

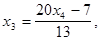
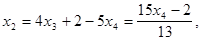
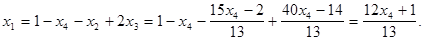
Задавая переменной 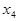 произвольное значение 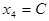, найдем бесконечное множество решений системы

 

 

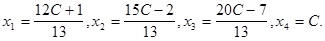
Если расширенная матрица системы приведена к ступенчатому виду, когда в нулевой строке основной матрицы свободный член отличен от нуля, то система не имеет решения. Например, последняя строка имеет вид 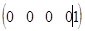. Тогда соответствующее уравнение системы привелось к неверному равенству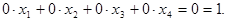

Пример 4. Предприятие выпускает три вида товаров, при производстве которых используется три типа ресурсов: рабочая сила, сырье, оборудование. Нормы расхода каждого из них (в условных единицах) на производство единицы каждого товара и объем ресурсов на 1 день заданы таблицей 1.

Таблица 1

Вид ресурсов	Норма расхода ресурсов на производство ед. товара			Объем ресурсов на 1 день
	1 вид	2 вид	3 вид
Рабочая сила	1	1	2	800
Сырье	3	2	4	1700
Оборудование	2	1	3	1100

 

Найти ежедневный объем выпуска каждого товара.

Решение. Пусть 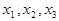 - ежедневный выпуск соответственно товаров 1,2 и 3-го вида. Тогда в соответствии с нормами расхода ресурсов каждого типа имеем систему линейных уравнений, содержащих неизвестные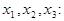

 

 

Решим ее методом Гаусса.

 

~ ~

 

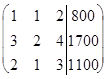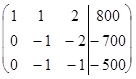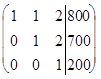
Отсюда находим 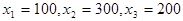, т.е. предприятие ежедневно выпускает 100 ед. товаров 1-го вида, 300 ед. товаров 2-го вида и 200 ед. товаров 3-го вида.

Задача для контрольной работы

Кондитерская фабрика специализируется на выпуске изделий трех видов. При этом используется сырье трех типов 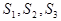. Нормы расхода каждого из них на одно изделие и общий объем расхода сырья на 1 день заданы таблицей 2. Найти ежедневный объем выпуска каждого вида изделия, построив систему линейных уравнений и решая ее методом Гаусса и по формулам Крамера.

 

Таблица 2

Номер варианта	Вид сырья	Норма расхода сырья на 1 изделие			Объем расхода сырья
		Изделие 1	Изделие 2	Изделие 3
1		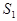3	2	4	2000
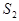
		1	3	2	1100
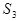
		2	5	1	1200
2		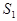4	1	3	1800
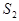
		1	2	5	2500
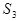
		2	1	2	1200
3		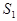2	3	4	1400
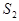
		3	1	3	1000
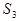
		1	2	3	1000
4		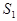1	5	2	1700
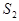
		2	3	1	1100
		3	1	4	1700
5		2	2	4	2200
		1	3	1	1300
		3	1	2	1600
6		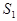1	3	3	1500
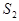
		3	1	1	900
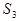
		2	2	4	1700
7		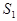4	2	1	1200
		3	3	2	1600
		1	2	1	900
8		1	2	2	1000
		3	1	2	1200
		4	3	4	2200
9		2	2	3	1000
		1	3	1	700
		3	1	2	700
10		1	3	4	2700
		2	1	3	1900
		3	2	1	1600