 |
Главная |
Задания на контрольную работу по теме
|
из
5.00
|
Задача 1 Исследовать сходимость числового ряда.
| Номер варианта | Исследуемые ряды | Номер варианта | Исследуемые ряды |
| 1 | а)  ; б) ; б)  . .
| 2 | а)  ; б) ; б)  . .
|
| 3 | а)  ; б) ; б)  . .
| 4 | а)  б) б)  . .
|
| 5 | а)  ; б) ; б)  . .
| 6 | а)  ; б) ; б)  . .
|
| 7 | а)  ; б) ; б)  . .
| 8 | а)  ; б) ; б) 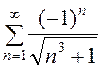 . .
|
| 9 | а)  ; б) ; б)  .
. .
.
| 10 | а)  ; б) ; б)  . .
|
Задача 2 Найти область сходимости степенного ряда.
| Номер варианта | Исследуемые ряды | Номер варианта | Исследуемые ряды |
| 1 | 
| 2 | 
|
| 3 | 
| 4 | 
|
| 5 | 
| 6 | 
|
| 7 | 
| 8 | 
|
| 9 | 
| 10 | 
|
Задача 3 Данную функцию представить в виде степенного
ряда по степеням (x – a), где а – данное число.
| № варианта | Функция и точка | № варианта | Функция и точка |
| 1 | 
| 2 | 
|
| 3 | 
| 4 | 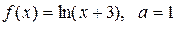
|
| 5 | 
| 6 | 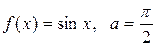
|
| 7 | 
| 8 | 
|
| 9 | 
| 10 | 
|
Задача 4 Построить эскиз графика, разложить в ряд Фурье следующие функции, периодические с периодом 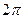 , определить сумму в точках разрыва. Построить график частичной суммы Фурье для n=4.
, определить сумму в точках разрыва. Построить график частичной суммы Фурье для n=4.
| № | Функция | № | Функция |
| 1 | 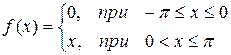
| 6 | 
|
| 2 | 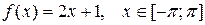
| 7 | 
|
| 3 | 
| 8 | 
|
| 4 | 
| 9 | 
|
| 5 | 
| 10 | 
|
Задача 5 Разложить в ряд Фурье в вещественной форме периодическую функцию  , с периодом Т=2l. Построить график частичной суммы при n=5.
, с периодом Т=2l. Построить график частичной суммы при n=5.
| № | Функция | T | № | Функция | T |
| 1 | f(x)=x+4 | 2 | 6 | f(x)=2x+1 | 3 |
| 2 | f(x)=-x+4 | 4 | 7 | f(x)=2x-1 | 5 |
| 3 | f(x)=2x+4 | 6 | 8 | f(x)=3x+4 | 7 |
| 4 | f(x)=x+1 | 2 | 9 | f(x)=3x-2 | 3 |
| 5 | f(x)=-x+2 | 4 | 10 | f(x)=-3x-1 | 1 |
Задача 6 Разложить в ряд Фурье в комплексной форме периодическую функцию с периодом  , определенную следующим образом:
, определенную следующим образом:  ,
,  . Построить амплитудно-частотный спектр.
. Построить амплитудно-частотный спектр.
| № | Функция | № | Функция |
| 1 | 
| 6 | 
|
| 2 | 
| 7 | 
|
| 3 | 
| 8 | 
|
| 4 | 
| 9 | 
|
| 5 | 
| 10 | 
|
Решение примерного варианта
Задача 1 Исследовать сходимость числового ряда.
а)  .
.
К данному знакоположительному ряду применим признак Даламбера:
 ; ряд расходится.
; ряд расходится.
Ответ: ряд расходится.
б)  .
.
Исследуем данный знакочередующийся ряд на абсолютную сходимость, рассмотрев ряд, составленный из модулей его членов:
 .
.
Полученный знакоположительный ряд сравним по второму признаку сравнения с гармоническим рядом  , про который известно, что он расходится:
, про который известно, что он расходится:
 .
.
Предел существует и не равен нулю; следовательно, согласно признаку, исследуемый ряд, как и гармонический, тоже расходится. Значит, исходный знакочередующийся ряд абсолютной сходимости не имеет.
Проверим теперь, обладает ли исходный знакочередующийся ряд условной сходимостью. Для этого используем признак Лейбница:
 ;
;
 , т.е. для любых
, т.е. для любых  выполняется условие
выполняется условие 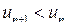 .
.
Оба условия признака Лейбница выполняются, т.е. по признаку Лейбница ряд сходится. Таким образом, исходный знакочередующийся ряд сходится условно.
Ответ: ряд сходится условно.
Задача 2 Найти область сходимости степенного ряда.
 .
.
Здесь центр сходимости  . Найдем радиус сходимости по формуле (16), полученной из признака Даламбера:
. Найдем радиус сходимости по формуле (16), полученной из признака Даламбера:
 .
.
Так как при  функции
функции  и
и  являются эквивалентными бесконечно малыми, то при
являются эквивалентными бесконечно малыми, то при  эквивалентны бесконечно малые
эквивалентны бесконечно малые  и
и  , а также
, а также  и
и  . Поэтому
. Поэтому
 .
.
По найденному радиусу сходимости получаем гарантированный интервал абсолютной сходимости:
 .
.
Исследуем сходимость ряда на границах этого интервала.
·  .
.
Этот знакочередующийся ряд не имеет абсолютной сходимости, т.к.
 , и ряд
, и ряд  расходится (второй, предельный признак сравнения). В то же время для него выполняются условия
расходится (второй, предельный признак сравнения). В то же время для него выполняются условия  и
и 
 , т.к.
, т.к.  - возрастающая функция. Следовательно, ряд сходится по признаку Лейбница, т.е. исходный степенной ряд в т.
- возрастающая функция. Следовательно, ряд сходится по признаку Лейбница, т.е. исходный степенной ряд в т.  сходится условно.
сходится условно. 
·  .
.
Этот знакоположительный числовой ряд также можно сравнить с расходящимся рядом  по второму признаку сравнения, из чего следует, что ряд
по второму признаку сравнения, из чего следует, что ряд 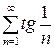 расходится.
расходится.
Ответ: область сходимости данного степенного ряда:  .
.
Задача 3 Данную функцию представить в виде степенного
ряда по степеням (x – a), где а – данное число:  .
.
Решение
Требуется разложить функцию по степеням двучлена  . Обозначим его новой переменной:
. Обозначим его новой переменной:  . Тогда
. Тогда 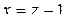 , и
, и  . Последнее выражение представим в виде
. Последнее выражение представим в виде  и введем еще одну переменную:
и введем еще одну переменную:  . После этого
. После этого  . Теперь для функции
. Теперь для функции  применим ее известное разложение в ряд Маклорена (см. справочную информацию):
применим ее известное разложение в ряд Маклорена (см. справочную информацию):
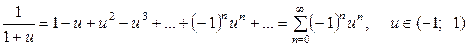 .
.
В последнем разложении возвратимся к переменной  и далее к исходной переменной
и далее к исходной переменной  :
:
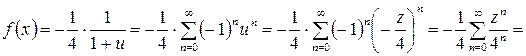
 .
.
Найдем теперь область сходимости. Для переменной 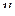 ее составляет интервал
ее составляет интервал  , т.е.
, т.е.  . Тогда
. Тогда  и
и  . Отсюда получаем, что
. Отсюда получаем, что  .
.
Ответ: 
 ,
,  .
.
Задача 4 Построить эскиз графика, разложить в ряд Фурье функцию  , имеющую период
, имеющую период  . Определить сумму в точках разрыва. По строить график частичной суммы ряда Фурье для n = 4.
. Определить сумму в точках разрыва. По строить график частичной суммы ряда Фурье для n = 4.
Решение Построим график функции

Эта функция f ( x ) имеет период  , одну точку разрыва первого рода x=0 на отрезке
, одну точку разрыва первого рода x=0 на отрезке  , отрезок
, отрезок  можно разбить на два отрезка так, что внутри каждого из них функция f ( x ) монотонна.
можно разбить на два отрезка так, что внутри каждого из них функция f ( x ) монотонна.
По формуле (2) найдем коэффициент  этого ряда.
этого ряда.
 .
.
Найдем  по формуле (3)
по формуле (3)

По формуле (4)  найдем аналогичным образом
найдем аналогичным образом

 .
.
Подставляя коэффициенты в формулу (1), получаем  или
или  .
.
Это равенство справедливо во всех точках, кроме точек разрыва. В каждой точке разрыва сумма ряда равна среднему арифметическому ее предельных значений изнутри отрезка, то есть в точке x=0.
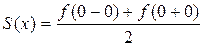 =
=  , а на концах отрезка в точках
, а на концах отрезка в точках  и
и 
 =
= 
 .
.
Ответ. 
Построим график S4(x)

Задача 5 Разложить в ряд Фурье в вещественной форме периодическую функцию  , с периодом Т=6. Построить график частичной суммы при n = 5.
, с периодом Т=6. Построить график частичной суммы при n = 5.
Решение
Построим эскиз графика функции 
Проверив выполнение условий Дирихле для функции, переходим к вычислению коэффициентов Фурье. Заданная функция общего вида с периодом Т=6, l=3, поэтому в разложении ее ряд Фурье имеет вид:  .
.

Подставляя коэффициенты в формулу ряда, получаем  или
или 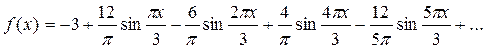 . Это равенство имеет место во всех точках, кроме точек -3 и 3. В каждой из этих точек сумма ряда равна среднему арифметическому ее предельных значений справа и слева, то есть
. Это равенство имеет место во всех точках, кроме точек -3 и 3. В каждой из этих точек сумма ряда равна среднему арифметическому ее предельных значений справа и слева, то есть  .
.
Построим график S5 (x)

Можно совместить оба графика на одном чертеже

Отметим близость этих графиков.
Задача 6 Разложить в ряд Фурье в комплексной форме периодическую функцию с периодом  , определенную следующим образом:
, определенную следующим образом:  . Построить амплитудно-частотный спектр.
. Построить амплитудно-частотный спектр.
Решение. Будем считать функцию периодической с периодом Т =2. Построим график.

Проверив выполнение условий Дирихле для функции  , переходим к вычислению коэффициентов Фурье по формуле
, переходим к вычислению коэффициентов Фурье по формуле  .
.
Интеграл, стоящий в правой части последнего равенства, определяется по частям:

 ;
; 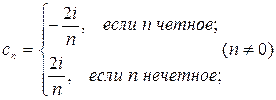
Если  , то полученные формулы не дают результата. Поэтому коэффициент
, то полученные формулы не дают результата. Поэтому коэффициент  надо вычислить иначе׃
надо вычислить иначе׃  , так как интеграл от нечетной функции по симметричному промежутку равен нулю. Окончательно получим
, так как интеграл от нечетной функции по симметричному промежутку равен нулю. Окончательно получим 
Это равенство имеет место лишь в точках непрерывности функции  . В точках разрыва
. В точках разрыва  , где k- любое нечетное число, сумма ряда равна нулю. Построим амплитудно-частотный спектр
, где k- любое нечетное число, сумма ряда равна нулю. Построим амплитудно-частотный спектр

Вопросы к экзамену
1. Основные понятия числовых рядов.
2. Необходимый признак сходимости рядов.
3. Достаточные признаки сходимости рядов.
4. Определение знакочередующихся и знакопеременных рядов.
5. Признаки сходимости знакочередующихся рядов.
6. Абсолютную и условную сходимость числового ряда.
7. Определение функционального ряда.
8. Сходимость функциональных рядов.
9. Определение степенного ряда.
10. Формулы радиуса и области сходимости степенного ряда.
11. Определение гармонического колебания.
12. Сформулируйте теорему Дирихле.
13. Определение ряда Фурье с периодом Т = 2  .
.
14. Определение ряда Фурье для четной функции.
15. Запишите ряд Фурье для нечетной функции .
16. Определение ряда Фурье с произвольным периодом Т = 2l.
17. Определение ряда Фурье с произвольным периодом четной функции.
18. Определение ряда Фурье с произвольным периодом нечетной функции.
19. Определение ряда Фурье для непериодической функции, заданной на некотором интервале (а, в).
20. Определение комплексной формы разложения функции в ряд Фурье.
21. Определение амплитудного спектра ряда Фурье в комплексной форме.
|
из
5.00
|
Обсуждение в статье: Задания на контрольную работу по теме |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

