 |
Главная |
Методические указания по темам
|
из
5.00
|
| № задачи | Тема | Литература |
| 1 | Определение числового ряда. Основные понятия: общий член, частичная сумма, сумма ряда, сходимость и расходимость. Свойства числовых рядов. Необходимый признак сходимости. Достаточные признаки сходимости знакоположительных рядов: признаки сравнения, признак Даламбера, радикальный признак Коши, интегральный признак Коши. Знакопеременные числовые ряды, их абсолютная и условная сходимости. Знакочередующиеся числовые ряды. Признак Лейбница сходимости знакочередующегося ряда | [1]: гл.XIII, §59; [2]: гл.XVI, §1,2. [1]: гл.XIII, §60; [2]: гл.XVI, §3-6. [1]: гл.XIII, §61; [2]: гл.XVI, §7,8. |
| 2 | Функциональный ряд: определения и основные понятия. Область сходимости функционального ряда. Определение степенного ряда. Теорема Абеля. Радиус сходимости. Способы определения радиуса сходимости степенного ряда. | [1]: гл.XIV, §62; [2]: гл.XVI, §9. [1]: гл.XIV, §63; [2]: гл.XVI, §13,14. |
| 3 | Дифференцирование и интегрирование степенных рядов.
Ряды Тейлора и Маклорена. Разложение в ряд Маклорена функции 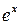 . Разложение в ряд Маклорена функций . Разложение в ряд Маклорена функций  и и  . Области сходимости этих рядов.
Разложение в ряд Маклорена биномиальной функции . Области сходимости этих рядов.
Разложение в ряд Маклорена биномиальной функции  ; область сходимости этого ряда. Разложение в ряд Маклорена функций ; область сходимости этого ряда. Разложение в ряд Маклорена функций 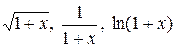 ; области сходимости этих рядов. ; области сходимости этих рядов.
| [1]: гл.XIV, §63; [2]: гл.XVI, §14. [1]: гл.XIV, §64; [2]: гл.XVI, §15-17. [1]: гл.XIV, §64; [2]: гл.XVI, §19,20. |
| 4 | Применение степенных рядов для приближенного вычисления функций. Оценка погрешности. | [1]: гл.XIV, §65; [2]: гл.XVI, §20,21. |
| 5 | Применение степенных рядов для приближенного вычисления определенных интегралов. Оценка погрешности. | [1]: гл.XIV, §65; [2]: гл.XVI, §21. |
| 6 | Тригонометрический функциональный ряд. Тригонометрический ряд для функции, заданной на отрезке  Теорема Дирихле о сходимости ряда Фурье для функции, заданной на отрезке Теорема Дирихле о сходимости ряда Фурье для функции, заданной на отрезке  Ряд Фурье для функции с периодом
Ряд Фурье для функции с периодом  . Ряд Фурье для функции с произвольным периодом. Ряды Фурье для четной и нечетной функции.
Разложение в ряд Фурье функции, заданной в интервале . Ряд Фурье для функции с произвольным периодом. Ряды Фурье для четной и нечетной функции.
Разложение в ряд Фурье функции, заданной в интервале 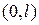 . .
| [1]: гл.XV, §66,67; [2]: гл.XVII, §1,2. [2]: гл.XV, §67; [1]: гл.XVII, §3-5. [2]: гл.XV, §67; [1]: гл.XVII, §6. |
| 7 | Гармонические колебания. Тригонометрический ряд. Ряд Фурье | [1], гл.VII, §29, 30; [2], гл.7, §1-4; [3], ч.1, гл.IX, №1337-1349, 1368-1379, 1392- [4], гл.6, № 2-12, 36-50, 102, 108, 114, 118 |
| 8 | Ряд Фурье для функций с произвольным периодом | [1], гл.VII, §31, 32; [2], гл.7, §5, 6.3; [3], ч.1, гл.IX, №1410-1414, 1429-1434, 1489-1490, 1493-1499; [4], гл.6, № 174, 177-180, 193, 195-201, 230-240 |
| 9 | Ряд Фурье для четных и нечетных функций | [1], гл.VIII, §35-40; [2], гл.8, §1, 4-9, 11; [3], ч.1, гл.X, №1552-1557, 1572-1578; [4], гл.6, № 262-273, 255-260, 366-369 |
| 10 | Ряд Фурье функции, заданной на отрезке [0, π] по синусам или по косинусам | [1], гл. VIII, §41, 41.1, 41.2; [2], гл.8, §10.1, 10.2; [3], ч.1, гл.X, №1596-1600; [4], гл.6, № 290-294,301, 302 |
Справочный материал по теме
Основные понятия о числовых рядах и определения
Числовой последовательностью называется упорядоченный набор нумерованных чисел  , представляющая собой функцию
, представляющая собой функцию
 ,
,  (1)
(1)
заданную на множестве натуральных чисел. Числа  называются соответственно первым, вторым и так далее членами последовательности. Число
называются соответственно первым, вторым и так далее членами последовательности. Число  , задаваемое формулой (1), называется общим членом последовательности.
, задаваемое формулой (1), называется общим членом последовательности.
В последовательностях и рядах широко используется функция натурального аргумента
 ,
,
представляющая собой произведение первых  натуральных чисел. Обозначение
натуральных чисел. Обозначение  читается как «эн факториал».
читается как «эн факториал».
Пусть u 1 , u 2 , u 3 ,…, un ,…, где un = f ( n ) , - бесконечная числовая последовательность. Тогда выражение

| (2) |
называется числовым рядом.
Числа  называются членами ряда. При этом
называются членами ряда. При этом
 , , 
|
называется общим членом ряда. Ряд считается заданным, если задана формула для  . Нумерация членов ряда, вообще говоря, может начинаться с любого целого числа.
. Нумерация членов ряда, вообще говоря, может начинаться с любого целого числа.
Сумму первых членов ряда по n-ный включительно обозначают Sn и называют n-ной частичной суммой ряда, т.е.

|
Сумму остальных слагаемых, начиная с  -го, называют n -ным остатком числового ряда и обозначают
-го, называют n -ным остатком числового ряда и обозначают  , т.е.
, т.е.
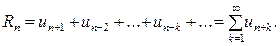
|
Согласно определению (2), остаток числового ряда можно рассматривать как самостоятельный числовой ряд.
Предел последовательности  частичных сумм при
частичных сумм при  , если он существует, называется суммой ряда и обозначается буквой S , т.е.
, если он существует, называется суммой ряда и обозначается буквой S , т.е.
 . .
|
Если  существует, т.е. если сумма S есть конечное число, то говорят, что ряд (2) сходится. В противном случае говорят, что ряд (2) расходится.
существует, т.е. если сумма S есть конечное число, то говорят, что ряд (2) сходится. В противном случае говорят, что ряд (2) расходится.
Частный случай числового ряда – геометрический ряд, представляющий собой сумму бесконечной геометрической прогрессии:
 . .
|
Его частичная сумма:
 . .
|
При этом если  , то геометрическая прогрессия называется бесконечно убывающей, и геометрический ряд имеет конечную сумму
, то геометрическая прогрессия называется бесконечно убывающей, и геометрический ряд имеет конечную сумму
 . .
|
В случаях, когда  , геометрический ряд расходится, т.е. конечной суммы не имеет.
, геометрический ряд расходится, т.е. конечной суммы не имеет.
|
из
5.00
|
Обсуждение в статье: Методические указания по темам |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

