 |
Главная |
Лекция 4. ЭЛЕМЕНТАРНЫЕ ДИНАМИЧЕСКИЕ ЗВЕНЬЯ И ИХ
|
из
5.00
|
ХАРАКТЕРИСТИКИ
Систему автоматического управления можно представить состоящей из ряда элементарных динамических звеньев. Под элементарными динамическими звеньями понимаются устройства, которые могут иметь различный физический вид и конструкцию, однако описываться они должны дифференциальными уравнениями не выше второго порядка. Поэтому и классифицируются элементарные динамические звенья по виду их уравнения.
Представим звено в следующем виде

Рис.4.1.
Здесь x(t) и y(t) соответственно входной и выходной сигналы.
Простейшим из звеньев является безынерционное звено, которое описывается дифференциальным уравнением нулевого порядка - алгебраическим уравнением
 ,
,
где  - безразмерный коэффициент передачи (усиления) звена.
- безразмерный коэффициент передачи (усиления) звена.
Его передаточная функция
 .
.
К безынерционным звеньям относятся различные датчики сигналов, электронные усилители, механические редукторы и т. п. Необходимо отметить, что уравнение звена не является реальным, точно отражающим характер процессов, протекающих в той или иной системе. Оно является некоторой идеальной моделью, не учитывающей инерционность датчиков или усилителей, пренебрегающей упругими свойствами и люфтами в редукторах и т. п.
Временные и частотные характеристики этого звена имеют вид
 ,
,  ;
;
 ,
,  ,
,  ,
, 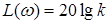 .
.
На Рис.4.2. представлены переходная характеристика безынерционного звена, а на Рис. 4.3 его ЛАЧХ при  .
.

Рис.4.2.

Рис.4.3.
Апериодическое звено (звено первого порядка) имеет следующее дифференциальное уравнение
 ,
,
где  - постоянная времени,
- постоянная времени,  - коэффициент передачи (усиления) звена. Постоянная времени имеет размерность секунд.
- коэффициент передачи (усиления) звена. Постоянная времени имеет размерность секунд.
Передаточная функция звена имеет вид
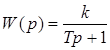 .
.
Апериодическим звеном можно описать поведение двигателя внутреннего сгорания или электродвигателя, причем если входной величиной является расход топлива (управляющее напряжение), то выходной величиной будет являться частота вращения вала двигателя. Это же звено является математической моделью электрической печи, электрического генератора постоянного тока и т. п.
Запишем частотную передаточную функцию звена
 ,
,
и его частотные и переходную характеристики
 ,
,  ,
,
 ,
,  ,
, 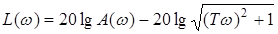 ,
,
 .
.
На Рис.4.4. изображена переходная характеристика апериодического звена при  и
и  сек.
сек.

Рис.4.4.
На Рис.4.5 и 4.6 представлены АФЧХ и ЛЧХ этого звена

Рис.4.5.

Рис.4.6.
Дифференциальное уравнение второго порядка в зависимости от величины коэффициентов имеют три звена
 ,
,
где  - постоянная времени,
- постоянная времени,  - безразмерный коэффициент демпфирования,
- безразмерный коэффициент демпфирования, 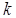 - коэффициент передачи (усиления) звена.
- коэффициент передачи (усиления) звена.
Если коэффициент демпфирования  , то звено называется колебательным, если
, то звено называется колебательным, если  звено называется консервативным, если же
звено называется консервативным, если же  - апериодическое звено второго порядка.
- апериодическое звено второго порядка.
Передаточная функция звена имеет вид

 .
.
 Запишем АФЧХ звена
Запишем АФЧХ звена

 .
.
На Рис.4.7, 4.8 и 4.9 изображены соответственно переходные характеристики, АФЧХ и ЛЧХ колебательного звена при  ,
,  ,
,  и
и  .
.


Рис.4.7.


Рис.4.8.
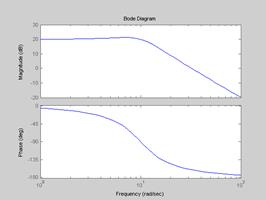

Рис.4.9.
Колебательным звеном описываются двигатели постоянного тока при некоторых значениях параметров, движение летательного аппарата относительно какой либо оси, поведение гироскопической системы и т. п.
Консервативное звено является частным случаем колебательного и описывает режим возникновения в той или иной системе незатухающих колебаний. На Рис.4.8 изображена переходная характеристика консервативного звена.

Рис.4.8.
Апериодическое звено второго порядка эквивалентно двум последовательно включенным апериодическим звеньям первого порядка.
Интегрирующее звено имеет следующее дифференциальное уравнение
 ,
,
где  - коэффициент передачи (усиления) звена.
- коэффициент передачи (усиления) звена.
Его передаточная функция
 .
.
Частотные и переходная характеристики имеют вид
 ,
,  ,
,
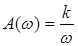 ,
,  ,
,  ,
,
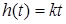 .
.
На Рис.4.9. и 4.10 представлены соответственно переходная характеристика и ЛЧХ звена

Рис.4.9.

Рис.4.10.
Примером интегрирующего звена является электродвигатель, выходной величиной которого является угол поворота вала, являющейся интегралом от угловой скорости. К интегрирующему звену можно отнести гидравлический демпфер, причем входной является сила, приложенная к поршню, а выходной величиной будет являться перемещение штока.
Для дифференцирующего звена справедливо уравнение
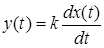 .
.
|
из
5.00
|
Обсуждение в статье: Лекция 4. ЭЛЕМЕНТАРНЫЕ ДИНАМИЧЕСКИЕ ЗВЕНЬЯ И ИХ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

