 |
Главная |
УРАВНЕНИЯ ДИНАМИКИ И СТАТИКИ
|
из
5.00
|
Динамика рассматривает состояние движения, ход развития процессов во времени. Динамика процессов обычно описывается дифференциальными или разностными уравнениями.
Будем рассматривать систему
 |
Рис.2.1.
Поведение исследуемой системы описывается дифференциальными уравнениями. Так зависимость выходного сигнала 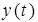 от входного
от входного 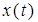 в общем случае можно описать следующим дифференциальным уравнением
в общем случае можно описать следующим дифференциальным уравнением
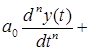
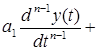 ...
... 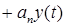
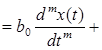
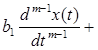 ...
... 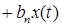 , (2.1)
, (2.1)
где
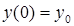 ,
, 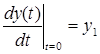 ,
, 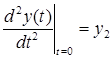 , … ,
, … , 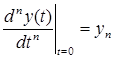 ,
,
- начальные условия. Уравнение 2.1. является уравнением динамики рассматриваемой системы.
Пусть поведение системы Рис.2.1 описывается уравнением
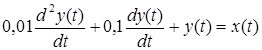 .
.
Будем предполагать, что 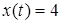 . Входной сигнал
. Входной сигнал 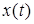 и сигнал на выходе системы
и сигнал на выходе системы 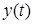 , полученный в результате моделирования при нулевых начальных условиях, изображены на Рис.2.2.
, полученный в результате моделирования при нулевых начальных условиях, изображены на Рис.2.2.
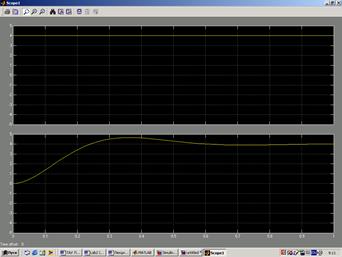
Рис.2.2.
В отличии от динамики, рассматривающей процессы протекающие в системе
во времени, статика изучает состояние покоя или равновесия. В этом случае
отсутствует временной фактор.
Из уравнения динамики (2.1), приравняв нулю все производные (так как режим установившейся), нетрудно получить уравнение статики системы
 , (2.2)
, (2.2)
где 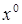 - постоянная входная величина,
- постоянная входная величина, 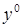 - установившееся значение выходной величины.
- установившееся значение выходной величины.
Из уравнения статики можно получить статическую характеристику системы, представляющую собой зависимость выходной величины от входной в статическом режиме
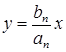 .
.
Представим статическую характеристику в виде графика Рис.2.3.
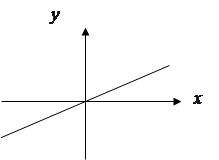
Рис.2.3.
Статическая характеристика может быть получена экспериментально путем подачи на вход системы постоянных воздействий и измерения установившихся значений выходных величин.
2.2. ЛИНЕАРИЗАЦИЯ УРАВНЕНИЙ
|

Рис.2.4.
описывается следующим дифференциальным уравнением
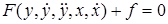 , (2.3)
, (2.3)
где 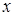 и
и 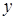 - соответственно входной и выходной сигналы,
- соответственно входной и выходной сигналы, 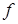 - возмущающее воздействие.
- возмущающее воздействие.
Уравнение (2.3) является нелинейным. Процесс исследования нелинейных систем существенно сложнее процесса исследования линейных. Поэтому исследование нелинейных систем стремятся свести к исследованию линейных. Процедура преобразования нелинейных уравнений в линейные называется линеаризацией.
Процедура линеаризации базируется на разложении нелинейных функций, входящих в уравнения, в ряд Тейлора. Необходимо отметить, что разложение какой либо функции в ряд Тейлора происходит в достаточно малых окрестностях некоторой точки. В качестве такой точки берется точка, соответствующая заданному режиму работы системы. В установившемся состоянии это может быть режим равновесия. Заметим, что отклонения реальных значений входных и выходных сигналов от их заданных значений в нормально работающей замкнутой автоматической системе не велико. Система работает по принципу парирования таких отклонений.
Обозначим переменные, соответствующие заданному режиму работы системы
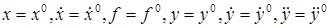 . (2.4)
. (2.4)
Введем отклонения реальных значений сигналов от требуемых
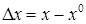 ,
, 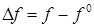 ,
, 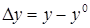 .
.
Тогда
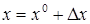 ,
, 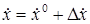 ,
, 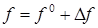 ,
, 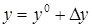 ,
, 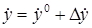 ,
, 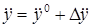 .
.
Рассматривая функцию 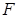 выражения (2.3) как функцию независимых переменных
выражения (2.3) как функцию независимых переменных 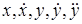 , разложим ее в ряд Тейлора в точке (2.4), соответствующей заданному режиму
, разложим ее в ряд Тейлора в точке (2.4), соответствующей заданному режиму
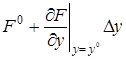 +
+ 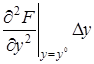 +
+ 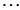 +
+ 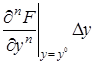 +
+
+ 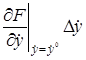 +
+ 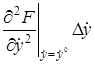 +
+ 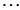 +
+ 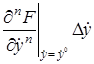 +
+
+ 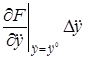 +
+ 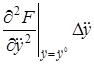 +
+ 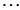 +
+ 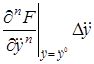 +
+
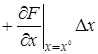 +
+ 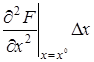 +
+ 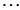 +
+ 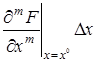 +
+
+ 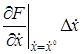 +
+ 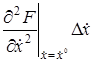 +
+ 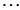 +
+ 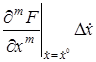 +
+ 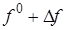 =0.
=0.
В этом выражении оставим только первые члены разложения, отбросив малые члены более высокого порядка.
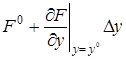 +
+ 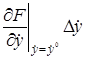 +
+ 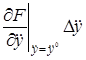 +
+
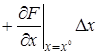 +
+ 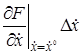 +
+ 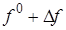 =0. (2.5)
=0. (2.5)
В заданном режиме уравнение (2.3) примет вид
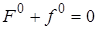 .
.
Вычтем это уравнение из (2.5), получим
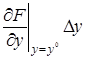 +
+ 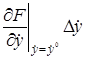 +
+ 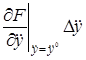
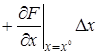 +
+ 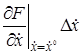
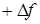 =0. (2.6)
=0. (2.6)
Введем обозначения
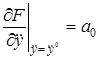 ,
, 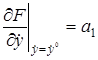 ,
, 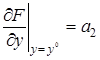 ,
, 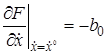 ,
, 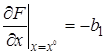 .
.
Подставив их в (2.6) и отбросив знак 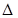 , получим линеаризованное уравнение в отклонениях
, получим линеаризованное уравнение в отклонениях
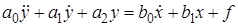 . (2.7)
. (2.7)
Линеаризация уравнения (2.3) была проведена в предположениях:
- отклонения входных 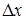 и
и 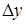 сигналов от их заданных значений малы,
сигналов от их заданных значений малы,
- функция 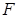 имеет непрерывные частные производные по всем своим аргументам в окрестности точки разложения, соответствующей заданному режиму,
имеет непрерывные частные производные по всем своим аргументам в окрестности точки разложения, соответствующей заданному режиму,
- линеаризованное уравнение (2.7) является уравнением в отклонениях.
|
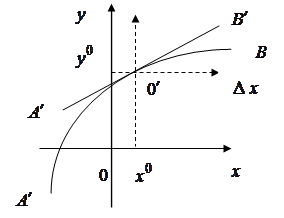 |
Рис.2.5.
В этом случае нелинейная зависимость между 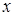 и
и 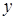 , выраженная
, выраженная
кривой 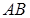 , в окрестностях точки разложения
, в окрестностях точки разложения 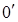 , заменена касательной
, заменена касательной 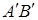 . Запись же уравнения в отклонениях, соответствует переносу начала координат в точку
. Запись же уравнения в отклонениях, соответствует переносу начала координат в точку 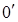 .
.
2.3. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА И ЕГО ОСНОВНЫЕ
СВОЙСТВА
Преобразованием Лапласа называется следующее соотношение
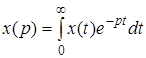 , (2.8)
, (2.8)
где 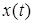 - функция вещественного переменного,
- функция вещественного переменного, 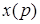 - функция комплексного переменного
- функция комплексного переменного 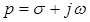 . Преобразование Лапласа ставит в соответствие функции действительного переменного
. Преобразование Лапласа ставит в соответствие функции действительного переменного 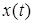 функцию комплексного переменного
функцию комплексного переменного 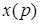 . Смысл преобразования Лапласа заключается в том, что оно переводит рассмотрение процесса, являющегося функцией действительного переменного, например времени, на комплексную плоскость с координатами
. Смысл преобразования Лапласа заключается в том, что оно переводит рассмотрение процесса, являющегося функцией действительного переменного, например времени, на комплексную плоскость с координатами 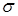 и
и 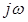 .
.
Функцию 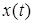 называют оригиналом, а функцию
называют оригиналом, а функцию 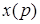 изображением по Лапласу или просто изображением. Преобразование Лапласа можно записать в символическом виде
изображением по Лапласу или просто изображением. Преобразование Лапласа можно записать в символическом виде
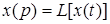 (2.9)
(2.9)
где 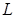 - оператор Лапласа.
- оператор Лапласа.
Функция 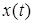 , являющаяся оригиналом, должна обладать следующими свойствами:
, являющаяся оригиналом, должна обладать следующими свойствами:
- должна быть определена и кусочно-дифференцируема на всей положительной числовой полуоси 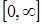 ;
;
- 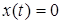 при
при 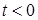 ;
;
- существуют такие положительные числа 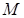 и
и 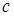 , что
, что 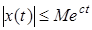 при
при 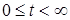 .
.
С помощью обратного преобразования Лапласа
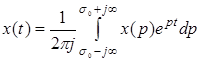 , (2.10)
, (2.10)
можно найти по известному изображению его оригинал. В нем интеграл берется вдоль любой прямой 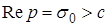 . Символически обратное преобразование Лапласа можно записать
. Символически обратное преобразование Лапласа можно записать
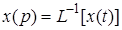 ,
,
где 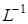 - обратный оператор Лапласа.
- обратный оператор Лапласа.
Рассмотрим основные свойства преобразования Лапласа.
1. Свойство линейности. Для любых постоянных 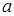 и
и 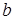
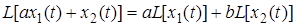 .
.
2. Дифференцирование оригинала.
Для первой производной
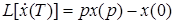 , где
, где 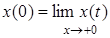 .
.
Для n-й производной
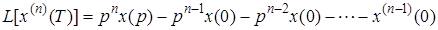 ,
,
где
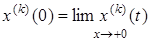 ,
, 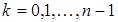 .
.
Если начальные условия нулевые
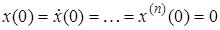 ,
,
то
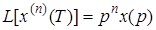 .
.
Таким образом, n-кратное дифференцирование оригинала при нулевых начальных условиях, соответствует умножению изображению на n-ю степень 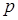 .
.
3. Интегрирование оригинала сводится к делению изображения на 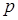 .
.
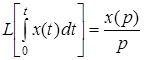 .
.
4. Теорема запаздывания. Для любого положительного 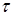
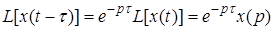 .
.
5. Теорема о свертке. Если 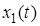 и
и 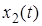 - оригиналы, а
- оригиналы, а 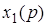 и
и 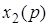 - их изображения, то
- их изображения, то
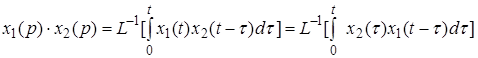 .
.
Интеграл правой части называется сверткой функций 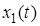 и
и 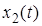 , который обозначают
, который обозначают 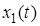 *
* 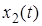
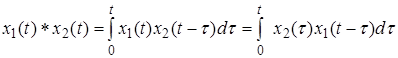 .
.
6. Теорема о предельных значениях. Если 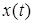 - оригинал, а
- оригинал, а 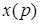 - его изображение, то
- его изображение, то
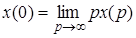 ,
,
и при существовании предела 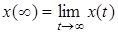 ,
,
справедливо записать
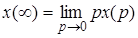 .
.
2.4. Запись дифференциальных уравнений в символическом виде.
Будем рассматривать следующую систему
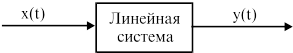
Рис.2.6
Пусть в общем случае линейная система описывается дифференциальным уравнением n-го порядка
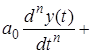
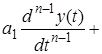 ...
... 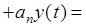
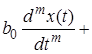
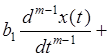 ...
... 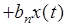 ,
,
где 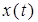 и
и 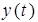 соответственно входной и выходной сигналы системы. Преобразуем левую и правую части этого уравнения по Лапласу. В результате получим следующее дифференциальное уравнение в символическом виде
соответственно входной и выходной сигналы системы. Преобразуем левую и правую части этого уравнения по Лапласу. В результате получим следующее дифференциальное уравнение в символическом виде
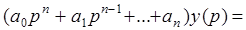
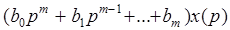 , (2.11)
, (2.11)
где 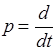 - оператор дифференцирования.
- оператор дифференцирования.
Введем обозначения
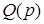 =
= 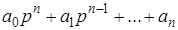 ,
,
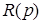 =
= 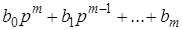 .
.
Тогда уравнение (2.11) можно записать в более компактно
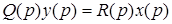 .
.
2.5. C тандартная форма записи линейных дифференциальных
уравнений
Принято, что линейные дифференциальные уравнения не выше второго порядка записываются в стандартной форме, а именно:
- члены уравнения, содержащие выходную величину и ее производные, записываются в левой части уравнения;
- все остальные члены уравнения, записываются справа;
- коэффициент при выходной величине делают равным единице;
- коэффициенты при входных и выходных величинах и их производных являются либо постоянными времени, либо коэффициентами передачи (усиления).
Рассмотрим дифференциальное уравнение в символическом виде
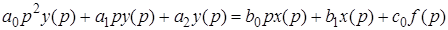 .
.
Разделим обе части этого уравнения на 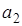 и введем обозначения
и введем обозначения
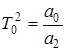 ,
, 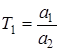 ,
, 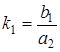 ,
, 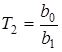 ,
, 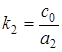 .
.
Тогда
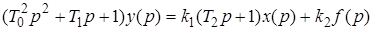 .
.
Здесь 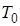 ,
, 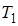 ,
, 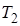 - имеют размерность времени и называются постоянными времени,
- имеют размерность времени и называются постоянными времени, 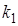 и
и 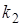 - безразмерные коэффициенты передачи (усиления).
- безразмерные коэффициенты передачи (усиления).
2.5. Передаточные функции.
Передаточной функцией системы называется отношение выходного сигнала к входному, преобразованных по Лапласу при нулевых начальных условиях. Тогда передаточная функция рассматриваемой системы (Рис.2.6) равна
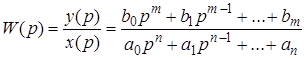 . (2.12)
. (2.12)
Рассмотрим систему
 |
Рис.2.7.
Пусть ее поведение описывается следующим дифференциальным уравнением в символической записи
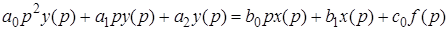 ,
,
иначе
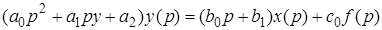 .
.
Приведем это уравнение к виду
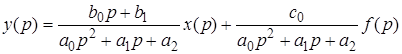 .
.
Введем обозначения
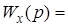
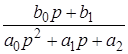 ,
,
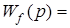
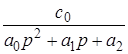 .
.
Здесь
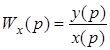 - передаточная функция по входному сигналу,
- передаточная функция по входному сигналу,
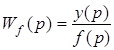 - передаточная функция по возмущающему воздействию.
- передаточная функция по возмущающему воздействию.
Если линейная система имеет несколько входов, то при определении передаточной функции по одному из входов, другие входы полагаются равными нулю.
|
из
5.00
|
Обсуждение в статье: УРАВНЕНИЯ ДИНАМИКИ И СТАТИКИ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

