Корней характеристического уравнения на комплексной плоскости

Пусть система описывается следующим дифференциальным уравнением в операторном виде

            (1)

Здесь - оператор дифференцирования, 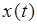- входное воздействие, - выходная величина.

    Решение уравнения (1) представим в виде

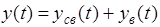                                            ,                                       (2)

где - свободная составляющая решения, которая определяется решением однородного дифференциального уравнения (1) без правой части

                               ,                            (3)

- вынужденная составляющая решения, определяется как частное решение неоднородного дифференциального уравнения

                     (4)

В соответствии с определением устойчивости по А.М. Ляпунову, система, описываемая уравнением (1) будет асимптотически устойчивой, если при  свободная составляющая , определяемая решением дифференциального уравнения (3), будет стремиться к .

    Решение дифференциального уравнения (3) ищут в виде

                                                 .                                              (5)

Продифференцировав это выражение 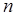 раз, подставив результаты дифференцирования в (3) и сократив на общий множитель , получим

                                          .                                 (6)

Данное алгебраическое уравнение носит название характеристического уравнения. Формально оно может быть получено из левой части уравнения системы (1) при входном воздействии

                                   .                                    (7)

Следует заметить, что в этом уравнении  не является символом дифференцирования, так как 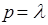. Таким образом (7) является характеристическим уравнением исследуемой системы, а его корни определяют характер переходных процессов в системе

                                              .                                           (8)

В этом решении - корни характеристического уравнения, - постоянные интегрирования, определяемые из начальных условий.

    Полагая, что 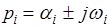 и используя известную формулу Эйлера

                                  ,                                  (9)

решение (8) может быть представлено в следующем виде

                                    ,                            (10)

где  и  - новые постоянные интегрирования. Из этого решения следует, что на устойчивость системы влияет знак вещественной части корней характеристического уравнения . Если характеристическое уравнение имеет хотя бы один корень с вещественной частью , то при  переходной процесс будет расходящимся и только когда у всех корней , то при  переходный процесс будет затухающим. Наличие мнимой части в корне 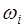 говорит о присутствии составляющей в решении (10) колебательного характера. Если при этом , то при  в системе имеют место незатухающие колебания, если   или 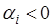, то в системе будут соответственно расходящиеся и затухающие колебания.

    Необходимое и достаточное условие устойчивости формулируется следующим образом: для того чтобы линейная система была асимптотически устойчива, необходимо и достаточно, чтобы все корни ее характеристического уравнения имели отрицательные вещественные части, иначе располагались в левой полуплоскости корней.

    Например для системы, имеющей характеристическое уравнение

                           ,

корни на комплексной плоскости корней располагаются следующим образом

                        

Здесь по оси ординат откладывается вещественная часть корня, а по оси абсцисс его мнимая часть. Как видно из Рис.1. все пять корней полинома расположены в левой полуплоскости, причем 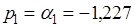- действительный корень, а 

                                

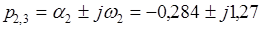
 и

                                ,

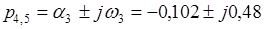 комплексно-сопряженные корни. Таким образом рассматриваемая система устойчива.

    На Рис.2 изображен переходной процесс, полученный в Mathcad 7. Как следует из графика переходной процесс является затухающим.

                        

Обычно корни с отрицательными вещественными частями называют левыми, а корни с положительными вещественными частями - правыми. Если система имеет хотя бы один правый корень, то она неустойчива. Если корень является мнимым, то есть расположен на мнимой оси плоскости корней, то система находится на границе устойчивости.

    Исследование линейных систем на устойчивость с помощью

                                        алгебраических критериев                   

Алгебраические критерии устойчивости позволяют судить об устойчивости линейных систем по значениям коэффициентов характеристического уравнения

                                   

                              .                                   (1)

Нетрудно показать, что необходимым (но не достаточным) условием устойчивости является положительность всех коэффициентов характеристического уравнения

                            .                                    (2)

Заметим, что если все коэффициенты характеристического уравнения отрицательны, то умножив их на -1, получим все положительные коэффициенты.

Если выполняется условие (2), то исследуемая система может быть устойчивой, а может быть и неустойчивой. Однако если условие (2) не выполняется, то система обязательно будет неустойчивой. Докажем это.

    Предположим, что все корни характеристического уравнения вещественные. Тогда уравнение (1) можно представить в следующем виде

                                 ,                             (3)

где - корни характеристического уравнения. Будем предполагать, что . Если это не так, то умножим (1) на -1.

    Для устойчивой системы все вещественные корни должны быть отрицательными, поэтому  и т.д. Тогда (3) примет вид

                                .                            (4)

Раскрыв в (4) скобки, получим уравнение, аналогичное (1) в котором все коэффициенты положительны.

    Теперь предположим, что уравнение (1) будет иметь комплексные корни с отрицательными вещественными частями. В этом случае результат не изменится, так как если 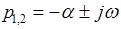, то сомножители в уравнении (3) будут иметь вид

                        .

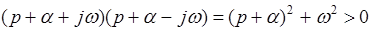Следовательно и в этом случае все коэффициенты в (1) будут больше 0.

    Необходимо отметить, что для систем, имеющих характеристическое уравнение первого и второго порядка, необходимое условие устойчивости является и достаточным.

    К алгебраическим критериям устойчивости относятся: - критерий, полученный в 1877 г. английским математиком Э. Раусом; - критерий, разработанный в 1895 г. немецким ученым А. Гурвицем; - критерий, предложенный в 1914 г. П. Льенаром и Р. Шипаром. Наиболее удобным с точки зрения использования ЭВМ является критерий устойчивости Гурвица (для систем, имеющих порядок характеристического уравнения  его модификацию - критерий Льенара-Шипара), который позволяет по определителям, составленным из коэффициентов характеристического уравнения системы судить об ее устойчивости.

Пусть исследуемая система имеет следующее характеристическое уравнение

                          .                               (5)

Из коэффициентов этого уравнения находят главный определитель Гурвица

                    .

По главной диагонали определителя слева направо записываются коэффициенты характеристического уравнения (5), начиная с  по . В столбцы вверх от главной диагонали записываются коэффициенты в порядке возрастания индексов, а в столбцы вниз - коэффициенты в порядке убывания индексов. Если при этом индекс коэффициента становится больше 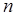 - порядка характеристического уравнения и меньше 0, то данный коэффициент приравнивается 0.

    Из главного определителя получают все  определителей Гурвица в следующем виде

                        и т. д.

    Формулировка критерия устойчивости Гурвица такова: для того чтобы система была устойчивой необходимо и достаточно, чтобы при  были больше нуля все  определителей Гурвица.

    Необходимо отметить, что -й определитель Гурвица может быть выражен через ( )-й следующим образом

                                                     .

Однако в устойчивой системе  и должно быть выполнено необходимое условие устойчивости, заключающееся в положительности всех коэффициентов характеристического уравнения, в том числе и , а значит и . Следовательно последний -й определитель в критерии Гурвица можно не находить.

    Заметим, что когда все коэффициенты характеристического уравнения положительны и положительны все определители Гурвица с нечетными индексами, то оказываются положительными также все определители Гурвица с четными индексами, и наоборот. Откуда следует формулировка критерия Льенара-Шипара: если все коэффициенты характеристического уравнения положительны, то для устойчивости системы необходимо и достаточно, чтобы среди определителей Гурвица были положительны все определители с четными (нечетными) индексами.

 

 

    Исследование линейных систем на устойчивость с помощью

                                              критерия Михайлова

       Критерий устойчивости Михайлова относится к частотным критериям в основе которых лежит принцип аргумента, заключающийся в следующем. Известно, что характеристический полином системы

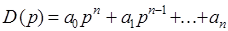                                                                           (1)

может быть представлен в виде

                               ,                        (2)

где  - корни характеристического уравнения

                                     .                                  (3)

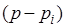Рассмотрим -й сомножитель в (2)  и представим его на комплексной плоскости. Корень  может быть изображен в виде вектора, проведенного из начала координат в точку , причем длина вектора равна его модулю, то есть , а угол, образованный с положительным направлением действительной оси - аргументу комплексного числа , то есть  (Рис.1).

                             

 

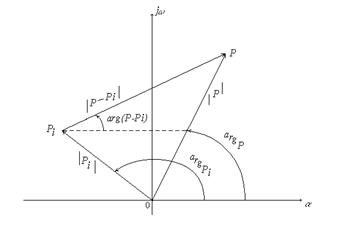
                                                           Рис.1.

Аналогично на комплексной плоскости может быть изображен и вектор , проведенный в произвольную точку этой плоскости. Тогда сомножитель  представим в виде разности двух рассмотренных векторов. В частном случае при , где  представляет собой частоту колебаний, соответствующих мнимому корню характеристического уравнения, характеристический полином примет вид

                        .                  (4)

Тогда концы векторов  будут располагаться на мнимой оси в точке  (Рис.2).

   

 

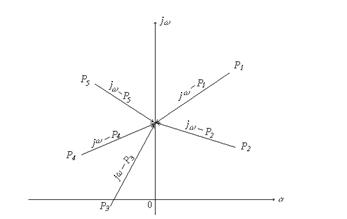
                                                           Рис.2.

Необходимо отметить, что в (4)  представляет собой вектор, модуль которого равен

                           ,                    (5)

и аргумент

        .   (6)

При изменении частоты  каждый элементарный вектор  в (4) будет поворачиваться, изменяя и модуль  в соответствии с (5) и фазу (аргумент)  в соответствии с (6). Считая поворот вектора против часовой стрелки положительным, при изменении  от  до  каждый элементарный вектор в (4) повернется на угол + , если его начало координат, то есть корень , расположено слева от мнимой оси, и на угол - , если корень расположен справа от мнимой оси. Такой поворот элементарных векторов 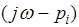 и  изображен на Рис.3.

         

 

                                                          Рис.3.

    Если характеристический полином имеет 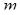 правых и  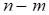левых корней, то при изменении  от  до  вектор  повернется на угол, равный сумме поворотов элементарных векторов , то есть изменение аргумента равно

                   .              (7)

Сформулируем принцип аргумента: изменение аргумента  при изменении частоты  от  до  равно разности между числом левых и правых корней характеристического уравнения, умноженной на .

При изменении  от 0 до  изменение аргумента вектора  будет вдвое меньше

                      .                                 (8)

В 1936 г. на основании принципа аргумента (8) А.В. Михайловым был сформулирован следующий критерий устойчивости: для того чтобы система  - го порядка была устойчива, необходимо и достаточно, чтобы вектор , описывающий кривую Михайлова, при изменении частоты  от 0 до  повернулся вокруг начала координат против часовой стрелки, нигде не обращаясь в 0 на угол .

Заметим, что кривая (годограф) Михайлова для устойчивых систем всегда должна начинаться на вещественной положительной полуоси, поскольку при  и  из (1) следует, что  на основании необходимого условия устойчивости.

Для построения кривой Михайлова необходимо представить характеристический полином в виде

                             ,

где - вещественная, а - мнимая функции Михайлова и строить кривую Михайлова на комплексной плоскости с осью ординат  и осью абсцисс .

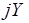    Для устойчивых систем кривая Михайлова имеет плавную спиралевидную форму и уходит в бесконечность в том квадранте координатной плоскости, номер которого равен порядку характеристического уравнения. На Рис.4 изображены кривые Михайлова, соответствующие устойчивым системам, а на Рис.5 - кривые неустойчивых систем.

          

 

 

                                                         Рис.4.

                           

                                                          Рис.5.