 |
Главная |
Суммируя по известной формуле эту прогрессию, получаем
|
из
5.00
|
Мера ограниченного открытого множества
В теории функций вещественной переменной большую роль играет понятие меры точечного множества, обобщающее понятие длины промежутка, площади прямоугольника, объема параллелепипеда и т.д. В этой главе мы изложим теорию измерения линейных ограниченных точечных множеств, принадлежащую А.Лебегу.
Так как наиболее простой структурой обладают открытые множества, то естественно начать именно с них.
Определение 1. Мерой интервала ( a, b) называется его длина, т.е. b - a. Это число обозначается так:
m (a, b) = b - a
Очевидно, что всегда m ( a, b) > 0 .
Лемма 1. Если в интервале D содержится конечное число взаимно не налегающих интервалов d1, d2, ..., dn, то

Д о к а з а т е л ь с т в о. Пусть D = (A, B), dk = (ak, bk) (k = 1, 2, …, n).
Не нарушая общности, можно считать, что интервалы dk перенумерованы в порядке возрастания левых концов, т.е. что
a1 < a2 < … < an.
Но тогда, очевидно, bk £ ak+1 (k = 1, 2, …, n - 1), ибо иначе интервалы dk и dk+1 налегали бы друг на друга. Поэтому сумма
Q = (B - bn) + (an - bn-1) + … + (a2 - b1) + (a1 - A)
не отрицательна. Но очевидно, что 
 , откуда и следует лемма.
, откуда и следует лемма.
Следствие. Если на интервале D лежит счетное множество взаимно не налегающих интервалов d k ( k = 1, 2, 3, …), то
 .
.
[Имея дело с положительным расходящимся рядом, мы приписываем ему сумму, равную + ¥; поэтому всякий положительный ряд имеет некоторую сумму. Неравенства  k< C (положительного ряда) гарантирует его сходимость.]
k< C (положительного ряда) гарантирует его сходимость.]
Определение 2. Мерой mG непустого открытого ограниченного множества G называется сумма длин всех его составляющих интервалов dk:
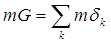
(Не зная, конечно или счетно множество {dk}, мы будем употреблять обозначение  dk, подразумевая, смотря по обстоятельствам, под этим символом
dk, подразумевая, смотря по обстоятельствам, под этим символом 
 k или
k или  k.)
k.)
В силу вышеотмеченного следствия,
mG < + ¥
Если множество G пусто, то мы , по определению, полагаем
mG =0,
так что всегда mG³0.
Если D есть интервал, содержащий в себе открытое множество G, то
mG £ m D ,
что вытекает из того же следствия.
Пример (Канторово множество G 0 ). Построение Канторова множества G0 состояло из ряда последовательных шагов.
На первом шагу брался  интервал (1/3, 2/3) длины 1/3. На втором шагу к нему присоединялись два интервала: (1/9, 2/9) и (7/9, 8/9), длины 1/9 каждый.
интервал (1/3, 2/3) длины 1/3. На втором шагу к нему присоединялись два интервала: (1/9, 2/9) и (7/9, 8/9), длины 1/9 каждый.
На третьем шагу присоединялись еще четыре интервала, длины 1/27 каждый и т.д.
Таким образом
mG 0 =  …
… 
Суммируя по известной формуле эту прогрессию, получаем
mG 0 = 1.
Теорема 1. Пусть G 1 и G 2 два ограниченных открытых множества. Если G 1 Ì G 2 , то
mG 1 £ mG 2.
Д о к а з а т е л ь с т в о. Пусть d i (i = 1, 2, …) и Dk (k = 1, 2, …) суть, соответственно, составляющие интервалы множеств G1 и G2.
В силу теоремы 4, § 5, гл.II, каждый из интервалов di содержится в одном (и только одном) из интервалов Dk.
Поэтому множество {di} можно разбить на ряд взаимно не пересекающихся подмножеств А1, А2, А3,…, относя di в Аk в том случае, когда di Ì Dk.
Тогда, пользуясь известными свойствами двойных рядов, мы можем написать
 .
.
Но, в силу следствия леммы 1,
 , откуда
, откуда  ,
,
что и требовалось доказать.
Следствие. Мера открытого ограниченного множества G есть точная нижняя граница мер всевозможных открытых ограниченных множеств, содержащих G .
Теорема 2. Если открытое ограниченное множество G является суммой конечного числа или счетного множества взаимно не налегающих открытых множеств
 ,
,
то
 .
.
Это свойство меры называется полной аддитивностью.
Д о к а з а т е л ь с т в о. Пусть  (i = 1, 2, …) суть составляющие интервалы множества Gk. Покажем, что каждый из них является составляющим интервалом суммы G.
(i = 1, 2, …) суть составляющие интервалы множества Gk. Покажем, что каждый из них является составляющим интервалом суммы G.
В самом деле, то обстоятельство, что  G, очевидно. Остается убедиться, что концы интервала
G, очевидно. Остается убедиться, что концы интервала  не принадлежат G. Допустим, что, например, правый конец интервала
не принадлежат G. Допустим, что, например, правый конец интервала 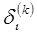 принадлежит G. Тогда этот правый конец (обозначим его через m) должен принадлежать какому-нибудь из слагаемых множеств. Пусть m Î Gk'. (Очевидно k¢ ¹ k, ибо множеству Gk точка m заведомо не принадлежит.) Но множество Gk¢ открыто и, стало быть, точка m принадлежит одному из составляющих интервалов этого множества m Î di¢(k¢). Однако это влечет за собой то, что интервалы di(k) и di¢(k¢) пересекаются, последнее же противоречит условию Gk Gk¢= 0.
принадлежит G. Тогда этот правый конец (обозначим его через m) должен принадлежать какому-нибудь из слагаемых множеств. Пусть m Î Gk'. (Очевидно k¢ ¹ k, ибо множеству Gk точка m заведомо не принадлежит.) Но множество Gk¢ открыто и, стало быть, точка m принадлежит одному из составляющих интервалов этого множества m Î di¢(k¢). Однако это влечет за собой то, что интервалы di(k) и di¢(k¢) пересекаются, последнее же противоречит условию Gk Gk¢= 0.
Итак, действительно, каждый из di(k) есть составляющий интервал множества G. С другой стороны, каждая точка G принадлежит хоть одному di(k) . Наконец, все эти интервалы различны. Таким образом, множество
 (i = 1, 2, …; k = 1, 2, …)
(i = 1, 2, …; k = 1, 2, …)
есть множество всех составляющих интервалов суммы G.
Установив это, уже легко закончить доказательство:

 =
= 

что и требовалось доказать.
Для того чтобы перенести теорему (соответственно изменить ее) на случай суммы п е р е с е к а ю щ и х с я слагаемых, нам понадобятся две простые леммы.
Лемма 2. Пусть сегмент [P, Q] покрыт конечной системой Н интервалов (l, m ). Тогда


Д о к а з а т е л ь с т в о. Выделим из системы Н некоторую ее часть Н*, которая строится следующим образом: обозначим через (l1,  ) какой-нибудь из интервалов системы H, содержащих точку P
) какой-нибудь из интервалов системы H, содержащих точку P
l1 < P < m1
(хоть один такой интервал существует). Если окажется, что m1>Q, то интервал (l1, m1) , и составляет требуемую систему H* . Если же m1 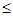 Q, то m1Î[P, Q], и можно в системе H найти интервал ( l2, m2), содержащий точку m1 ,
Q, то m1Î[P, Q], и можно в системе H найти интервал ( l2, m2), содержащий точку m1 ,
l2 < m1 < m2
Если окажется, что m2>Q, то процесс окончен, и интервалы (l1, m1) и ( l2, m2) и составляют систему Н*.
Если же m2 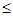 Q, то m2Î[P, Q], и можно в системе H найти интервал ( l3, m3), содержащий m2.
Q, то m2Î[P, Q], и можно в системе H найти интервал ( l3, m3), содержащий m2.
l3 < m2 < m3
Если m3>Q, то процесс закончен, а если m3 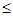 Q, то продолжаем наш процесс.
Q, то продолжаем наш процесс.
Но ведь множество H по условию конечно, а наш процесс состоит в выделении из H все новых и новых интервалов, ибо
m1 < m2 < m3 < …
Поэтому процесс обязательно должен закончится, а конец его состоит в том, что какая-то из точек mk окажется лежащей правее точки Q.
Пусть mn>Q, но mn-1£Q, т.е. процесс заканчивается после n-го шага.
Тогда интервалы (l1, m1), ( l2, m2), … , (ln, mn) и составляют систему H. При этом lk+1<mk (k = 1, 2, … , n-1).
Значит

а так как mn - l1 > Q – P, то Q – P <  , откуда и подавно
, откуда и подавно
Q – P <  .
.
Лемма 3. Пусть интервал D есть сумма конечного или счетного множества открытых множеств
D =  .
.
Тогда
mD 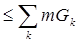 .
.
Д о к а з а т е л ь с т в о. Пусть D = (A, B) и пусть составляющие интервалы множества Gk суть di(k) (i = 1, 2, …).
Возьмем положительное число e (0 < e <  ) и рассмотрим сегмент
) и рассмотрим сегмент  , содержащийся в интервале D.
, содержащийся в интервале D.
Этот сегмент покрыт системой интервалов di(k) (i = 1, 2, …; k = 1, 2, …). Применяя к этой системе теорему Бореля о конечном покрытии из § 2, гл. II, мы получим некоторую конечную систему
 (s = 1, 2, … n),
(s = 1, 2, … n),
покрывающую сегмент  . В силу предыдущей леммы,
. В силу предыдущей леммы,  , откуда и подавно
, откуда и подавно
B – A - 2e <  .
.
Так как число e произвольно мало, то
B – A  ,
,
и лемма доказана.
Теорема 3. Если открытое ограниченное множествоG является суммой конечного числа или счетного множества открытых множеств Gk, G =  , то
, то
mG 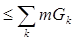 .
.
Д о к а з а т е л ь с т в о. Пусть Di (i = 1, 2, …) суть составляющие интервалы суммы G. Тогда mG =  .
.
Но  откуда, в силу леммы 3,
откуда, в силу леммы 3,  и, стало быть,
и, стало быть,
 (*)
(*)
С другой стороны 
При этом (что является здесь основным) отдельные слагаемые правой части взаимно не пересекаются (потому что  при i¹i`). Значит, мы находимся в условиях применимости теоремы 2, а потому
при i¹i`). Значит, мы находимся в условиях применимости теоремы 2, а потому
 (**)
(**)
Сопоставляя (*) и (**), мы и получаем теорему.
|
из
5.00
|
Обсуждение в статье: Суммируя по известной формуле эту прогрессию, получаем |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

