Отметим теперь легко проверяемое включение

G-F (G_k-F_k).

Все входящие сюда множества открыты и ограничены, так что, на основании теорем § 1, мы имеем

m(G-F)

или

mG - mF <e.

Отсюда и из (*) вытекает, что m*E - m_*E<e, а также как e сколь угодно мало, то

m*E = m_*E.

Теорема 6. Пересечение конечного числа измеримых множеств измеримо.

Д о к а з а т е л ь с т в о. Пусть E= , причем множества E_k  измеримы. Назовем через D какой-нибудь интервал, содержащий все множества E_k. Легко проверить, что C_DE= .

Но множества С E_k измеримы одновременно с множествами E_k, откуда, в силу теоремы 5, следует измеримость множества C_DE, а с ним и множества E, что и требовалось доказать.

Теорема 7. Разность двух измеримых множеств измерима.

Д о к а з а т е л ь с т в о. Пусть E = E₁ - E₂, где множества E₁ и E₂ измеримы. Назовем через D какой-нибудь интервал, содержащий оба множества E₁ и E₂. Тогда E=E₁·C_DE₂ и дело сводится к предыдущей теореме.

Теорема 8. Если в условиях теоремы 7 будет E ₁ E ₂ , то

ME = mE₁ - mE₂.

Д о к а з а т е л ь с т в о. Очевидно E₁=E+E₂ (EE₂=0), откуда, в силу теоремы 4, mE₁=mE+mE₂, что равносильно теореме.

Теорема 9. Если ограниченное множество E является суммой счетного множества измеримых множеств, то E измеримо.

Д о к а з а т е л ь с т в о. Пусть E= .

Введем множества A_k (k=1, 2, …), полагая

A₁=E₁, A₂=E₂-E₁, …, A_k=E_k-(E₁+…+E_k-1), …

Легко проверить, что . При этом все множества A_k измеримы и попарно не пересекаются (в последнем вся суть доказательства), так что дело свелось к теореме 4.

Условие ограниченности множества Е (которое в теореме 5 выполнялось само собой) отбросить нельзя, как видно хотя бы из примера Е_k = [0, k], где сумма _k = [0, + 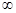) неизмерима.

Теорема 10. Пересечение счетного множества измеримых множеств измеримо.

Д о к а з а т е л ь с т в о. Пусть _k, где все множества Е_k измеримы. Так как Е Е₁, то множество Е ограничено. Обозначим через D  какой-нибудь интервал, содержащий это множество, и положим А_k= D Е_k   (k=1, 2, 3, …).

Тогда

_k= _k)= _k.

Легко проверить, что 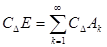, и дело сводится к теоремам 3 и 9.

В заключение установим две теоремы, играющие важную роль в теории функций.

Теорема 11. Пусть множества Е₁, Е₂, Е₃, … измеримы. Если

и если сумма ограничена, то

[mE_n].

Д о к а з а т е л ь с т в о. Легко видеть, что множество Е можно представить в форме

Е=Е₁ + (Е₂ – Е₁) + (Е₃ – Е₂) + (Е₄ – Е₃) + …,

где отдельные слагаемые попарно не пересекаются. Отсюда, в силу теорем 4 и 8, следует, что

На основании самого определения суммы бесконечного ряда, последнее равенство можно переписать так

{

а это равносильно теореме, ибо

mE₁+ 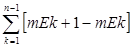=mE_n

Теорема 12. Пусть E ₁ , E _2, E ₃ ,… суть измеримые множества, и Е= . Если Е₁ É E₂ É E₃ É _…, то

mE = lim .

Д о к а з а т е л ь с т в о . Эту теорему легко свести к предыдущей. Действительно, обозначив через D какой-нибудь интервал, содержащий множество Е₁, мы будем иметь

С_DE₁ÌC_DE₂ÌC_DE₃Ì ..., C_DE= .

В силу теоремы 11 мы получаем, что

m(С_DE)=

что можно представить и так:

mD - mE=

а это равносильно теореме.

 

 

Измеримость и мера как инварианты движения

 

Пусть даны два множества А и В, состоящие из объектов любой природы. Если указано правило, которое каждому элементу а множества А ставит в соответствие один и только один элемент b множества В, то говорят, что установлено однозначное отображение множества А в множество В. При этом не предполагается, что каждый элемент множества В оказывается соотнесенным какому-нибудь элементу из А. Понятие отображения есть прямое обобщение понятия функции. В связи с этим элемент b Î В, отвечающий элементу а Î A, часто обозначают через f(а) и пишут b=f (а).

Если b=f(а), то мы будем называть элемент b образом элемента а, а элемент а прообразом элемента b. При этом один элемент b может иметь несколько прообразов.

Пусть А* есть часть множества А, а В* есть множество образов всех элементов А* (иначе говоря, если аÎА*, то f(а) ÎВ*, и если bÎВ*, то существует хоть один элемент аÎА* такой, что f(а) = b). В таком случае множество В* называется образом множества А*, что записывают так: В*= f(А*).

При этом множество А* называется прообразом множества В*.

Установив эти общие понятия, перейдем к рассмотрению одного важного специального вида отображений.

 Определение 1. Однозначное отображение j (х) числовой прямой Z в себя называется движением, если расстояние между образами любых двух точек прямой равно расстоянию между самими этими точками:

 ½j (х) - j (y)½= ½ х – y ½.

 Иначе говоря, движением называется такое отображение множества Z в множество Z, которое не изменяет расстояний между точками Z.

 В определение понятия движения не включено требование, чтобы каждая точка Z cлужила образом какой-нибудь точки, а также требование, чтобы разные точки Z имели разные же образы. Однако оба эти обстоятельства имеют место. Убедимся в этом пока для одного из них.

 Теорема 1. Пусть j ( х) есть движение. Если х ¹ y , то j ( х) ¹ j ( y ).

 Действительно, в этом случае ½j (х) - j (y) ½ =  ½х - y½¹ 0.

 Теорема 2. a ) Если А Ì В, то j ( А) Ì j ( В).

                b )

                c )

                d ) Если L пустое множество, то j ( L ) = L

Доказательство предоставляется читателю; укажем лишь на то, что при доказательстве с) используется теорема 1.

Легко проверить, что следующие три отображения являются движениями:

I . j ( х) = х + d (сдвиг),

II . j ( х) = - х (зеркальное отражение),

III . j ( х) = - х + d .

Чрезвычайно важным является то, что этими тремя (собственно – двумя, ибо III охватывает II) типами исчерпываются все возможные движения в Z.

     Теорема 3. Если j ( х) есть движение, то либо

          j ( х) = х + d ,

либо

          j ( х) = - х + d .

Д о к а з а т е л ь с т в о . Положим, j (0) = d. Тогда для всякого х будет | j (х) – d | = | х | и, стало быть,

j ( х ) = (-1) ^{s( х )} х + d               [s(х) = 0, 1].

Функция s (х) определена для всякого х ¹ 0. Нашей задачей является установление того, что s (х) есть постоянная величина.

Пусть x и y две точки, причем x ¹ 0, y ¹ 0, x ¹ y. Тогда

j (x) - j (y) = (-1) ^{s (x)} x – (-1) ^{s (y)} y,

или

j (x) - j (y) = (-1) ^{s (x)} [x – (-1) ^r y],

где r = s (y) - s (x) имеет одно из трех значений r = 1, 0, -1.

Пользуясь определением движения, можно утверждать, что

| x – (-1) ^r y| = | x - y|.

Отсюда, либо x – (-1)^r y = x – y, либо же x – (-1)^r y = -x + y.

Но второй случай невозможен, ибо он приводит к тому, что

2x = y [1 + (-1) ^r ], откуда (при r = ± 1) x = 0, или (при r = 0) x = y, а это противоречит условию.

Значит, остается первый случай, который дает, что r = 0, т.е. s(x) = s(y).

Значит, для всех x ¹ 0 функция s (x) имеет одно и то же значение

s (x) = s (s = 0, 1), так что j (x) = (-1) ^s x + d.

Поскольку это равенство, очевидно, остается в силе и для x = 0, теорема доказана.                                                                                                                                                                                                                                                                                                                                                                                                                                                                                       

Следствие. При движении каждая точка y Î Z служит образом некоторой точки x Î Z , т.е. j ( Z ) = Z .

Действительно, если j (x) = (-1) ^s x + d, то прообразом точки y служит точка x = (-1) ^s (y-d).

Если j (x) = (-1) ^s x + d есть некоторое движение, то движение   

j^-1 (x) = (-1) ^s (x – d)

называется обратным движением. Эти два движения связаны соотношениями                             

j [j^-1 (x)] = j^-1[j (x)] = x.

Иначе говоря, если точка х в движении j имеет образом точку y, то в движении j^-1 точка y имеет образом точку х. Весьма важным является то, что для всякого движения существует обратное ему движение.

Теорема 4. При движении: а) всякий интервал переходит в интервал той же меры, причем концами интервала-образа служат образы концов интервала-прообраза;

b ) образ ограниченного множества есть ограниченное же множество.

Д о к а з а т е л ь с т в о. Пусть D = (a, b) есть некоторый интервал. Тогда при движении j (x) = x + d образом интервала D служит интервал (а+ d, b + d), а при движении j (x) = -x + d – интервал (d – b, d – a). В обоих случаях mj (D) = b – a = mD.

Чтобы доказать b), обозначим через Е какое-нибудь ограниченное множество. Если D есть интервал, содержащий множество Е, то

j (Е) Ì j (D), так что j (Е) ограничено. Можно рассуждать и так: если для всех х из Е будет | х | < k, то для всех у из j(E) будет | у|<k+|d|.

Теорема 5. При движении: а) замкнутое множество переходит в замкнутое множество;       

b ) открытое множество переходит в открытое множество.

Д о к а з а т е л ь с т в о. a) пусть j (F) есть образ замкнутого множества F. Обозначим через у₀ какую-либо предельную точку множества j (F) и найдем последовательность {у_n}, для которой

lim у_n = у₀ , у_n Î j(F).

Пусть х₀=j^-1(у₀), х_n= у ^–1(у_n).

Тогда х_nÎF. Но | х_n – х₀ | = | у_n – у₀ |, так что х_n ® х₀ и, в силу замкнутости F, х₀ Î F, откуда у₀ = j (х₀) Î j (F).

Значит j(F) есть открытое множество.

b) Пусть G есть открытое множество. Положим F=CG. Тогда F есть замкнутое множество и G+F=Z, G ·F=0.

Отсюда, в силу теоремы 2 и следствия теоремы 3,

j (G) + j (F) = Z,    j (G) j ·(F) = 0,

т.е. j (G) является дополнением замкнутого множества j (F) и, стало быть, открыто.

Теорема 6. Мера открытого ограниченного множества не меняется при движении.

Д о к а з а т е л ь с т в о. Пусть G открытое ограниченное множество. Тогда и j(G) есть открытое ограниченное множество. Обозначим через d_k(k = 1, 2, 3…) составляющие интервалы множества G. На основании теоремы 4, составляющими интервалами множества j(G) служат интервалы j(d_k), причем легко проверить, что этими интервалами исчерпываются все составляющие интервалы множества j(G). Отсюда: mj(G)= j(d_k)= d_k = mG, что и требовалось доказать.                                             

Теорема 7. Движение не изменяет ни внешней, ни внутренней меры ограниченного множества.

Д о к а з а т е л ь с т в о.а) Пусть E ограниченное множество. Взяв произвольное e>0, найдем такое открытое ограниченное множество G, чтобы было GÉE, mG < m* E + e.

В таком случае j(G) есть открытое ограниченное множество, содержащее множество j(E). Стало быть

m*j(E) £mj(G)=mG < m*E+e.

В силу произвольности числа e, следует, что m*j(E) £m* E, так что при движении внешняя мера ограниченного множества не увеличивается. Но тогда она и не уменьшается, ибо иначе обратное движение привело бы к увеличению внешней меры.

Итак

m*j(E)=m*E.

b) Обозначим через D  какой-нибудь интервал, содержащий множество Е. Тогда j (D) есть интервал, содержащий множество j (Е). Положим, далее, А=С_D E.

Соотношения Е+А=D, ЕА=0 дают, что

j (E)+j (А)= j ( D),  j (Е) · j (А)=0,

так что j (Е) есть дополнительные множества j (А) относительно интервала j (D).Отсюда, в силу теоремы 7,   

m* j (А)+m _*  j (Е)=mj (D)

и, на основании уже доказанной части теоремы и теоремы 4,

m* А+m_* j (Е)=mD.

Значит m_*j (Е)=mD-m* (C_DЕ), и снова применяя теорему 7, мы находим, что  

m_*j (Е)=m_* Е.

Следствие. При движении измеримое множество переходит в измеримое множество той же меры.

Определение 2. Множества А и В называются конгруэнтными, если существует движение, в котором одно из них переходит в другое.

С помощью этого термина доказанные результаты можно высказать в такой форме.

Теорема 8. Конгруэнтные множества имеют одинаковые внешнюю и внутреннюю меры. Множество, конгруэнтное измеримому множеству, измеримо и имеет ту же меру.