 |
Главная |
Соприкасающаяся плоскость кривой. Длина дуги кривой.
|
из
5.00
|
Спецглавы геометрии
Методические указания к практическим занятиям
и самостоятельной работе
для студентов направления подготовки 44.03.01
Курган 2017
Кафедра: «Фундаментальной математики и методики преподавания математики»
Дисциплины: «Спецглавы геометрии»
(направление 440301.62 «Математическое образование»)
Составили: канд. физ.-мат. наук О.Н. Хмеляр
Утверждены на заседании кафедры «19» октября 2017 г.
СОДЕРЖАНИЕ
Введение……………………………………………………………………………...4
Раздел 1 Дифференциальная геометрия..……………………………………….…5
Тема 1 Дифференциальная геометрия.…………………………………………….5
1 Геометрия кривых в евклидовом пространстве ………………………………...5
2 Геометрия поверхностей в евклидовом пространстве ..……………………….11
Список литературы.................................................................................................15
ВВЕДЕНИЕ
Настоящее пособие составлено в соответствии с программой дисциплины «Спецглавы геометрии» и предназначено для студентов направления Педагогическое образование «Математическое образование».
Здесь представлены все темы, которые выносятся на практические занятия и самостоятельную работу студентов. Для каждой темы указаны вопросы для повторения и задачи для решения. Также приведены основные теоретические положения и образцы решения типовых задач. По усмотрению преподавателя из раздела «Упражнения для решения» отбираются задачи для решения в аудитории и для самостоятельной работы студентов.
Раздел 1 Дифференциальная геометрия
Тема 1 Дифференциальная геометрия
Геометрия кривых в евклидовом пространстве
Вопросы теории
1. Вектор – функция скалярного аргумента.
2. Регулярные кривые.
3. Касательная к кривой.
4. Нормальная плоскость к линии.
5. Длина дуги. Натуральный параметр.
6. Кривизна кривой. Репер Френе.
7. Формулы Френе.
8. Кручение кривой.
9. Кривизна и кручение в произвольной параметризации.
Вектор-функция скалярного аргумента
Пусть  - множество точек на прямой, плоскости или в пространстве. Говорят, что на множестве
- множество точек на прямой, плоскости или в пространстве. Говорят, что на множестве  задана вектор-функция, если с каждой его точкой M сопоставлен вектор
задана вектор-функция, если с каждой его точкой M сопоставлен вектор  . Если
. Если  - множество точек
- множество точек  на прямой, то вектор-функция
на прямой, то вектор-функция 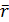 , заданная на U , является вектор-функцией одного скалярного аргумента:
, заданная на U , является вектор-функцией одного скалярного аргумента: 
Определение: Пределом вектор-функции  при
при  называется вектор
называется вектор  , для которого
, для которого 
Определение: Вектор-функция  называется непрерывной при
называется непрерывной при  , если
, если 
Определение: Производной вектор-функции  в точке
в точке  называется предел
называется предел  (если существует).
(если существует).
Задача: Доказать, что если  то
то 
Решение: По условию задачи  Отсюда и из неравенcтва
Отсюда и из неравенcтва  вытекает, что
вытекает, что 
Касательная к кривой
Если  векторное уравнение кривой
векторное уравнение кривой  , то уравнение касательной прямой в точке
, то уравнение касательной прямой в точке 


Если кривая задана уравнениями 

 то уравнение касательной прямой в точке
то уравнение касательной прямой в точке 

Если плоская кривая  задана уравнением
задана уравнением 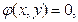 то уравнение касательной прямой в точке
то уравнение касательной прямой в точке 
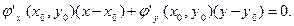
Задача: Составить уравнение касательной и нормали к линии  в точке
в точке 
Решение: Если плоская кривая задана уравнением  то уравнение касательной прямой в точке
то уравнение касательной прямой в точке  кривой имеет вид
кривой имеет вид 
Применительно к нашей задаче получим 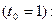




 и, тогда уравнение касательной примет вид
и, тогда уравнение касательной примет вид 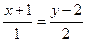 .
.
Направляющий вектор  нормали кривой в точке
нормали кривой в точке 
 перпендикулярен направляющему вектору
перпендикулярен направляющему вектору  касательной, поэтому можно положить
касательной, поэтому можно положить  Воспользовавшись уравнением прямой с заданным направляющим вектором и походящей через заданную точку, получим
Воспользовавшись уравнением прямой с заданным направляющим вектором и походящей через заданную точку, получим  - уравнение нормали кривой в точке
- уравнение нормали кривой в точке 
Ответ: 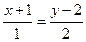 ,
,  .
.
Соприкасающаяся плоскость кривой. Длина дуги кривой.
Если кривая  задана уравнением
задана уравнением  или уравнениями
или уравнениями 

 то уравнение соприкасающейся плоскости в точке
то уравнение соприкасающейся плоскости в точке  имеет вид:
имеет вид:
 или
или  (1)
(1)
Определение: Главная нормаль кривой – нормаль кривой, лежащая в соприкасающейся плоскости. Бинормаль кривой - нормаль кривой, перпендикулярная соприкасающейся плоскости.
Если кривая  задана уравнением
задана уравнением  или параметрическими уравнениями
или параметрическими уравнениями 


 , то длина дуги кривой
, то длина дуги кривой  определяется
определяется 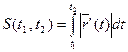 или
или 
Задача: Найти длину дуги винтовой линии 
 от точки пересечения с плоскостью
от точки пересечения с плоскостью  до произвольной точки
до произвольной точки  .
.
Решение: Точка 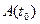 пересечения винтовой линии с плоскостью
пересечения винтовой линии с плоскостью  определяется из ее уравнения при
определяется из ее уравнения при  то есть
то есть  Поэтому находим длину дуги линии
Поэтому находим длину дуги линии 

Ответ: 
Задача: Составить уравнение соприкасающейся плоскости, бинормали и главной нормали линии  в точке
в точке 
Решение: Пусть  - уравнение линии в векторной форме, тогда
- уравнение линии в векторной форме, тогда 


 отсюда
отсюда 


Тогда уравнение (1) соприкасающейся плоскости примет вид: 
Упрощая, получим искомое уравнение 
Вектор нормали соприкасающейся плоскости 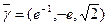 является направляющим вектором бинормали. Из условия прохождения бинормали через точку
является направляющим вектором бинормали. Из условия прохождения бинормали через точку  получим уравнение бинормали:
получим уравнение бинормали:  Из определения главной нормали вытекает, что ее направляющий вектор
Из определения главной нормали вытекает, что ее направляющий вектор  ортогонален направляющим векторам бинормали
ортогонален направляющим векторам бинормали 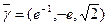 и касательной
и касательной  Поэтому можно положить, что
Поэтому можно положить, что 
Уравнение главной нормали примет вид: 
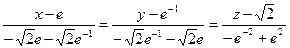 или
или  .
.
Ответ: 
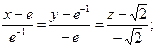

|
из
5.00
|
Обсуждение в статье: Соприкасающаяся плоскость кривой. Длина дуги кривой. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

