Проведение касательной к окружности

 

 

Задана окружность с центром О и точка А, лежащая вне окружности (рис.9). Требуется провести из точки А касательную к окружности.

 

 

Рис. 9

1. Точку А соединяют прямой с заданным центром О окружности.

Строят вспомогательную окружность диаметром, равным ОА. Чтобы найти центр О₁ , делят отрезок ОА пополам (рис.9).

2. Точки К и К₁ пересечения вспомогательной окружности с заданной – точки касания.

3. Точку А соединяют с точками касания.

 

Построение общей касательной к двум окружностям

 

 

Заданы две окружности радиусом R и R_{1 .} Требуется построить касательную к ним.

Различают два случая касания: внешнее и внутреннее.

Внешнее касание.

 

Рис. 10

 

1. Из центра О проводят вспомогательную окружность радиусом R - R₁.

2. На прямой ОО₁ из средней точки, через центр О₁ строят вторую вспомогательную окружность.

3. Точка пересечения этих окружностей В определяет направление радиуса ОК, идущего в точку касания К.

4. Для получения точки касания на второй окружности проводят из центра О₁ радиус  О₁К₁ïï ОК.

5. Найденные точки касания соединяют прямой линией.

Внутреннее касание

 

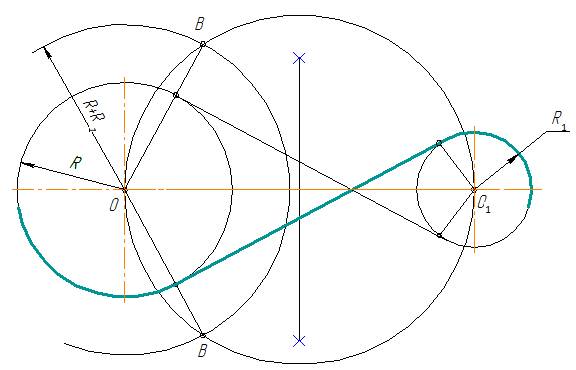
Рис. 11

При внутреннем касании  построение проводят аналогично, что и при внешнем, но из центра большой окружности проводят вспомогательную окружность радиусом, равным сумме радиусов данных окружностей, т.е. R + R₁ (рис.11) 

 

Сопряжение двух пересекающихся прямых

 

 

Даны пересекающиеся  под прямым, острым и тупым углами прямые линии.

Требуется построить сопряжения этих прямых дугой заданного радиуса R.

Рис. 12

1. Для нахождения центра сопряжения проводят вспомогательные прямые, параллельные данным на расстоянии равном радиусу R. Точка пересечения этих прямых т.О и будет центом  дуги сопряжения (рис.12)

2. Перпендикуляры, опущенные из центра дуги сопряжения т.О на данные прямые, определяют точки касания К и N.

3. Из точки О, как центра, описывают дугу заданного радиуса R.

Рис. 13

Примечание. Для прямых углов центр сопряжения удобнее находить с помощью циркуля (рис.13).

 

 

Сопряжение дуги окружности и прямой линии дугой заданного радиуса.

Внешнее касание

 

 

Дана окружность радиуса R и прямая АВ. Требуется соединить их дугой радиусом R1.

 

 

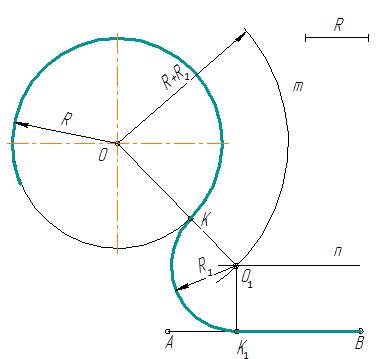
 (Рис. 14)

1. Для нахождения центра сопряжения из центра О заданной окружности проводят дугу m  радиуса R + R₁ и на расстоянии R₁ – прямую n // AB. Точка  О₁  пересечения прямой nи дуги m будет центром сопряжения.

2. Для получения точек сопряжения: К и К₁  проводят линию центров ОО₁ и восстанавливают к прямой АВ перпендикуляр ОК₁.

3. Из центра сопряжения О₁ между точками К и К₁  проводят дугу сопряжения радиусом R₁.

Внутреннее касание

 

 

В случае внутреннего касания выполняют те же построения, но дугу m вспомогательной окружности проводят радиусом R - R1.

 

Рис. 15