 |
Главная |
Интегральная функция распределения результатов экспериментальных исследований
|
из
5.00
|
Лабораторная работа № 1
Риски оценивается при помощи тех или иных показателей. Показатели ущерба могут быть количественными или качественными. Количественныепоказатели:количество и тяжесть профессиональных заболеваний, продолжительность временной утраты трудоспособности, сумма пособий по временной нетрудоспособности, количество случаев стойкой утраты профессиональной трудоспособности, степень утраты профессиональной трудоспособности в процентах, сумма расходов на обеспечение по страхованию по данному виду экономической деятельности и другие показатели. Качественные показатели: Ущерб от несчастных случаев классифицируют по их тяжести, например:легкий ущерб, когда пострадавшему работнику не требуется оказания медицинской помощи; в худшем случае 3-дневное отсутствие на работе, средний ущерб, когда пострадавшего работника доставляют в организацию здравоохранения или требуется ее посещение; отсутствие на работе до 30 дней; развивается хроническое заболевание, тяжелый ущерб, когда несчастный случай вызывает серьезное (неизлечимое) повреждение здоровья, требуется лечение в стационаре; отсутствие на работе более 30 дней; стойкая утрата трудоспособности или смерть.Допускается использовать и другие качественные показатели ущерба здоровью - несущественный, малый, средний, существенный, большой, несовместимый с жизнью и т.д
Если оценка риска оценивается по индексу травматизма (количество дней временной утраты трудоспособности в результате несчастных случаев на 1000 работников за один год), то в каждой единице продукции количественный признак качества принимает некоторое случайное значение, т.е. является случайной величиной и имеет некоторое распределение.
Интегральная функция распределения случайной величины F ( x) – это функция, показывающая зависимость вероятности того, что случайная величина X не превышает некоторый уровень x:
p ( X < x ) = F ( x )
Вероятность попадания случайной величины в некоторый интервал равна разности значений интегральных функций распределения в концах этого интервала:
p ( x 1 < X < x 2 ) = F ( x 2 ) – F ( x 1 )
Дифференциальная (или весовая) функция (или плотность) распределения f(x) случайной величины является производной от интегральной функции. Она приближённо равна отношению вероятности попадания случайной величины внутрь некоторого интервала к длине этого интервала. Вероятность попадания случайной величины в некоторый интервал равна площади под кривой дифференциальной функции распределения в этом интервале. Площадь под всей кривой дифференциальной функции равна единице.
Наиболее часто количественный показатель качества имеет приблизительно нормальное распределение. Любое нормальное распределение имеет два параметра, однозначно определяющих его: математическое ожидание показателя m и среднее квадратичное отклонение s (или дисперсия s2) как мера рассеяния показателя.
Пример 1.1.За 2014 год были выбраны 30 случайных городов России. Индекс травматизма представлен в следующем ряду: 9,2 12,2 10,5 9,4 8,9 7,4 10,1 11,7 11,4 11,0 10,2 8,0 7,3 7,0 9,6 8,4 10,8 8,4 11,2 8,8 10,7 8,6 9,7 9,8 9,5 12,5 9,8 9,5 9,2 7,7. Известно, что распределение показателя индекса травматизма приблизительно соответствует нормальному. Необходимо найти параметры распределения и построить графики интегральной и дифференциальной функций распределения ёмкости пластин.
Используем программу Excel пакета MS Office. Открываем новую книгу программы и переименовываем Лист 1 в Задание 1. Для этого можно на ярлыке с названием листа открыть контекстное меню (правой кнопкой мыши) и выбрать команду. Переименовать. На этом листе будем проводить все вычисления и построения.
В ячейку А1 вводим заголовок работы Лаб. работа 1. Распределение показателей качества по количественному признаку.. В ячейку А5 вводим заголовок столбца Индекс травматизма. Далее, начиная с ячейки А6 в столбец А вводим значения ёмкости пластин.
Затем находим параметры распределения. Вообще говоря, параметры распределения не могут быть найдены абсолютно точно никогда. Однако при объёме выборки не менее 30 обычно считают, что точечные оценки параметров нормального распределения с приемлемой точностью равны параметрам. Оценкой математического ожидания mявляется среднее значение выборки  , а оценкой среднего квадратичного отклонения (СКО) s – выборочное СКО s.
, а оценкой среднего квадратичного отклонения (СКО) s – выборочное СКО s.
Таким образом, расчёт параметров распределения может быть выполнен следующим образом: в ячейку А3 вводим текст m = и выравниваем его по правому краю ячейки кнопкой на панели инструментов. В соседней ячейке В3 рассчитываем значение среднего выборки как оценку математического ожидания. Для этого выбираем команду Вставка 4 Функция (или нажимаем соответствующую кнопку на панели инструментов) и в диалоговом окне выбираем статистическую функцию СРЗНАЧ. В окно Число 1 вводим диапазон ячеек с данными А6:А35 путём выделения этого диапазона указателем мыши при нажатой левой кнопке. (Внимание! Адреса ячеек вводить в формулы рекомендуется путём указания мышью на эти ячейки., но не вводом адресов с клавиатуры, который значительно увеличивает вероятность ошибок и замедляет работу). Нажав кнопку ОК, получаем в ячейке В3 значение математического ожидания 9,61667. В ячейку D3 вводим текст s = и выравниваем его по правому краю. В соседней ячейке F3 рассчитываем выборочное СКО как оценку генерального СКО по статистической функции СТАНДОТКЛОН. Получаем значение СКО 1,437691.
Для построения графиков нужны столбцы данных x, F ( x ) и f( x ). Соответствующие заголовки вводим в ячейках С5, D5, E5.
В столбце с заголовком xдолжны находиться значения квантиля распределения (в данном случае – ёмкости). Целесообразно варьировать x в интервале m ± 3 s , поскольку в соответствии с правилом трёх сигм в этом интервале находится практически 100% значений случайной величины (более точно – 99,73%). Поэтому в ячейку С6 вводим значение 5,4, что примерно равно m - 3 s . Затем вводим остальные значения х командойПравка 4 Заполнить 4 Прогрессия. В открывшемся диалоговом окне выбираем расположение по столбцам, шаг 0,1 (чтобы получить достаточно много точек для построения графиков) и предельное значение 13,8, соответствующее примерно m + 3 s. В результате выполнения команды столбец будет заполнен значениями, возрастающими с шагом 0,1 до значения 13,8 в ячейке С90.
Далее в ячейке D6 рассчитываем значение интегральной функции распределения F ( x) для квантиля 5,4 по статистической функции НОРМРАСП. В открывшемся диалоговом окне делаем ссылки на соответствующие ячейки, в строке Интегральный вводим (в соответствии со справкой в нижней части окна) значение истина и получаем в ячейке D6 значение 0,001679. Аналогичным образом в ячейке E6 рассчитываем значение дифференциальной функции распределения f ( x ) для квантиля 5,4, но в строке Интегральный вводим (в соответствии со справкой в нижней части окна) значение ложь. Получаем значение f ( x ), равное 0,003761.
Формулы из ячеек D6 иE6 следует скопировать в диапазон D7:E90. Однако сначала надо задать в формулах абсолютную адресацию для тех строк, столбцов или ячеек, адреса которых при копировании не должны меняться. В обеих формулах абсолютные адреса должны быть у ячеек B3 и E3, в которых содержатся значения математического ожидания и СКО. В адресах этих ячеек перед именами строк и столбцов следует ввести символ $. Это можно сделать в строке формул вводом с клавиатуры, но более эффективен следующий способ: в строке формул выделить адреса нужных ячеек указателем мыши, нажать клавишу F4, а затем Enter. В результате, например, в ячейке D6 должна быть получена формула =НОРМРАСП(C6;$B$3;$E$3;ИСТИНА).
После этого можно скопировать формулы из ячеек D6 и E6 в диапазон D7:E90. На этом расчёт данных для построения графиков будет закончен (рис. 1.1).
Для построения графика интегральной функции распределения открываем Мастер диаграмм, выбираем тип диаграммы Точечная и видСо значениями, соединёнными сглаживающими линиями без маркеров. На втором шаге выделяем диапазон С6:D90, На третьем шаге вводим заголовки (заголовки см. на рис.1.2) и основные линии сетки, отменяем легенду. На четвёртом шаге помещаем диаграмму на имеющемся листе. Полученную (после нажатия кнопки Готово) диаграмму редактируем, используя контекстное меню и двойной щелчок мышью на редактируемых элементах диаграммы. Полученный график интегральной функции распределения показан на рис. 1.2.

Рис.1.1. Результаты расчёта параметров распределения и данных
для построения графиковв примере 1.1

Рис. 1.2. Интегральная функция распределения индекса травматизма
Для построения графика дифференциальной функции распределения выполняем аналогичные действия. При этом на втором шаге в качестве диапазона данных выделяем диапазоны ячеек С6:С90 и Е6:Е90. Поскольку эти диапазоны находятся не в соседних столбцах, их выделение может быть сделано при нажатой клавише Ctrl. График дифференциальной функции распределения показан на рис. 1.3.
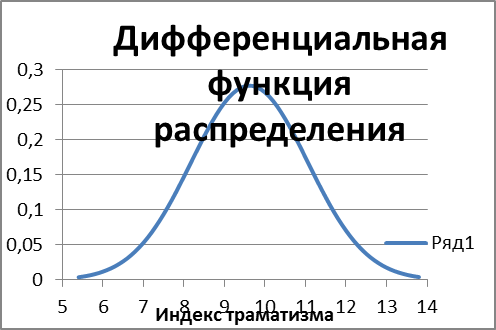
Рис. 1.3. Дифференциальная функция распределения индекса травматизма
Задание.
1. Выполнить расчёты и построения в соответствии с примером 1.1. Чему равна вероятность того, что индекс травматизма случайно выбранного города меньше 11? Чему равна вероятность того, что индекс травматизма случайно выбранного города находится в интервале от 9 до 10?
2. Построить на одной диаграмме графики интегральных функций трёх нормальных распределений, имеющих параметры, приведённые в табл. 1.1.
3. Построить на одной диаграмме графики дифференциальных функций трёх нормальных распределений, имеющих параметры, приведённые в табл. 1.1.
4. Сделать выводы о влиянии параметров распределения на вид и положение графиков функций распределения.
Таблица 1.1.
| № | Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 | Вариант 5 | |||||
| m | s | m | s | m | s | m | s | m | s | |
| 1 | 1 | 2 | 2 | 2 | 6 | 1 | 0,5 | 0,5 | 1 | 4 |
| 2 | 2 | 2 | 2 | 4 | 9 | 1 | 1 | 0,5 | 0,5 | 4 |
| 3 | 2 | 4 | 1 | 4 | 9 | 3 | 1 | 2 | 0,5 | 2 |
| № | Вариант 6 | Вариант 7 | Вариант 8 | Вариант 9 | Вариант10 | |||||
| m | s | m | s | m | s | m | s | m | s | |
| 1 | 2 | 3 | 0,5 | 0,5 | 3 | 3 | 5 | 2 | 40 | 30 |
| 2 | 0 | 3 | 0,5 | 1 | 1 | 3 | 3 | 2 | 50 | 30 |
| 3 | 0 | 1 | 1 | 1 | 1 | 1 | 3 | 1 | 50 | 20 |
| № | Вариант 11 | Вариант 12 | Вариант 13 | Вариант 14 | Вариант15 | |||||
| m | s | m | s | m | m | s | m | s | ||
| 1 | 0 | 2 | 1 | 0,5 | 1 | 2 | 2 | 4 | 0 | 0,5 |
| 2 | 1 | 2 | 0,5 | 1 | 3 | 4 | 1 | 3 | 0,5 | 1 |
| 3 | 1 | 1 | 1 | 0,5 | 1 | 3 | 0 | 1 | 1 | 1 |
| № | Вариант 16 | Вариант 17 | Вариант 18 | Вариант 19 | Вариант20 | |||||
| m | s | m | s | m | s | m | s | m | s | |
| 1 | 1 | 3 | 50 | 20 | 0 | 2 | 0 | 4 | 0 | 0,5 |
| 2 | 1 | 2 | 40 | 30 | 1 | 2 | 2 | 2 | 0,5 | 1 |
| 3 | 1 | 4 | 40 | 30 | 0 | 0 | 1 | 3 | 1 | 0 |
|
из
5.00
|
Обсуждение в статье: Интегральная функция распределения результатов экспериментальных исследований |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

