Косвенный метод наименьших квадратов.

Рассмотрим случай двух уравнений с двумя эндогенными переменными:

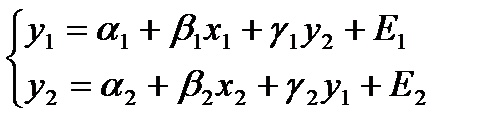(1)

Данная система разрешима обычным МНК.

В основе косвенного метода наименьших квадратов (КМНК) лежит простая идея. Поскольку препятствием к применению МНК является коррелированность эндогенных переменных со случайными членами, следует разрешить СОУ относительно эндогенных переменных Y так, чтобы в правых частях остались лишь экзогенные переменные Х. Для уравнений вида (1) это всегда можно сделать. Затем применить обычный МНК к полученным уравнениям и получить оценки выражений от исходных параметров, из которых потом найти оценки и самих параметров. Такая процедура называется КМНК.

Применим процедуру КМНК к системе (1),т.к.

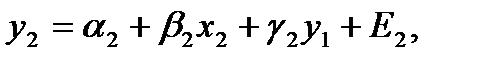
то

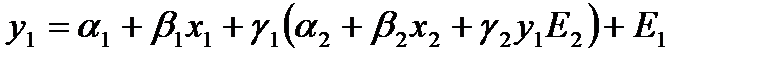
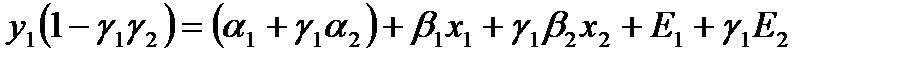
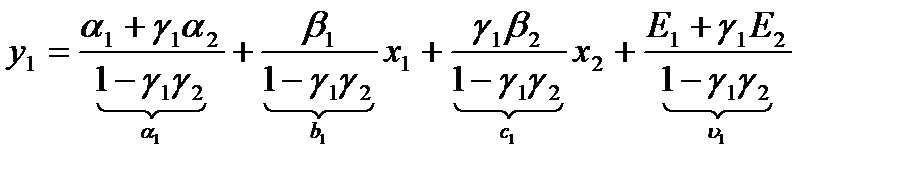
или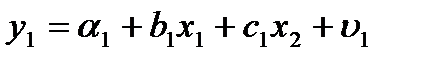

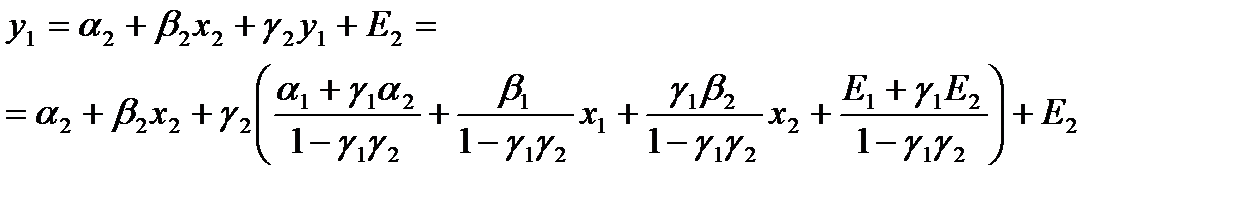    Аналогичными преобразованиями получим, что

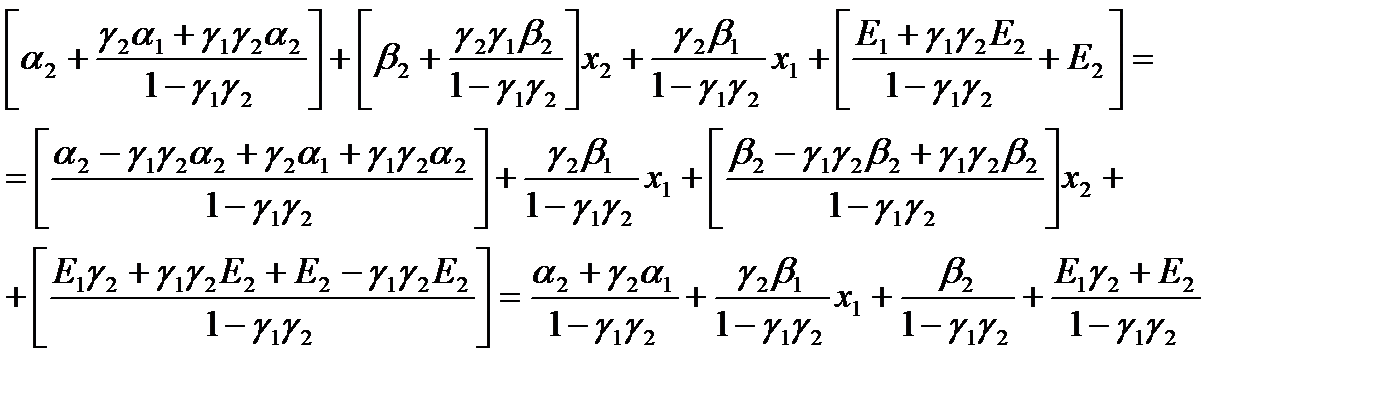
и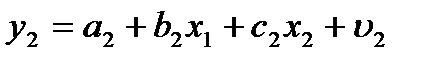

Получим систему одновременных уравнений:

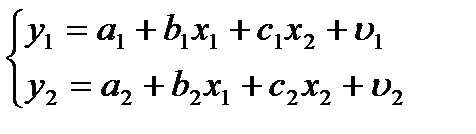                             (2)

Равенства

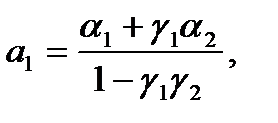
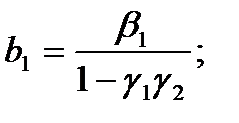
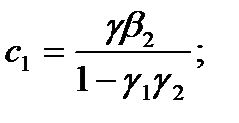
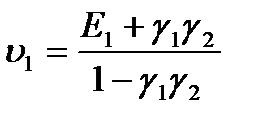      (3)

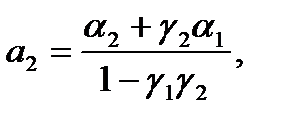
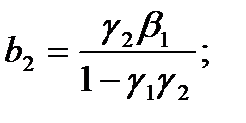
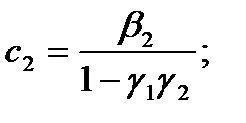
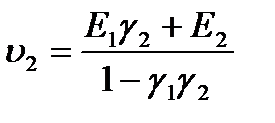
позволяют однозначно выразить исходные параметры 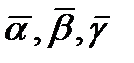через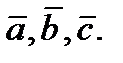

Форма (2) называется приведенной формой системы. Параметры приведенной формы оцениваются с помощью метода наименьших квадратов.

Применение косвенного метода наименьших квадратов

Непосредственное применение метода наименьших квадратов (МНК) для каждого из уравнений системы одновременных уравнений в структурной форме, как правило, приводит к получению смещенных и несостоятельных оценок. Обычно это происходит вследствие коррелированности одной или нескольких объясняющих переменных со случайным отклонением.

Для получения «хороших» оценок параметров модели необходимо использовать другие методы. Одним из таких возможных методов является косвенный метод наименьших квадратов (КМНК), основанный на использовании приведенной формы модели.

КМНК включает следующие этапы:

1) исходя из структурной формы модели, строится ее приведенная форма;

2) по МНК оцениваются параметры уравнений в приведенной форме;

3) на основе оценок параметров, найденных на этапе 2, оцениваются параметры структурных уравнений (если это возможно).

Пример 1. Рассмотрим модификацию модели «спрос–предложение» в виде следующей системы регрессионных уравнений:

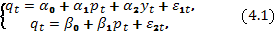
Где 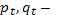 эндогенные переменные: цена и количество товара в году t, 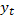– экзогенная переменная: доход потребителей; 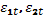– случайные отклонения.

Требуется оценить параметры этой модели по пяти наблюдениям переменных 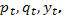 представленным в нижеследующей таблице 1.

Таб. 1.

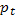
	1	2	3	4	5
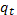
	8	10	7	5	1
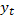
	2	4	3	5	2

Преобразуем данную систему в приведенную форму. Для этого вычтем из функции спроса функцию предложения. Получим:

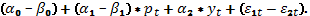
Отсюда последовательно находим выражения для 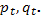Таким образом, приведенная форма исходной модели имеет вид:

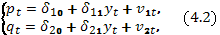
где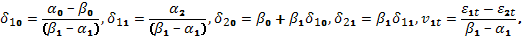

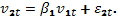
По имеющимся статистическим данным оценим коэффициенты приведенных уравнений (4.2), применяя формулы для МНК-оценок параметров парной регрессии:

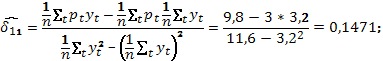
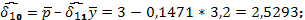
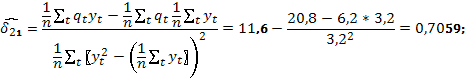
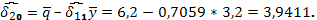
По полученным оценкам не трудно восстановить оценки параметров функции предложения (второго уравнения системы (4.1)). Действительно, из уравнений 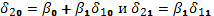 выразим  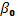и :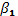

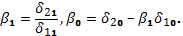
Следовательно,

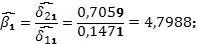
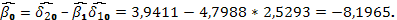
И функция предложения имеет вид:

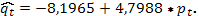
В то же время рассчитанные непосредственно по МНК оценки параметров данного уравнения будут:

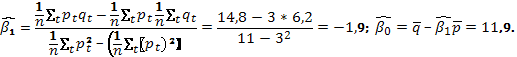
Тогда функция предложения имеет вид, совсем отличный от выражения, рассчитанного с помощью косвенного МНК: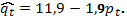

Таким образом, непосредственное применение МНК в несоответствующих ситуациях может существенно исказить картину зависимости.

Существует и другой способ реализации косвенного МНК, несвязанный с теоретическим преобразованием структурной формы в приведенную форму, как это, например, было сделано выше при переходе от системы (4.1) к системе (4.2).

На первом этапе КМНК достаточно лишь обозначить вид приведенной формы, не выражая ее параметры через параметры структурной формы. Далее, как и выше, с помощью обычного МНК оцениваются параметры приведенной формы.

На третьем этапе с помощью простейших алгебраических операций полученные уравнения приведенной формы преобразуются в оцененные уравнения структурной формы.