Правило сложения и вычитания комплексных чисел.

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА

Филиал федерального государственного бюджетного образовательного учреждения высшего образования

«Самарский государственный университет путей сообщения» в г. Саратове

Филиал СамГУПС в г. Саратове

Методические рекомендации по выполнению практических работ

По математике

Студента группы

 

Саратов

2019-2020 учебный год

Перечень практических работ

Практическая работа № 1 Алгебраическая форма записи комплексных чисел. Действия над комплексными числами, заданными в алгебраической форме. Геометрическая интерпретация комплексных чисел. Показательная и тригонометрическая формы записи комплексных чисел. Действия над комплексными числами, заданными в тригонометрической и показательной формах.

       Практическая работа № 2 Решение профессиональных задач методом комплексных чисел.

Практическая работа № 3 Определение максимума мощности в цепи постоянного тока с применением производной

Практическая работа №4Вычисление площадей и объемов при проектирования объектов транспорта с применением определенного»

Практическая работа №5 Вычисление интегралов по методам прямоугольников, трапеций, Симпсона.

 Практическая работа № 6 Решение задач на нахождение по таблично заданной функции (при n =2), функции заданной аналитически. Исследование свойств функции для определения эффективности планирования технического цикла объектов связи на железнодорожном транспорте.

Практическая работа № 7 Решение дифференциальных уравнений методом Эйлера.Использование дифференциальных уравнений в расчетах эффективности профессиональной деятельности

Практическая работа № 8 Разложение функций в ряд Маклорена.

Практическая работа № 9 Расчет электрических цепей несинусоидальных периодических токов с применение рядов Фурье.

Практическая работа № 10 Оценка результатов тестового эксперимента эффективности работы механизмов и оборудования на железнодорожном транспорте по средствам определения сходимости числового ряда по признаку Даламбера.

Практическая работа № 11  Построение графа в структуре взаимодействия различных видов транспорта, формировании технологического цикла оказания услуг на транспорте.

Практическая работа № 12 Решение задач на нахождение вероятности события при изучении и планировании рынка услуг на транспорте»

Практическая работа № 13 Решение задач с применением теорем сложения и умножения вероятностей.

Практическая работа № 14 Построение закона распределения случайной величины (по заданным условиям).

Практическая работа № 15 Расчёт математических характеристик дискретной случайной величины.

                     

Практическая работа № 1

Тема: « Алгебраическая форма записи комплексных чисел. Действия над комплексными числами, заданными в алгебраической форме. Геометрическая интерпретация комплексных чисел Показательная и тригонометрическая формы записи комплексных чисел. Действия над комплексными числами, заданными в тригонометрической и показательной формах».

                            Теоретический материал

Существует элемент i (мнимая единица) такой, что i² = – 1. Символ a + bi называют комплексным числом с действительной частью a и мнимой частью bi, где a и b – действительные числа, b – коэффициент мнимой части. Комплексное число a + 0i отождествляется с действительным числом a, т.е. a + 0i = a, в частности, 0 + 0i = 0. Числа вида bi (b 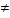0) называют чисто мнимыми.

Например, комплексное число 2 + 3i имеет действительную часть – действительное число 2 и мнимую часть 3i, действительное число 3 – коэффициент мнимой части. Комплексное число 2– 3i имеет действительную часть число 2, мнимую часть – 3i, число – 3– коэффициент при мнимой части.

Правило равенства. Два комплексных числа равны тогда и только тогда, когда равны их действительные части и равны коэффициенты мнимых частей, т.е., если a + bi = c +di, то a = c, b = d: и, обратно, если a = c, b = d, то a + bi = c +di.

Правило сложения и вычитания комплексных чисел.

(a + bi) + (c + di) = (a + c) + (b + d)i.

Например: (2 + 3i) + (5 + i) = (2 + 5) + (3 + 1)i = 7 + 4i;

              (– 2 + 3i) + (1 – 8i) = (– 2 + 1) + (3 + (– 8))i = – 1 – 5i;

              (– 2 + 3i) + (1 – 3i) = (– 2 + 1) + (3 + (– 3))i = – 1 + 0i = – 1.

Вычитание комплексных чисел определяется как операция, обратная сложению, и выполняется по формуле: ( a + bi ) – ( c + di ) = ( a – c ) + ( b – d ) i .

Например:

(5 – 8i) – (2 + 3i) = (3 – 2) + (– 8 – 3)i = 1 – 11i; (3 – 2i) – (1 – 2i) = (3 – 1) + ((– 2) – (– 2))i = 2 + 0i = 2.

Правило умножения комплексных чисел. ( a + bi )( c + di ) = ( a с + bd ) + ( ad + bc ) i

Деление комплексного числа a + bi на комплексное число c + di 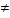0

.

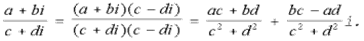Для комплексных чисел существует три формы записи: алгебраическая форма записи, тригонометрическая форма записи и экспоненциальная (показательная) форма записи. Алгебраическая форма - это такая форма записи комплексных чисел, при которой комплексное число z, заданное парой вещественных чисел (x , y), записывается в виде z =x+iy. (1), где символ i, называется мнимой единицей. Число x вещественной (реальной) частью комплексного числа z=x+iy и обозначают Rez. Число y называют мнимой частью комплексного числа z =x +i y и обозначают Imz. Комплексные числа, у которых Imz = 0 , являются вещественными числами. Комплексные числа, у которых Rez = 0 , являются чисто мнимыми числами. Модулем комплексного числа z = x + i y называют вещественное число, обозначаемое |z| и определенное по формуле 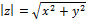 Изображение комплексных чисел радиус-векторами координатной плоскости Рассмотрим плоскость с заданной прямоугольной декартовой системой координат xOу . Назовем рассматриваемую плоскость комплексной плоскостью, и представим комплексное число z = x + i y радиус–вектором с координатами (x , y).

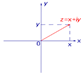 рис 1.

Назовем ось абсцисс Ox вещественной осью, а ось ординат Oy- мнимой осью. При таком представлении комплексных чисел сумме комплексных чисел соответствует сумма радиус-векторов, а произведению комплексного числа на вещественное число соответствует произведение радиус–вектора на это число.

Аргумент комплексного числа Рассмотрим радиус–вектор произвольного, но отличного от нуля, комплексного числа z. Аргументом комплексного числаz называют угол φ между положительным направлением вещественной оси и радиус-вектором z. Аргумент комплексного числа z считают положительным, если поворот от положительного направления вещественной оси к радиус-вектору z происходит против часовой стрелки, и отрицательным- в случае поворота по часовой стрелке

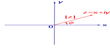 Рис.2

Комплексное число нуль аргумента не имеет. Поскольку аргумент любого комплексного числа определяется с точностью до слагаемого 2kπ , где k - произвольное целое число, то вводится, главное значение аргумента, обозначаемое arg z и удовлетворяющее неравенствам:

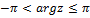Тогда оказывается справедливым равенство:  Если для комплексного числа z=x iy известны его модуль r=|z| и аргумент φ, то можем найти вещественную и мнимую части по формулам

(3)