 |
Главная |
Тема «Решение дифференциальных уравнений методом Эйлера. Использование дифференциальных уравнений в расчетах эффективности профессиональной деятельности»
|
из
5.00
|
Дифференциальные уравнения – это уравнения, содержащие производные некоторой функции 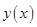 . В дальнейшем вместо слов дифференциальное уравнение будем писать ДУ.
. В дальнейшем вместо слов дифференциальное уравнение будем писать ДУ.
Если ДУ содержит обычные производные функции одной переменной, то оно называется обыкновенным дифференциальным уравнением.
Если уравнение содержит частные производные функции нескольких переменных, то оно называется ДУ в частных производных. Рассмотрим обыкновенные дифференциальные уравнения. Исходя из этого определения, в качестве примеров, рассмотрим три простых дифференциальных уравнения:
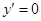 , ,
| (1) | |||
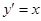 , ,
| (2) | |||
|
| (3) | |||
ДУ может содержать также производные различных порядков, выше первого: 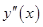 , . . . ,
, . . . , 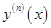 . Например, уравнение
. Например, уравнение
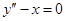
| (4) |
содержит производную второго порядка 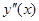 , а уравнение
, а уравнение
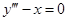
| (5) |
содержит производную третьего порядка 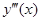 . Самый высокий порядок производной, входящей в уравнение, называется порядком дифференциального уравнения. Поэтому уравнения (1), (2) и (3) это ДУ первого порядка, а уравнения (4) и (5) это ДУ второго и третьего порядков соответственно.
. Самый высокий порядок производной, входящей в уравнение, называется порядком дифференциального уравнения. Поэтому уравнения (1), (2) и (3) это ДУ первого порядка, а уравнения (4) и (5) это ДУ второго и третьего порядков соответственно.
Решением ДУ называется функция 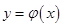 , которая обращает это уравнение в тождество. График решения на плоскости
, которая обращает это уравнение в тождество. График решения на плоскости 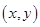 называется интегральной кривой. Например, решением уравнения
называется интегральной кривой. Например, решением уравнения 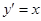 (2) является функция
(2) является функция 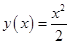 (6), график которой (интегральная кривая)представляет собой параболу. Если к правой части равенства (6) прибавить любое число (например,
(6), график которой (интегральная кривая)представляет собой параболу. Если к правой части равенства (6) прибавить любое число (например, 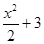 ), то функция также будет решением уравнения (2).
), то функция также будет решением уравнения (2).
В этом случае решение определяется с точностью до произвольной постоянной.
Множество решений 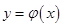 +С, где С - произвольная постоянная, называется общим решением ДУ.
+С, где С - произвольная постоянная, называется общим решением ДУ.
Например, общее решение уравнения (2) имеет вид
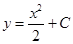 . .
| (7) |
Это решение, содержащее одну произвольную постоянную, является общим решение ДУ первого порядка (2). Очевидно, что решением уравнения 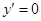 (1) является любая постоянная. Таким образом, общее решение уравнения (1) можно записать в виде
(1) является любая постоянная. Таким образом, общее решение уравнения (1) можно записать в виде
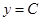 . .
| (8) |
Подставляя конкретные значения постоянной 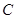 , будем получать решения уравнения, которые называются частными решениями. Используя понятие производной второго порядка, перепишем уравнение
, будем получать решения уравнения, которые называются частными решениями. Используя понятие производной второго порядка, перепишем уравнение 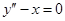 (4) в виде
(4) в виде 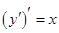 (9)Тогда аналогично уравнению (2), получим
(9)Тогда аналогично уравнению (2), получим 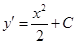 (10) И далее
(10) И далее 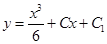 (11)
(11)
Это общее решение уравнения второго порядка (4), содержит две произвольные постоянные.
Аналогично можно найти общее решение ДУ третьего порядка 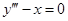 (5):
(5):
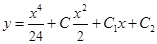 (12) Оно содержит три произвольные постоянные.
(12) Оно содержит три произвольные постоянные.
Решить уравнение 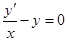 (3) сложнее. Для этого нужно использовать один из методов решения ДУ первого порядка.
(3) сложнее. Для этого нужно использовать один из методов решения ДУ первого порядка.
Практическая работа № 8
Тема «Разложение функций в ряд Маклорена»
|
из
5.00
|
Обсуждение в статье: Тема «Решение дифференциальных уравнений методом Эйлера. Использование дифференциальных уравнений в расчетах эффективности профессиональной деятельности» |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

