 |
Главная |
Практическая работа№ 7
|
из
5.00
|
«Оценка результатов тестового эксперимента эффективности работы механизмов и оборудования на железнодорожном транспорте по средствам, определения сходимости числового ряда по признаку Даламбера».
Краткие теоретические сведения:
Перед тем как сформулировать сам признак, рассмотрим важный вопрос:
Когда нужно применять признак сходимости Даламбера?
Сначала начнем с повторения. Вспомним случаи, когда нужно применять самый ходовойпредельный признак сравнения. Предельный признак сравнения применяется тогда, когда в общем члене ряда:
1) В знаменателе находится многочлен.
2) Многочлены находятся и в числителе и в знаменателе.
3) Один или оба многочлена могут быть под корнем.
Основные же предпосылки для применения признака Даламбера следующие:
1) В общий член ряда («начинку» ряда) входит какое-нибудь число в степени, например, 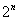 ,
, 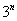 ,
,  и так далее. Причем, совершенно не важно, где эта штуковина располагается, в числителе или в знаменателе – важно, что она там присутствует.
и так далее. Причем, совершенно не важно, где эта штуковина располагается, в числителе или в знаменателе – важно, что она там присутствует.
2) В общий член ряда входит факториал. С факториалами мы познакомились ещё на уроке «Числовая последовательность и её предел». 




…


…Признак Даламбера: Рассмотрим положительный числовой ряд  . Если существует предел отношения последующего члена к предыдущему:
. Если существует предел отношения последующего члена к предыдущему:  , то:
, то:
а) При  ряд сходится. В частности, ряд сходится при
ряд сходится. В частности, ряд сходится при  .
.
б) При  ряд расходится. В частности, ряд расходится при
ряд расходится. В частности, ряд расходится при  .
.
в) При  признак не дает ответа. Нужно использовать другой признак. Чаще всего единица получается в том случае, когда признак Даламбера пытаются применить там, где нужно использовать предельный признак сравнения.
признак не дает ответа. Нужно использовать другой признак. Чаще всего единица получается в том случае, когда признак Даламбера пытаются применить там, где нужно использовать предельный признак сравнения.
Пример 1
Исследовать ряд на сходимость 
Мы видим, что в общем члене ряда у нас есть  , а это верная предпосылка того, что нужно использовать признак Даламбера. Сначала полное решение и образец оформления, комментарии ниже.
, а это верная предпосылка того, что нужно использовать признак Даламбера. Сначала полное решение и образец оформления, комментарии ниже.
Используем признак Даламбера:

Таким образом, исследуемый ряд сходится.
(1) Составляем отношение следующего члена ряда к предыдущему: 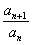 . Из условия мы видим, что общий член ряда
. Из условия мы видим, что общий член ряда  . Для того, чтобы получить следующий член ряда необходимо вместо
. Для того, чтобы получить следующий член ряда необходимо вместо  подставить
подставить  :
:  .
.
(2) Избавляемся от четырехэтажности дроби. При определенном опыте решения этот шаг можно пропускать.
(3) В числителе раскрываем скобки. В знаменателе выносим четверку из степени.(4) Сокращаем на  . Константу
. Константу  выносим за знак предела. В числителе, в скобках,приводим подобные слагаемые.
выносим за знак предела. В числителе, в скобках,приводим подобные слагаемые.
(5) Неопределенность  устраняется стандартным способом – делением числителя и знаменателя на «эн» в старшей степени.
устраняется стандартным способом – делением числителя и знаменателя на «эн» в старшей степени.
(6) Почленно делим числители на знаменатели, и указываем слагаемые, которые стремятся к нулю.
(7) Упрощаем ответ и делаем пометку, что 
 с выводом о том, что, по признаку Даламбера исследуемый ряд сходится.
с выводом о том, что, по признаку Даламбера исследуемый ряд сходится.
В рассмотренном примере в общем члене ряда у нас встретился многочлен 2-ой степени. Что делать, если там многочлен 3-ей, 4-ой или более высокой степени? Дело в том, что если дан многочлен более высокой степени, то возникнут трудности с раскрытием скобок. В этом случае можно применять «турбо»-метод решения.
Пример 2
Возьмём похожий ряд и исследуем его на сходимость

Сначала полное решение, потом комментарии:
Используем признак Даламбера:

Таким образом, исследуемый ряд сходится.
(1) Составляем отношение 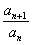 .
.
(2) Избавляемся от четырехэтажности дроби.
(3) Рассмотрим выражение  в числителе и выражение
в числителе и выражение  в знаменателе. Мы видим, что в числителе нужно раскрывать скобки и возводить в четвертую степень:
в знаменателе. Мы видим, что в числителе нужно раскрывать скобки и возводить в четвертую степень:  , чего делать совершенно не хочется. Кроме того, для тех, кто не знаком с биномом Ньютона, данная задача вообще может оказаться невыполнимой. Проанализируем старшие степени: если мы вверху раскроем скобки
, чего делать совершенно не хочется. Кроме того, для тех, кто не знаком с биномом Ньютона, данная задача вообще может оказаться невыполнимой. Проанализируем старшие степени: если мы вверху раскроем скобки 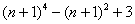 , то получим старшую степень
, то получим старшую степень 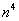 . Внизу у нас такая же старшая степень:
. Внизу у нас такая же старшая степень: 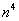 . По аналогии с предыдущим примером, очевидно, что при почленном делении числителя и знаменателя на
. По аналогии с предыдущим примером, очевидно, что при почленном делении числителя и знаменателя на 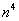 у нас в пределе получится единица. Или, как говорят математики, многочлены
у нас в пределе получится единица. Или, как говорят математики, многочлены 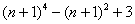 и
и 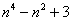 – одного порядка роста. Таким образом, вполне можно обвести отношение
– одного порядка роста. Таким образом, вполне можно обвести отношение  простым карандашом и сразу указать, что эта штука стремится к единице. Аналогично расправляемся со второй парой многочленов:
простым карандашом и сразу указать, что эта штука стремится к единице. Аналогично расправляемся со второй парой многочленов:  и
и  , они тоже одного порядка роста, и их отношение стремится к единице.
, они тоже одного порядка роста, и их отношение стремится к единице.
На самом деле, такую «халтуру» можно было провернуть и в Примере №1, но для многочлена 2-ой степени такое решение смотрится всё-таки как-то несолидно. Лично я поступаю так: если есть многочлен (или многочлены) первой или второй степени, я использую «длинный» способ решения Примера 1. Если попадается многочлен 3-ей и более высоких степеней, я использую «турбо»-метод по образцу Примера 2.
Пример 3
Исследовать ряд на сходимость 
В общий член ряда входит и степень, и факториал. Ясно, как день, что здесь надо использовать признак Даламбера. Решаем.

Таким образом, исследуемый ряд расходится.
(1) Составляем отношение 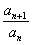 . Повторяем еще раз. По условию общий член ряда:
. Повторяем еще раз. По условию общий член ряда:  . Для того чтобы получить следующий член ряда, вместо
. Для того чтобы получить следующий член ряда, вместо  нужно подставить
нужно подставить  , таким образом:
, таким образом: 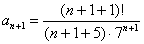 .
.
(2) Избавляемся от четырехэтажности дроби.
(3) Отщипываем семерку от степени. Факториалы расписываем подробно. Как это сделать – см. начало урока или статью о числовых последовательностях.
(4) Сокращаем всё, что можно сократить.
(5) Константу  выносим за знак предела. В числителе раскрываем скобки.
выносим за знак предела. В числителе раскрываем скобки.
(6) Неопределенность  устраняем стандартным способом – делением числителя и знаменателя на «эн» в старшей степени.
устраняем стандартным способом – делением числителя и знаменателя на «эн» в старшей степени.
Пример 5
Исследовать ряд на сходимость 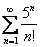
Полное решение и образец оформления в конце урока
Пример 6
Исследовать ряд на сходимость 
Иногда встречаются ряды, которые в своей начинке содержат «цепь» множителей, этот тип ряда мы еще не рассматривали. Как исследовать ряд с «цепочкой» множителей? Использовать признак Даламбера. Но сначала для понимания происходящего распишем ряд подробно:

Из разложения мы видим, что у каждого следующего члена ряда добавляется дополнительный множитель в знаменателе, поэтому, если общий член ряда 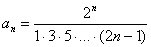 , то следующий член ряда:
, то следующий член ряда:
 . Вот здесь часто автоматом допускают ошибку, формально по алгоритму записывая, что
. Вот здесь часто автоматом допускают ошибку, формально по алгоритму записывая, что 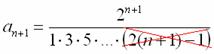
Примерный образец решения может выглядеть так:
Используем признак Даламбера:

Таким образом, исследуемый ряд сходится.
|
из
5.00
|
Обсуждение в статье: Практическая работа№ 7 |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

